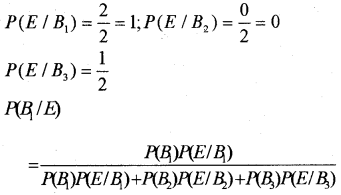Kerala Plus Two Maths Model Question Paper 1 with Answers
| Board | SCERT |
| Class | Plus Two |
| Subject | Maths |
| Category | Plus Two Previous Year Question Papers |
Time : 2½ Hours
Cool off time : 15 Minutes
Maximum : 80 Score
General Instructions to Candidates :
- There is a ‘Cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘Cool off time’ to get familiar with questions and to plan your answers.
- Read questions carefully before you answering.
- Read the instructions carefully.
- When you select a question, all the sub-questions must be answered from the same question itself.
- Calculations, figures and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non programmable calculators are not allowed in the Examination Hall.
Questions 1 to 7 carry 3 Scores each. Answer any six questions only. (6 × 3 = 18)
Question 1.
i) Let R be a relation on the set {1, 2, 3} given by R = {(1, 1), (2, 2), (1, 2), (2, 1), (2, 3)}. Which among the following element to be included to R so that R becomes Symmetric?
a) (3, 3)
b) (3, 2)
c) (1, 3)
d) (3, 1)
ii) If * is defined by a*b = a – b2 and \(\oplus\) is defined by a \(\oplus\) b = a2 + b , where a and b are integers. Then find the value of (3 \(\oplus\) 4) * 5
Answer:
i) b) (3, 2)
ii) (3 \(\oplus\) 4) * 5 = (32 + 4) * 5
= 13 * 5
= 13 – 52 = -12
Question 2.
If X + Y = \(\left[\begin{array}{ll}
5 & 2 \\
0 & 9
\end{array}\right]\) and X – Y = \(\left[\begin{array}{cc}
3 & 6 \\
0 & -1
\end{array}\right]\)find 2X – 3Y.
Answer:
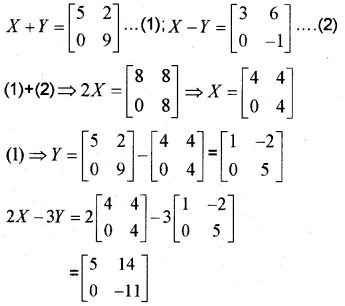
Question 3.
Find rate of change of area of a circle.
a) with respect to the radius, when r = 10cm
b) with respect to the time when the radius is increasing at the rate of 0.7 cm/s. Given that r = 5cm
Answer:
i) Area of a circle A = πr2
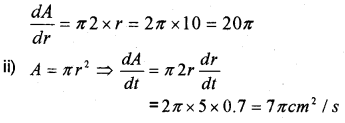
Question 4.
i) Integrate \(\int \frac{(1+\log x)^{2}}{x} d x\)
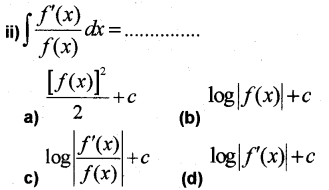
Answer:
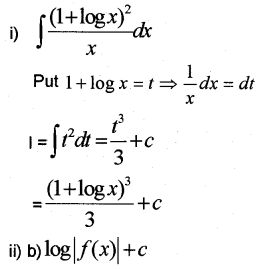
Question 5.
Find the area of a circle with centre (0, 0) and radius ‘a’ using integration.
Answer:
Equation of the circle is x2 + y2 = a2
y = \(\sqrt{a^{2}-x^{2}}\)
Area of the circle will 4 time the area under the curve from 0 to a.
Area = \(4 \int_{0}^{a} y d x=4 \int_{0}^{a} \sqrt{a^{2}-x^{2}} d x\)
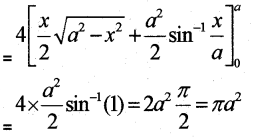
Question 6.
Consider the differential equation \(\frac{d y}{d x}=\frac{x+y}{x}\)
i) Write the order of the differential equation.
ii) Solve the above given differential equation.
Answer:
i) Order = 1.

Question 7.
Following table shows a brief description about manufacturing process of a company. Time required in hours per unit of the product and maximum availability of machine is also given in the table:
| Product | Time required in hours/Unit on machine | Profit per Unit in Rupees | |
| Machine G | Machine H | ||
| A | 3 | 5 | 20 |
| B | 4 | 6 | 30 |
| Maximum available time 10 hrs/day | Maximum available time 15 hrs/day | ||
i) Write the objective function.
ii) Whether it is a maximization case or a minimization case. Justify.
iii) Write the constraints.
Answer:
Let x units = Machine G and y units = Machine H
i) Objective function: Z = 20x + 30y
ii) It is a maximization problem.
iii) Constraints are:
3x + 4y ≤ 10; 5x + 6y ≤ 15; x, y ≥ 0
Questions 8 to 17 carry 4 scores each. Answer any 8 questions. (8 × 4 = 32)
Question 8.
i) A function f : A → B, where A = {1, 2, 3} and B = {4, 5, 6} defined by f(1) = 5, f(2) = 6, f(3) = 4, Check whether f is a bijection. If it is a bijection, write f-1 as set of ordered pair.
ii) The operation table for an operation * is given below. Given that 1 is the identity element. Then which among the following is true regarding the element in the first column?
| * | 1 | 2 | 3 |
| 1 | 2 | 3 | |
| 2 | 2 | 3 | |
| 3 | 3 | 3 |
a) 3, 2, 2
b) 1, 2, 3
c) 1, 1, 2
d) 2, 2, 2
Check whether * is commutative.
Answer:
i) A = {1, 2, 3}; B = {4, 5, 6}
f(1) = 5, f(2) = 6, f(3) = 4
Hence f= {(1, 5),(2, 6),(3, 4)}
f-1 = {(5, 1), (6, 2), (4, 3)}
ii) b) 1, 2, 3
Since; 1*2 = 2 and 2*1 =2
3 * 2 = 3 and 2*3 = 3
Therefore * is commutative
Question 9.
i) If Sin-1 x = y, then
(a) 0 ≤ y ≤ π
b) \(-\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\)
c) 0 < y < π
d) \(-\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\)
ii) Find the principal value of sin-1 (\(\frac{1}{2}\))
iii) sin-1x = \(\frac{3}{4}\) find the value of cos-1 x
Answer:
i) \(-\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\)
ii) sin-1 \(\frac{1}{2}\) = \(\frac{\pi}{6}\)
iii) sin-1x + cos-1x = \(\frac{\pi}{2}\)
\(\frac{3}{4}\) + cos-1x = \(\frac{\pi}{2}\) ⇒ cos-1x = \(\frac{\pi}{2}\) – \(\frac{3}{4}\)
Question 10.
i) Find the relation between ‘a’ and ‘b’ so that the function defined by
f(x) = \(\left\{\begin{array}{ll}
a x+1, & x \leq 3 \\
b x+3, & x>3
\end{array}\right.\) is continuous at x = 3
ii) “All continuous function are not differentiable.” Justify your answer with an example.
Answer:
i) Since f(x) is continuous at x = 3
\(\lim _{x \rightarrow 3^{-}}\) f(x) = \(\lim _{x \rightarrow 3^{+}}\) f(x) = f(3)
\(\lim _{x \rightarrow 3}\) (ax + 1) = \(\lim _{x \rightarrow 3}\) (bx + 3) = 3a +1
⇒ 3a + 1 = 3b + 3 = 3a +1
⇒ 3a + l = 3b + 3 ⇒ 3a – 3b – 2 = 0
ii) Consider the function f(x) = |x|.
Let us check the continuity and differentiability at x = 0.

Left derivative * Right derivative
Therefore not differentiable at x = 0.
Question 11.
i) Find the equation to the tangent to the curve y = x2 – 2x + 7 at (2, 7)
ii) Find the maximum value of the function?
Answer:
f(x) = sin x + cos x, 0 < x < \(\frac{\pi}{2}\)
i) y = x2 – 2x + 7 ⇒ \(\frac{d y}{d x}\) = 2x – 2
Slope at x = 2 is 2 × 2 – 2 – 2
Equation of the tangent is
(y – y1) = m(x – x1)
⇒ (y – 7) = 2(x- 2)
⇒ y – 7 = 2x – 4
⇒ 2x – y + 3 = 0
ii) c) f(x) = sin x + cos x
f'(x) = cos x – sin x
f”(x) = -sinx-cosx
For turning points;
f'(x) = cos x – sin x = 0 ⇒ tan x = 1
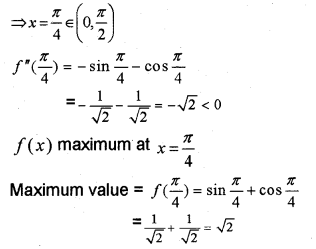
Question 12.
Integrate \(\int \frac{x+2}{2 x^{2}+6 x+5} d x\)
Answer:
Put x + 2 = A(4x + 6) + B
4A = 1 ⇒ A = \(\frac{1}{4}\)
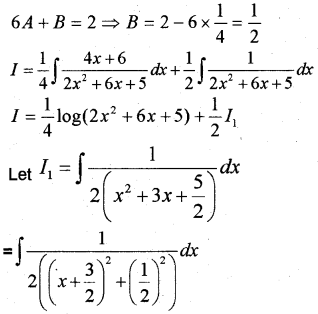

Question 13.
Consider the differential equation
x \(\frac{d y}{d x}\) + y = \(\frac{1}{x^{2}}\)
i) Find the integrating factor.
ii) Solve the above differential equation.
Answer:

Question 14.
lf the vectors \(\overline{P Q}\) = -3i + 4j + 4k and \(\overline{P R}\) = -5i + 2j + 4k are the sides of a ΔPQR
i) Find the angle between \(\overline{P Q}\) and \(\overline{P R}\)
ii) Find the length of the median through the vertex P.
Answer:
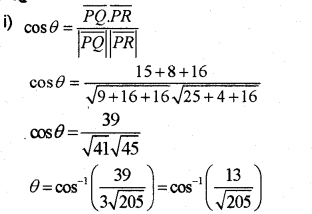
ii)
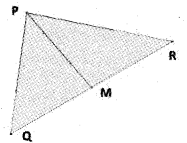
With respect to the initial P the position vector of Q and R will be \(\overline{P Q}\) = -3i + 4j + 4k
and \(\overline{P R}\) = -5i + 2j + 4k respectively.
Since M is the midpoint of QR. The position vector of M will be

Question 15.
i) If \(\bar{a}\) = 5i – j – 3k and \(\bar{b}\) = i + 3j + 5k, then show that the vectors \(\bar{a}+\bar{b}, \bar{a}-\bar{b}\) are perpendicular.
ii) If \(\bar{a}\) = i – 2j + 3k, \(\bar{b}\) = 2i + 3j – 4k and
\(\bar{c}\) = i – 3j + 5k, then check whether \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) are coplanar.
Answer:

Question 16.
i) Find the Cartesian equation of the line passing through origin and (5, -2, 3) ii) The point P(x, y, z) lies in the first octant and its distance from the origin is 12 units. If the position vector of P makes angles 45°, 60°with x and y axes respectively, find coordinates of P.
Answer:

Since P lies in the first octant, we take n = \(\frac{1}{2}\)
Therefore the coordinate of P is
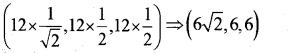
Question 17.
Solve graphically Maximise Z = 5x + 3y Subject to the constraints 3x + 5y ≤ 15; 5x + 2y ≤ 10; x ≥ 0, y ≥ 0.
Answer:
In the figure the shaded region OABC is the fesible region. Here the region is bounded.
The corner points are
O(0, 0), A(2, 0), B(\(\frac{20}{19}, \frac{45}{19})\), C(0, 3)
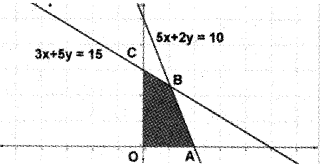
Given Z = 5x + 3y
| Corner points | Value of Z |
| O | Z = 0 |
| A | Z = 5(2) + 3(0) = 10 |
| B | Z = \(5\left(\frac{20}{19}\right)+3\left(\frac{45}{19}\right)=\frac{235}{19}\) |
| C | Z = 5(0) + 3(3) = 9 |
Since maximum value of Z occurs at B, the soluion is z = \(\frac{235}{19}\), (\(\frac{20}{19}\), \(\frac{45}{19}\))
Questions 18 to 24 carry 6 scores each. Answer any 5 questions. (5 × 6 = 30)
Question 18.
A = \(\left[\begin{array}{ccc}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\)
a) Find AT
b) Express A as the sum of a symmetric and skew symmetric matrix.
ii) If AT = \(\left[\begin{array}{cc}
\cos x & \sin x \\
-\sin x & \cos x
\end{array}\right]\), verift that AT A = I
Answer:

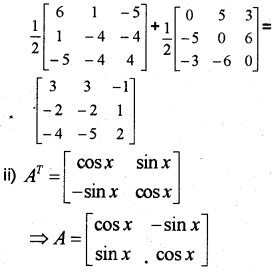
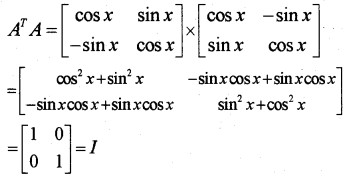
Question 19.
i) Without expanding prove that
\(\left|\begin{array}{ccc}
x+y & y+z & z+x \\
z & x & y \\
1 & 1 & 1
\end{array}\right|\) = 0
ii) Consider the following system of equations
2x – 3y + 5z = 11; 3x + 2y – 4z = -5; x + y – 2z = -3
a) Express the system in Ax = B form.
b) Solve the system by matrix method.
Answer:
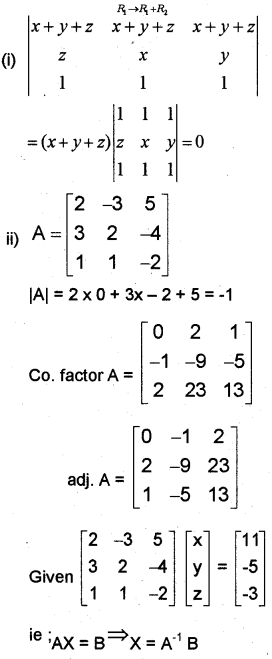
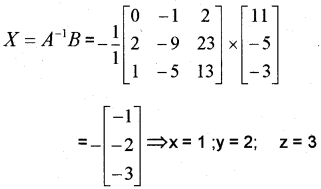
Question 20.
Find \(\frac{d y}{d x}\) of the following
i) x2 + 2xy + 2y2 = 1
ii) yx = 2x
iii) x = cos θ; y = sin θ at θ = \(\frac{\pi}{4}\)
Answer:
i) x2 + 2xy + 2y2 = 1
Differentiating w.r.to x;
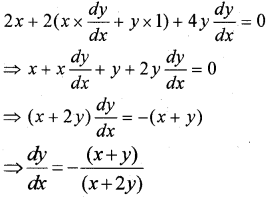
ii) yx = 2x
Take log on both sides;
x log y = x log 2
Differentiating w.r.to x;
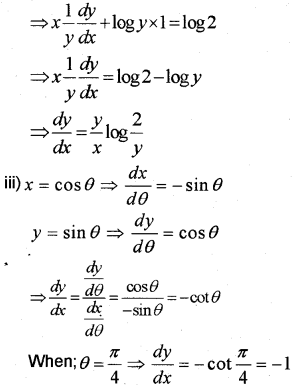
Question 21.
Evaluate the following
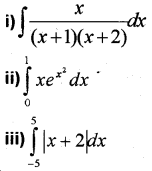
Answer:
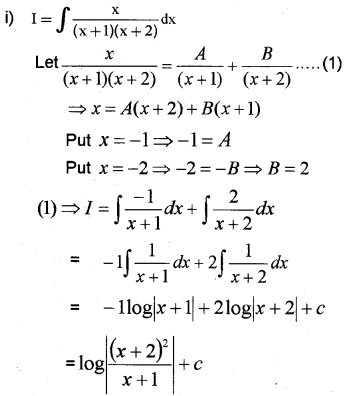
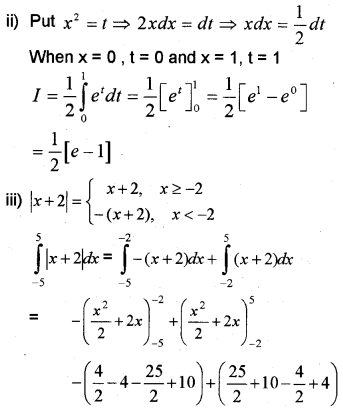
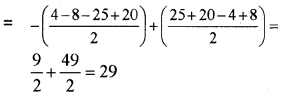
Question 22.
Consider the parabolas y2 = 4x, x2 = 4y
i) Draw a rough figure for the above parabolas.
ii) Find the point of intersection of the two parabolas.
iii) Find the area bounded by these two parabolas.
Answer:
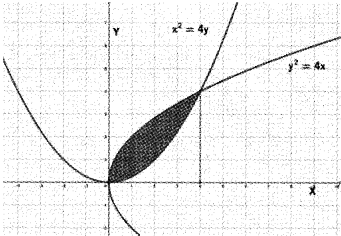
ii) solving the two conics we get the point of intersection as (0, 0) and (4, 4).
iii) Area of the enclosed region
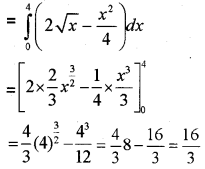
Question 23.
i) Find the shortest distance between the lines whose vector equations are
\(\bar{r}\) = (i + 2j + 3k) + λ(i – 3j + 2k) and \(\bar{r}\) =(4i + 5j + 6k) + μ(i – 3j + 2k)
ii) If a plane meets positive x axis at a distance of 2 units from the origin, positive y axis at a distance of 3 units from the origin and positive z axis at a distance of 4 units from the origin. Find the equation of the plane.
iii) Find the perpendicular distance of (0, 0, 0) from the plane obtained in part (ii)
Answer:
i) \(\overline{a_{1}}\) = i + 2j + 3k; \(\bar{b}\) = i – 3j + 2k
\(\overline{a_{2}}\) = 4i + 5j + 6k Both lines are parallel.


Question 24.
i) A die is thrown twice let the event A be ‘odd number on first throw’ and B be ‘odd number on the second throw’ check whether A and B are independent.
ii) Coloured balls are distributed in three boxes as shown in the following table:
| Box | Red | Black |
| 1 | 2 | 0 |
| II | 0 | 2 |
| III | 1 | 1 |
A box is selected at random and a ball is taken out. If the ball taken is of red colour, What is the probability that the other ball in the box is also of red colour?
Answer:
i) n(S) = 36
A = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
B = {(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3), (1, 5), (2, 5), (3,5), (4, 5), (5, 5), (6, 5)}
(A ∩ B) = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)}
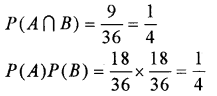
Therefore A and B are independent.
ii) Let B1, B2, B3 are the event of getting the boxes.
P(B1) = P(B2) = P(B3) = \(\frac{1}{3}\)
Let E be the event of getting a red ball.