Plus Two Maths Chapter Wise Questions and Answers Chapter 11 Three Dimensional Geometry are part of Plus Two Maths Chapter Wise Questions and Answers. Here we have given Plus Two Maths Chapter Wise Questions and Answers Chapter 11 Three Dimensional Geometry
.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Chapter Wise Questions |
| Chapter | Chapter 11 |
| Chapter Name | Three Dimensional Geometry |
| Number of Questions Solved | 41 |
| Category | Kerala Plus Two |
Kerala Plus Two Maths Chapter Wise Questions and Answers Chapter 11 Three Dimensional Geometry
Plus Two Maths Three Dimensional Geometry Three Mark Questions and Answers
Question 1.
![]()
- Write the Cartesian equation. (1)
- Find the angle between the line. (2)
Answer:
1.
![]()
2. cosθ
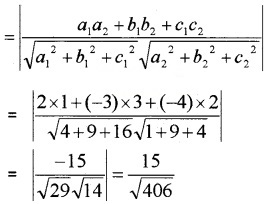
Question 2.
Find the vector equation of the plane passing through the intersection of the planes \(\bar{r}\).(i + j + k) = 6 and \(\bar{r}\).(2i + 3 j + 4k) = -5 at the point (1,1,1).
Answer:
The Cartesian equation of the planes are x + y + z = 6 and 2x + 3y + 4z = – 5. Therefore the equation of the plane passing through the intersection of these planes is
x + y + z – 6 + k(2x + 3y + 4z + 5) = 0
Since it pass through (1, 1, 1) we get,
1 + 1 + 1 – 6 + k(2 + 3 + 4 + 5) = 0 ⇒ -3 + k14 ⇒ k = \(\frac{3}{14}\)
∴ the equation is
x + y + z + -6 + \(\frac{3}{14}\) (2x + 3 y + 4z + 5) = 0
14x + 14y + 14z – 84 + 6x + 9y + 12z + 15 = 0
20x + 23y + 26z = 69
Vector equation is \(\bar{r}\). (20i + 23j + 26k) = 69.
Question 3.
Find the equation of the plane passing through the intersection of the planes x + y + 4z + 5 = 0 and 2x – y + 3z + 6 = 0 and contains the point (1, 0, 0).
Answer:
The equation of the planes passing through the intersection of the planes
x + y + 4z + 5 = 0 and 2x – y + 3z + 6 = 0 is
x + y + 4z + 5 + k(2x – y + 3z + 6) = 0 ____(1)
Since (1) pass through (1, 0, 0)
⇒ 1 + 0 + 0 + 5 + k(2 – 0 + 0 + 6) = 0
⇒ 6 + 8k = 0 ⇒ k = –\(\frac{3}{4}\); Then (1)
⇒ x + y + z + 5 + \(\frac{3}{4}\)(2x – y + 3z + 6) = 0
⇒ 4x + 4y + 16z + 20 – 6x + 3y – 9z – 18 = 0
⇒ 2x – 7y – 7z = 2.
Plus Two Maths Three Dimensional Geometry Four Mark Questions and Answers
Question 1.
Consider the point (-1, -2, -3).
- In which octant, the above point lies.(1)
- Find the direction cosines of the line joining (-1, -2, -3) and (3, 4, 5). (1)
- If P is any point such that OP = \(\sqrt{50}\) and direction cosines of OP are \(\frac{3}{\sqrt{50}}\), \(\frac{4}{\sqrt{50}}\) and \(\frac{5}{\sqrt{50}}\), then find the co-ordinate of P. (2)
Answer:
1. The point lies in the octant X’OY’Z’.
2. Direction ratios of the line joining (-1, -2, -3) and (3, 4, 5) are (3 + 1), (4 + 2), (5 + 3) ⇒ 4, 6, 8 ⇒ 2, 3, 4.
Therefore direction cosines are
![]()
3. Given, OP = \(\sqrt{50}\)

Therefore the point is (3, 4, 5).
Question 2.
Consider a cube of side ‘a’ unit has one vertex at the origin O.

- Write down the co-ordinate of 0, 0′, A and A’ (1)
- Find the direction ratios of OO’ and AA’. (2)
- Show that the angle between the main diagonals of the above cube is cos-1\(\left(\frac{1}{3}\right)\) (1)
Answer:
1. O(0, 0, 0), O'(a, a, a), A(a, 0, 0) and A'(0, a, a).
2. Direction ratios along OO’ is a – 0, a – 0, a – 0
⇒ a, a ,a ⇒ 1, 1, 1
3. cosθ

Question 3.
Consider two points A and B and a line L as shown in the figure.

- Find \(\overline{A B}\) (1)
- Find the Cartesian equation of the line L. (1)
- Find the foot of the perpendicular drawn from ( 2, 3, 4 ) to the line L. (2)
Answer:
1. \(\overline{A B}\) = (3 – 1)i + (- 3 – 3)j + (3 – 0)k = 2i – 6j + 3k.
2. The Cartesian equation of a line passing through the point (4, 0, -1 ) and parallel to the vector \(\overline{A B}\) is
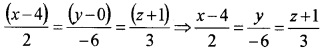
3. We take, \(\frac{x-4}{2}=\frac{y}{-6}=\frac{z+1}{3}\) = r then any point of the line can be taken as (2r + 4, -6r, 3r – 1). Assume that this point be the foot of the perpendicular drawn from (2, 3, 4 ). The dr’s of the line is 2 : – 6 : 3 and dr’s of the perpendicular line L is
2r + 4 – 2 : -6r – 3 : 3r – 1 – 4 ⇒ 2r + 2: -6r – 3 : 3r – 5
Since perpendicular,
2(2 r + 2) – 6(-6 r -3) + 3(3r – 5) = 0
49r = -7 ⇒ r = \(\frac{-7}{49}\) = –\(\frac{1}{7}\). Therefore the foot of the
perpendicular is
![]()
Question 4.
Cartesian equation of two lines are
![]()
(i) Write the vector equation of the lines. (2)
(ii) Shortest distance between the lines. (2)
Answer:
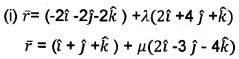

Question 5.
Consider the points (1, 3, 4) & (-3, 5, 2)
- Find the equation of the line through P and Q. (1)
- At which point that the above line cuts the plane 2x + y + z + 3 = 0. (3)
Answer:
1. Equation of a line passing through( 1, 3, 4) and (-3, 5, 2) is given by,
![]()
![]()
2. Let \(\frac{x-1}{-2}=\frac{y-3}{1}=\frac{z-4}{-1}\) = λ
Then any point on the line is (-2λ + 1, λ + 3, -λ + 4)
Since the plane 2x + y + z + 3 = 0 cuts the aboveline. We have,
⇒ 2(-λ + 1) + λ + 3 – λ + 4 + 3 = 0
⇒ -2λ + 2 + λ + 3 – λ + 4 + 3 = 0
⇒ -2λ = -12 ⇒ λ = 6
∴ point of intersection is (-2 × 6 + 1, 6 + 3, -6 + 4)
⇒ (-11, 9, -2).
Question 6.
Let the equation of a plane be \(\bar{r}\). (2i – 3j + 5k) = 7, then
- Find the Cartesian equation of the plane. (1)
- Find the equation of a plane passing through the point (3, 4, -1) and parallel to the given plane. (2)
- Find the distance between the parallel planes. (1)
Answer:
1. Given, \(\bar{r}\).(2i – 3j + 5k) = 7 and if we substitute \(\bar{r}\) = xi + yj + zk Then we get the Cartesian equation as 2x – 3y + 5z – 7 = 0.
2. The equation of a plane parallel to the above plane differ only by a constant, therefore let the equation be 2x – 3y + 5z + k = 0.
⇒ 6 – 12 – 5 + k = 0 ⇒ k = 11
Therefore the equation is 2x – 3y + 5z + 11 = 0
3. The distance between the parallel planes
![]()
Question 7.
- State the condition for the line \(\bar{r}\) = \(\bar{a}\) + λ \(\bar{b}\) is parallel to the plane \(\bar{r}\).\(\bar{n}\) = d. (2)
- Show that the line \(\bar{r}\) = i + j + λ(2i + j + 4k) is parallel to the plane \(\bar{r}\). (-2i + k) = 5. (1)
- Find the distance between the line and The Plane in (ii). (1)
Answer:
1. The line \(\bar{r}\) = \(\bar{a}\) + λ \(\bar{b}\) is parallel to the plane \(\bar{r}\).\(\bar{n}\) = d, if the normal of the plane is perpendicularto the line.
∴ \(\bar{b}\).\(\bar{n}\) = 0.
2. Given,
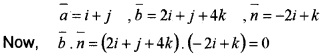
The line \(\bar{r}\) = i + j + λ(2i + j + 4k) is parallel to the plane \(\bar{r}\). (-2i + 4k) = 5 ⇒ -2x + 4y = 5.
3. Distance = Distance between – 2x + 4y = 5 and point (1, 1, 0) on the line
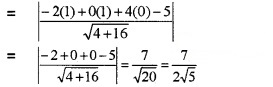
Question 8.
Choose the correct answer from the bracket,
(i) If a line in the space makes angle α, β, and γ with the coordinates axes, then cos2α + cos2β + cos2γ is equal to (1)
(a) 1
(b) 2
(c) 0
(d) 3
(ii) The direction ratios of the line are \(\frac{x-6}{1}=\frac{2-y}{2}=\frac{z-2}{2}\) (1)
(a) 6, -2, -2
(b) 1, 2, 2
(c) 6, 1, -2
(d) 0, 0, 0
(iii) If the vector equation of a line is \(\bar{r}\) = i + j + k + µ(2i – 3j – 4k), then the Cartesian equation of the line
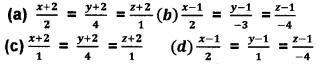
(iv) If the Cartesian equation of a plane is x + y + z =12, then the vector equation of the line is (1)
(a) \(\bar{r}\).(2i + j + k) = 12
(b) \(\bar{r}\).(i + j + k) = 12
(C) \(\bar{r}\).(i + y + 2k) = 12
(d) \(\bar{r}\).(i + 3j + k) = 12
Answer:
(i) (a) 1
(ii) (b) 1, 2, 2
(iii) (b) \(\frac{x-I}{2}=\frac{y-1}{-3}=\frac{z-1}{-4}\)
(iv) (b) \(\bar{r}\).(i + j + k) = 12.
Question 9.
Consider the lines \(\bar{r}\) = (i + 2j – 2k) + λ(i + 2 j) and \(\bar{r}\) = (i + 2j – 2k) + µ(2j – k)
- Find the angle between the lines.
- Find a vector perpendicular to both the lines.
- Find the equation of the line passing through the point of intersection of lines and perpendicular to both the lines.
Answer:
1. \(\bar{b}_{1}\) = i + 2j; \(\bar{b}_{2}\) = 2j – k

2. Perpendicular vector = \(\bar{b}_{1}\) × \(\bar{b}_{2}\)
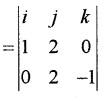
= i(-2 – 0) -j(-1 – 0) + k(2 – 0)
= -2i + j + k.
3. Equation of line is \(\bar{r}\) = (i + 2j – k) + µ(-2i + j + 2k).
Question 10.
Consider the line \(\bar{r}\) = (2i – j + k) + λ(i + 2j + 3k)
- Find the Cartesian equation of the line.
- Find the vector equation of the line passing through A (1, 0, 2) and parallel to the above line.
- Write two points on the line obtained in (ii) which are equidistant from A.
Answer:
1. \(\frac{x-2}{1}=\frac{y+1}{2}=\frac{z-1}{3}\).
2. \(\bar{r}\) = (i + 2k) + λ(i + 2j + 3k).
3. Put λ = a and λ = -a for any real value ‘a’.
Let us put λ = 1 and λ = -1
\(\bar{r}\) = (i + 2k) + 1(i + 2j + 3k) = 2i + 2j + 5k
⇒ (2, 2, 5)
\(\bar{r}\) = (i + 2k) – 1(i + 2j + 3k) = 0i – 2j – k
⇒ (0, -2, -1)
The equidistant points are(2, 2, 5) and (0, -2, -1).
Question 11.
- Find the equation of the plane through the point(1, 2, 3) and perpendicular to the plane x – y + z = 2 and 2x + y – 3z = 5 (2)
- Find the distance between the planes x – 2y + 2z – 8 = 0 and 6y – 3x – 6z = 57 (2)
Answer:
1. Required equation is
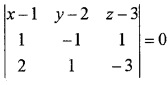
(x – 1)(3 – 1) – (y – 2)(-3 – 2) + (z – 3)(1 + 2) = 0
2(x – 1) + 5(y – 2) + 3(z – 3) = 0
2x + 5y + 3z – 2 – 10 – 9 = 0
2x + 5y + 3z – 21 = 0
2. The planes are
x – 2y + 2z – 8 = 0 and 3x – 6y + 6z + 57 = 0
ie, 3x – 6y + 6z – 24 = 0 and 3x – 6y + 6z + 57 = 0
Distance

Question 12.
Consider the Cartesian equation of a line \(\frac{x-3}{2}=\frac{y+1}{3}=\frac{z-5}{-2}\)
- Find the vector equation of the line. (1)
- Find its intersecting point with the plane 5x + 2y – 6z – 7 = 0 (2)
- Find the angle made by the line with the plane 5x + 2y – 6z – 7 = 0 (1)
Answer:
1. The vector equation is \(\bar{r}\) = (3i – j + 5k) + λ(2i + 3 j – 2k).
2. Any point on the line is
\(\frac{x-3}{2}=\frac{y+1}{3}=\frac{z-5}{-2}\) = λ
x = 2λ + 3, y = 3, λ – 1, z = -2λ + 5
Since this lies on the plane ,it satisfies the plane
5(2λ + 3) + 2(3λ – 1) -6(-2λ + 5) – 7 = 0
10λ + 6λ + 12λ + 15 – 2 – 30 – 7 = 0
28λ = 24
λ = 6/7
The point of intersection is \(\left[\frac{33}{7}, \frac{11}{7}, \frac{23}{7}\right]\).
3. Let θ be the angle between the line and the plane. The direction of the line and the plane
\(\bar{b}\) = 2i + 3j + k; \(\bar{m}\) = 5i + 2j – 6k
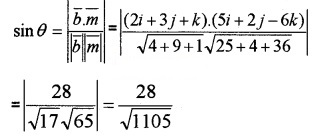
Question 13.
From the following figure
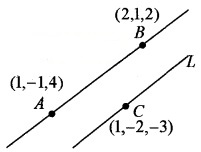
- Find \(\overline{A B}\). (1)
- Find the vector equation of line L. (1)
- Find a point on line L other than C. (2)
Answer:
1. P.v of A = i – j + 4k,
P.v. of B = 2i + j + 2k
\(\overline{A B}\) = p. v. of B – p. v. of A
= 2i + j + 2k -(i – j + 4k) = i + 2j – 2k.
2. The line L passes through (1, -2, -3) and parallel to \(\overline{A B}\)
![]()
∴ Vector equation of line L is \(\bar{r}=\bar{a}+\lambda \bar{m}\)
![]()
3. From (1) of part (ii), we have
xi + yj + zk = (l + λ)i + (-2 + 2λ)j + (-3 – 2λ)k
Put λ = 1
⇒ xi +yj + zk = (1 +1)i + (-2 + 2)j + (-3 – 2 )k
⇒ xi + yj + zk = 2i + 0j – 5k
Therefore a point on line L is (2, 0, -5).
Question 14.
Find the vector equation of the plane which is at a distance of \(\frac{6}{\sqrt{29}}\) from the origin with perpendicular vector 2i – 3j + 4k. Convert into Cartesian form. Also, find the foot of the perpendicular drawn from the origin to the Plane.
Answer:

Perpendicular distance from origin = d = \(\frac{6}{\sqrt{29}}\)
The equation of the Plane is \(\bar{r}\).\(\hat{n}\) = d

Cartesian equation is 2x – 3y + 4z = 6
The direction cosines perpendicular to the Plane is \(\frac{2}{\sqrt{29}},-\frac{3}{\sqrt{29}}, \frac{4}{\sqrt{29}}\).
Perpendicular distance to the Plane is as \(\frac{6}{\sqrt{29}}\)
Hence the foot of the perpendicular is
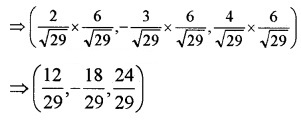
Question 15.
Consider the Plane \(\bar{r}\).(-6i -3j – 2k) + 1 = 0, find the direction cosines perpendicular to the Plane and perpendicular distance from the origin.
Answer:
Convert the equation of the plane into normal form

Direction cosines perpendicular to the Plane is \(\frac{6}{7}, \frac{3}{7}, \frac{2}{7}\)
Perpendicular distance from the origin is \(\frac{1}{7}\).
Question 16.
Consider three points (6, -1, 1), (5, 1, 2) and (1, – 5, -4) on space.
- Find the Cartesian equation of the plane passing through these points. (2)
- Find direction ratios normal to the Plane.(1)
- Find a unit vector normal to the Plane. (1)
Answer:
1. Equation of a plane passing through the points (6, -1, 1),(5, 1, 2) and (1, -5, 4)

⇒ (x – 6)(-10 + 4) – (y + 1)(5 + 5) + (z – 1)(4 + 10) = 0
⇒ (x – 6)(-6) – (y + 1)(10) + (z – 1)(14) = 0
⇒ -6x + 36 – 10y – 10 + 14z – 14 = 0
⇒ 6x +10y – 14z -12 = 0.
2. Dr’s normal to the plane are 6 : 10 : -14 ⇒ 3 : 5 : -7.
3. Since the dr’s normal to the plane are 3 : 5 : -7, a unit vector in this direction is

Question 17.
Consider a straight line through a fixed point with position vector 2i – 2j + 3k and parallel to i – j + 4k.
- Write down the vector equation of the straight line. (1)
- Show that the straight line is parallel to the plane \(\bar{r}\).(i + 5y + k) = 5 (1)
- Find the distance between the line and plane. (2)
Answer:
1. Vector equation of a straight line is \(\bar{r}=\bar{a}+\lambda \bar{b}\) where a is \(\bar{a}\) fixed point and \(\bar{b}\) is a vector parallel to the line. Here \(\bar{a}\) = 2i – 2y + 3 it and \(\bar{b}\) = i – j + 4k. Therefore vector equation of the line \(\bar{r}\) = 2i – 2j + 3k + λ(i – j + 4k).
2. The vector parallel to the line is i – j + 4k and vector normal to the plane is i + 5j + k.
Then, (i – j + 4k). (i + 5j + k) = 1 – 5 + 4 = 0
implies that straight line and plane are parallel.
3. A point on the line is 2i – 2j + 3k. Then the distance of 2i – 2j + 3k to the given plane

Question 18.
Consider the vector equation of two planes \(\bar{r}\).(2i + j + k) = 3, \(\bar{r}\).(i – j – k) = 4
- Find the vector equation of any plane through the intersection of the above two planes. (2)
- Find the vector equation of the plane through the intersection of the above planes and the point (1, 2, -1 ) (2)
Answer:
1. The cartesian equation are 2x + y + z – 3 = 0 and x – y – z – 4 = 0 Required equation of the plane is
(2x + y + z – 3) + λ(x – y – z – 4) = 0
(2+ λ)x + (1 – λ)y + (1 – λ)z + (-3 – 4λ) = 0.
2. The above plane passes through (1, 2, -1)
(2+ λ)1 + (1 – λ)2 + (1 – λ)(-1) + (-3 – 4λ) = 0
3 – 3 + 4λ = 0
λ = 0
Equation of the plane is 2x + y + z – 3 = 0
\(\bar{r}\).(2i + j + k) = 3.
Question 19.
(i) Distance of the point(0, 0, 1) from the plane x + y + z = 3
(a) \(\frac{1}{\sqrt{3}}\) units
(b) \(\frac{2}{\sqrt{3}}\) units
(c) \(\sqrt{3}\) units
(d) \(\frac{\sqrt{3}}{2}\) units
(ii) Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to x – y + z = 0 (3)
Answer:
(i) (b) \(\frac{2}{\sqrt{3}}\) units.
(ii) Equation of the plane passing through the intersection is of the form
x + y + z – 1 + λ(2x + 3y + 4z – 5) = 0 _____(1)
(1 + 2λ)x + (1 + 3λ)j + (1 + 4λ)z – 1 – 5λ = 0
Thr Dr’s of the required plane is
(1 + 2λ), (1 + 3λ), (1 + 4λ)
Thr Dr’s of the Perpendicular plane is 1, -1, 1
⇒ (1 + 2λ)(1) + (1 + 3λ)(-1) + (1 + 4λ)(1) = 0
⇒ 1 + 2λ – 1 – 3λ + 1 + 4λ = 0
⇒ 3λ + 1 = 0 ⇒ λ = \(\frac{-1}{3}\)
(1) ⇒ x + y + z – \(\frac{1}{3}\)(2x + 3y + 4z – 5) = 0
⇒ 3x + 3y + 3z – 2x – 3y – 4z + 5 = 0
⇒ x – z + 2 = 0.
Question 20.
Consider a plane \(\bar{r}\).(6i – 3j – 2k) + 1 = 0
- Find dc’s perpendicular to the plane. (2)
- Find a vector of magnitude 14 units perpendicular to given plane. (1)
- Find the equation of a line parallel to the above vector and passing through the point (1, 2, 1 ). (1)
Answer:
1. Given, \(\bar{r}\).(6i – 3j – 2k) + 1 = 0 ____(1)
Now, |6i – 3j – 2k| = \(\sqrt{36+9+4}\) = 7
∴ \(\frac{6}{7} i-\frac{3}{7} j-\frac{2}{7} k\) is a unit perpendicular to the plane (1)
⇒ the dc’s perpendicular to the plane (1) are \(\frac{6}{7},-\frac{3}{7},-\frac{2}{7}\).
2. We have, \(\frac{6}{7} i-\frac{3}{7} j-\frac{2}{7} k\) is a unit perpendicular to the Plane (1). Therefore, a vector of magnitude 14 units perpendicular to the Plane (1) is 14(\(\frac{6}{7} i-\frac{3}{7} j-\frac{2}{7} k\))
⇒ 12i – 6j – 4k.
3. Equation of a line parallel to the vector 12i – 6j – 4k and passing through the point (1, 2, 1 )is given by
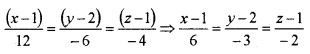
Plus Two Maths Three Dimensional Geometry Six Mark Questions and Answers
Question 1.
Consider the pair of lines whose equations are
![]()
- Write the direction ratios of the lines. (1)
- Find the shortest distance between the above skew lines. (4)
- Find the angle between these two lines. (1)
Answer:
1. The direction ratios are 2, 5, – 3 and – 1, 8, 4.
2. The given lines are \(\bar{r}\) = (2i + j – 3k) + λ(2i + 5j – 3k)
i.e. \(\bar{r}\) = \(\overline{a_{1}}+\lambda \overline{b_{1}}\),
where \(\overline{a_{1}}\) = 2i + j – 3k) + λ(2i + 5j – 3k)
and \(\bar{r}\) =(-i + 4j + 5k) + µ(-i + 8j + 4k)
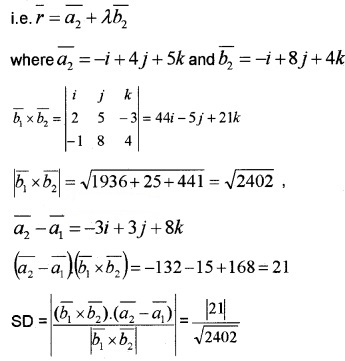
3. cosθ

Question 2.
Consider the pair of lines \(\bar{r}\) = 3i + 4j – 2k + λ(-i + 2j + k) ——L1, \(\bar{r}\) = i – 7j – 2k + µ(i + 3j + 2k) ——L2
- Find one point each on lines L1 and L2. (1)
- Find the distance between those points. (2)
- Find the shortest distance between L1 and L2. (3)
Answer:
1. By putting λ = 0 in line L1 and µ = 0 in L2 we get the required points. L1 ⇒ \(\bar{r}\) = 3i + 4j – 2k
∴ Co-ordinate is (3, 4, -2)
L2 ⇒ \(\bar{r}\) = i – 7j – 2k
∴ Co-ordinate is (1, -7, -2).
2. Distance between (3, 4, -2) and (1, -7, -2)
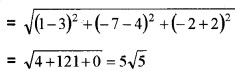
3. Let L1 ⇒ \(\bar{r}\) = 3i + 4j – 2k + λ(-i + 2j + k) is of the form \(\bar{r}=\overline{a_{1}}+\lambda \overline{b_{1}}\) where
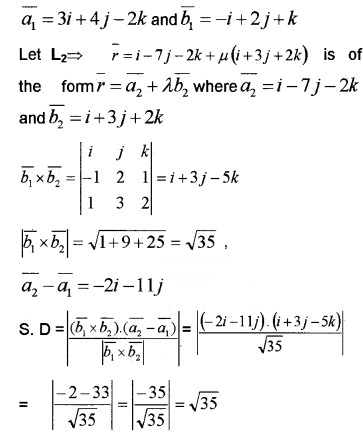
Question 3.
Consider the points A (2, 2, -1), B (3, 4, 2) and C (7, 0, 6).
- Are A, B, and C collinear? Explain.
- Find the vector and Cartesian equation of the plane passing these three points. (2)
- Find the angle between the above plane and the line \(\bar{r}\) = (i + 2j – k) + λ(i – j + k) (2)
Answer:
1. Direction ratios along A and B is 3 -2, 4 -2, 2 + 1 ⇒ 1, 2, 3
Direction ratios along B and C is
7 -3, 0 -4, 6 -2 ⇒ 4, -4, 4
Since the direction ratios are not proportional they are not collinear.
2. Cartesian equation of the Plane is
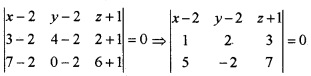
⇒ (x – 2)(14 + 6) -(y – 2)(7 – 15) + (z + 1)(-2 -10) = 0
⇒ 20(x – 2) + 8(y – 2) – 12(z + 1) = 0
⇒ 20x – 40 + 8y – 16 – 12z – 12 = 0
⇒ 20x + 8y – 12z = 68
⇒ 5x + 2y – 3z = 17
Vector Equation is \(\bar{r}\).(5i + 2j – 3k) = 17.
3. Angle between the Plane and the Line
\(\bar{r}\) = (i + 2j – k) + λ(i – j + k)
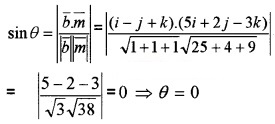
Question 4.
Consider three points on space ( 2, 1, 0 ), (3, -2, -2)and(3, 1, 7)
- Find the Cartesian equation of the plane passing through the above points. (2)
- Convert the above equation into vector form.
- Hence, find a unit vector perpendicular to the above plane and also find the perpendicular distance of the plane from the origin. (2)
Answer:
1. Equation of the plane is

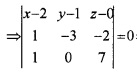
⇒ (x – 2)(-21) – (y – 1)(7 + 2) + z(0 + 3) = 0
⇒ 21x + 42 – 9y + 9 + 3z = 0 ⇒ -21x – 9y + 3z + 51 = 0
⇒ 7x + 3y – z = 17.
2. Vector form is \(\bar{r}\).(7i + 3j – k) = 17 _____(1)
3. Now, |7i + 3j – k| = \(\sqrt{49+9+1}=\sqrt{59}\)
Dividing equation (1) by \(\sqrt{59}\), we get
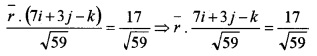
Therefore the above equation is the normal form of the plane. Then \(\frac{7 i+3 j-k}{\sqrt{59}}\) is the unit vector perpendicular to the plane and \(\frac{17}{\sqrt{59}}\) is the perpendicular distance from the origin.
Question 5.
\(\overline{O A}\) = i + 2j + 3k
\(\overline{O B}\) = i – 2j + 4k
\(\overline{O C}\) = 2i + 3j + k
are adjacent sides of the parallelopiped.
- Find the base area of the parallelopiped. (2)
(Base determined by \(\overline{O A}\) and \(\overline{O B}\)) - Find the volume of the parallelopiped. (2)
- Find the height of the parallelopiped. (2)
Answer:
1. \(\overline{O A}\) × \(\overline{O B}\) =
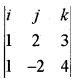
= 14i – j – 4k
Base area = |l4i – j – 4k|
\(=\sqrt{196+1+16}=\sqrt{213}\)
2. Volume of the parallelopiped is
![]()
= (14i – j – 4k).(2i + 3 j + k)
= 28 – 3 – 4 = 21.
3. Height = \(\frac{\text {volume}}{\text {base area}}=\frac{21}{\sqrt{213}}\).
Question 6.
- Find the equation of the line passing through the point (2, 1, 0) and (3, 2, -1) (3)
- Find the shortest distance of the above line from the line \(\bar{r}\) = (i – j + 2k) + λ(2i + j – 3k) (3)
Answer:
1.

2.
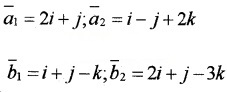

= i(-3 + 1) – j(-3 + 2) + k(1 – 2)
= -2i + j – k
Question 7.
The equation of two lines are
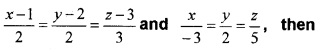
- Find the dr’s of the given lines. (2)
- Find the angle between the given lines. (2)
- Find the equation of the line passing through (2, 1, 3) and perpendicular to the given lines. (2)
Answer:
1. The given lines are
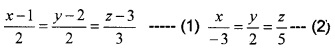
The dr’s of (1) are 2, 2, 3 and dr’s of (2) are -3, 2, 5.
2. The angle between (1) and (2) is given by

3. Let a, b, c be the dr’s of the line perpendicular to lines (1) and (2).
∴ 2a + 2b + 3c = 0, -3a + 2b + 5c = 0
Solving by the rule of cross-multiplication, we get

∴ dr’s of the required line are 4, -19, 10 and the line passes through (2, 1, 3).
∴ Equation of the required line is
\(\frac{x-2}{4}=\frac{y-1}{-19}=\frac{z-3}{10}\).
Question 8.
- Find the direction cosines of the vector 2i + 2j – k. (1)
- Find the distance of the point (2, 3, 4) from the plane \(\bar{r}\).(3i – 6j + 2 k) = -11. (2)
- Find the shortest distance between the lines \(\bar{r}\) = (2i – j – k)+ λ(3i – 5 j + 2k) an \(\bar{r}\) = (i+ 2 j + k)+ µ(i – j + k) (3)
Answer:
1. Direction ratios of the vector 2i + 2j – k is 2, 2, -1
Direction cosines of the vector 2i + 2j – k is
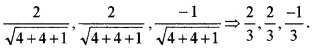
2. The equation of the plane in the Cartesian form is 3x – 6y + 2z + 11 = 0 . Then distance from the point (2, 3, 4) is

3. The given lines are \(\bar{r}\) = (2i – j – k) + λ(3i – 5j + 2k)
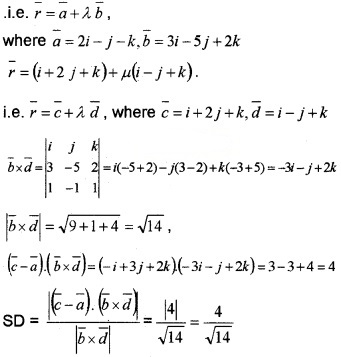
We hope the given Plus Two Maths Chapter Wise Questions and Answers Chapter 11 Three Dimensional Geometry will help you. If you have any query regarding Plus Two Maths Chapter Wise Questions and Answers Chapter 11 Three Dimensional Geometry, drop a comment below and we will get back to you at the earliest.