Plus Two Maths Chapter Wise Questions and Answers Chapter 10 Vector Algebra are part of Plus Two Maths Chapter Wise Questions and Answers. Here we have given Plus Two Maths Chapter Wise Questions and Answers Chapter 10 Vector Algebra.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Chapter Wise Questions |
| Chapter | Chapter 10 |
| Chapter Name | Vector Algebra |
| Number of Questions Solved | 48 |
| Category | Kerala Plus Two |
Kerala Plus Two Maths Chapter Wise Questions and Answers Chapter 10 Vector Algebra
Plus Two Maths Vector Algebra Three Mark Questions and Answers
Question 1.
Find \(\bar{a}+\bar{b}, \bar{a}-\bar{b}\) and \(\bar{b}+\bar{c}\) using the vectors.
\(\bar{a}\) = 3i + 4j + k, \(\bar{b}\) = 2i – 7 j – 3k and \(\bar{c}\) = 2i + 3j – 9k.
Answer:
\(\bar{a}+\bar{b}\) = 3i + 4j + k + 2i – 7j – 3k = 5i – 3j – 2k
\(\bar{a}-\bar{b}\) = 3i + 4j + k – (2i – 7j -3k) = i + 11j + 4k
\(\bar{b}+\bar{c}\) = 2i – 7j -3k + 2i +3j – 9k
= 4i – 4j – 12k.
Question 2.
- Find the vector passing through the point A( 1, 2, -3) and B(-1, -2, 1).
- Find the direction cosines along with AB.
Answer:
1. \(\overline{A B}\) = \(\overline{O B}\) – \(\overline{O A}\) = -i – 2j + k – (i + 2j – 3k) = -2i – 4j + 4k.
2. Unit Vector
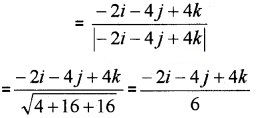
Direction cosines are \(\frac{-2}{6}\), \(\frac{-4}{6}\), \(\frac{4}{6}\).
Question 3.
Show that the points A, B and C with position vectors \(\bar{a}\) = 3i – 4j – 4k, \(\bar{b}\) = 2i – j + k and \(\bar{c}\) = i – 3j – 5k respectively from the vertices of a right angled triangle.
Answer:
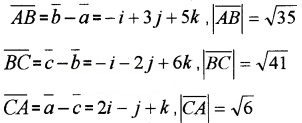
41 = 35 + 6 ⇒ BC2 = AB2 + CA2
Hence right angled triangle.
Question 4.
Prove that \([\bar{a}+\bar{b} \bar{b}+\bar{c} \bar{c}+\bar{a}]=2[\bar{a} \bar{b} \bar{c}]\).
Answer:
LHS
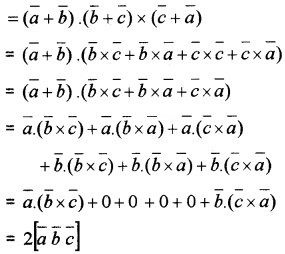
Note: If \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) are coplanar then so is \([\bar{a}+\bar{b} \bar{b}+\bar{c} \bar{c}+\bar{a}]\).
Question 5.
Consider the vector \(\bar{p}\) = 2i – j + k. Find two vectors \(\bar{q}\) and \(\bar{r}\) such that \(\bar{p}\), \(\bar{q}\) and \(\bar{r}\) are mutually perpendicular.
Answer:
Find a vector \(\bar{q}\) such that \(\bar{p} \cdot \bar{q}\) = 0, for this use any \(\bar{q}\) whose two components are randomly selected. Let \(\bar{q}\) = 2i + 2j + xk
\(\bar{p} \cdot \bar{q}\) = (2i – j + k) . (2i + 2 j + xk) = 0
⇒ 4 – 2 + x = 0 ⇒ x = -2
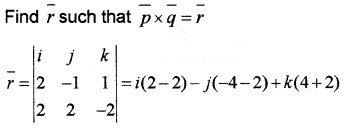
= 6j + 6k.
Question 6.
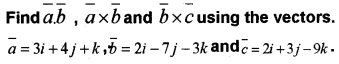
Answer:
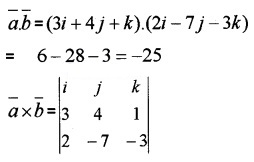
= i(-12 + 7) – j(-9 – 2) + k(-21 – 8)
= -5i + 11j – 29k
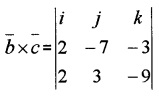
= i(63 + 9) – j(-18 + 6) + k(6 – 14)
= 72i + 12 j – 8k.
Question 7.
If \(\bar{a}\) = 3i + j + 2k,
(i) Find the magnitude of \(\bar{a}\). (1)
(ii) If the projection of \(\bar{a}\) on another vector \(\bar{b}\) is \(\sqrt{14}\), which among the following could be \(\bar{b}\) ? (1)
(a) i + j + k
(b) 6i + 2j + 4k
(c) 3i – j + 2k
(d) 2i + 3j + k
(iii) If \(\bar{a}\) makes an angle 60° with a vector \(\bar{c}\), find the projection of \(\bar{a}\) on \(\bar{c}\) (1)
Answer:
![]()
(ii) Since projection of \(\bar{a}\) on another vector \(\bar{b}\) and magnitude of \(\bar{a}\) is \(\sqrt{14}\), then \(\bar{a}\) and \(\bar{b}\) are parallel, (b) 6i + 2j + 4k.
(iii) Projection of \(\bar{a}\) on \(\bar{c}\)
= |\(\bar{a}\)|cos60° = \(\sqrt{14}\) × \(\frac{1}{2}\) = \(\frac{\sqrt{14}}{2}\).
Question 8.
(i) The projection of the vector 2i + 3j + 2k on the vector i + j + k is (1)
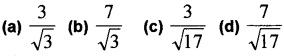
(ii) Find the area of a parallelogram whose adjacent sides are the vectors 2i + j + k and 6i – j (2)
Answer:

(ii) Let \(\bar{a}\) = 2i + j + k, \(\bar{b}\) = i – j
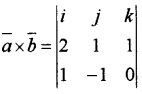
= i(0 + 1) – j(0 – 1) + k(-2 – 1 ) = i + j -3k
Area =
![]()
Question 9.
(i) The angle between the vectors i + j and j + k is (1)
(a) 60°
(b) 30°
(c) 45°
(d) 90°

Answer:
(i) (a) 60°
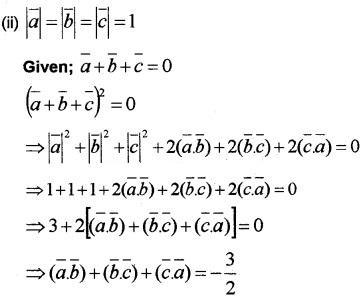
Question 10.
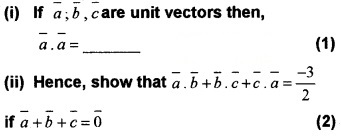
Answer:
![]()
(ii) Given, \(\bar{a}\) + \(\bar{b}\) + \(\bar{a}\) = \(\bar{0}\), squaring both sides we get
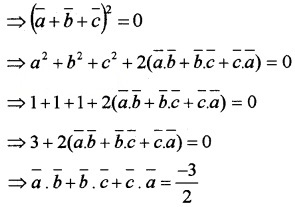
Plus Two Maths Vector Algebra Four Mark Questions and Answers
Question 1.
Let A (2, 3), B (1, 4), C (0, -2), and D (x, y) are vertices of a parallelogram ABCD.
- Write the position vectors A, B, C, and D. (2)
- Find the value of x and y. (2)
Answer:
1. Position vector of A = 2i + 3 j
Position vector of B = i + 4j
Position vector of C = 0i – 2j
Position vector of D = xi + yj.
2. Since ABCD is a parallelogram, then
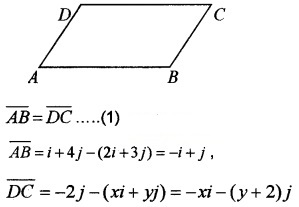
(1) ⇒ -i + j = -xi – (y + 2 )j
x = 1, -2 – y = 1 ⇒ y = -3
∴ D is (1, -3).
Question 2.
Find the position vector of a point R which divides the line joining the two points P and Q whose vectors i + 2j – k and -i + j + k in the ratio 2:1
- internally and
- externally.
Answer:
\(\overline{O P}\) = i + 2j – k, \(\overline{O Q}\) = -i + j + k
Let R be the position vector of the dividing point,
1.
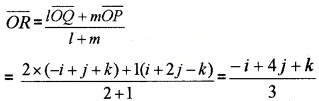
2.
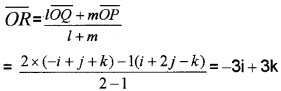
Question 3.
(i) Choose the correct answer from the bracket. If a unit vector \(\widehat{a}\) makes angles \(\frac{\pi}{4}\) with i and \(\frac{\pi}{3}\) with j and acute angle θ with k. then θ is
(a) \(\frac{\pi}{6}\),
(b) \(\frac{\pi}{4}\),
(c) \(\frac{\pi}{3}\),
(d) \(\frac{\pi}{2}\) (1)
(ii) Find a unit vector \(\widehat{a}\) (1)
(iii) Write down a unit vector in XY plane, making an angle 60°of with the positive direction of x – axis. (2)
Answer:
(i) (c), Since I = cos\(\frac{\pi}{4}\) = \(\frac{1}{\sqrt{2}}\), m = cos\(\frac{\pi}{3}\) = 1/2;
n = cos θ
l2 + m2 + n2 = 1
n2 = 1 – (\(\frac{1}{2}\))2 – (\(\frac{1}{\sqrt{2}}\))2 = 1/4
n = \(\frac{1}{2}\), cosθ = 1/2 , θ = \(\frac{\pi}{3}\).
(ii)
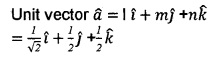
Question 4.
Let the vectors \(\bar{a}\), \(\bar{b}\), \(\bar{c}\) denoted the sides of a triangle ABC.
(i) Prove that (2)
![]()
(ii) Find the projection of the vector i + 3j + 7k on the vector 7i – j + 8k (2)
Answer:
(ii) Projection of the vector i + 3j + 7k on the vector 7i – j + 8k
Question 5.
(i) If \(\bar{a}\) and \(\bar{b}\) are any two vectors, then axb is (1)
(a) a vector on the same plane where \(\bar{a}\) and \(\bar{b}\) lie.
(b) ab cosθ, if θ is the angle between them.
(c) a vector parallel to both \(\bar{a}\) and \(\bar{b}\).
(d) a vector perpendicular to both \(\bar{a}\) and \(\bar{b}\).
(ii) Let \(\bar{a}\) = 2i + 4j – 5k, \(\bar{b}\) = i + 2j + 3k. Then find a unit vector perpendicular to both \(\bar{a}\) and \(\bar{b}\). (2)
(iii) Find a vector of magnitude 5 in the direction perpendicular to both \(\bar{a}\) and \(\bar{b}\) (1)
Answer:
(i) (d) a vector perpendicular to both \(\bar{a}\) and \(\bar{b}\).
(ii) \(\bar{a}\) = 2i + 4j-5k, \(\bar{b}\) = i + 2j+3k
= i(12 + 10) – j(6 + 5) + k(4 – 4) = 22i – 11j
![]()
Therefore unit vector perpendicular to both \(\bar{a}\) and \(\bar{b}\) is
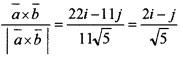
(iii) 5 × unit vector perpendicular to both \(\bar{a}\) and \(\bar{b}\)
![]()
Question 6.
Consider a vector that is inclined at an angle 45° to x-axis and 60° to y-axis
- Find the dc’s of the vector. (2)
- Find a unit vector in the direction of the above vector. (1)
- Find a vector which is of magnitude 10 units in the direction of the above vector. (1)
Answer:
1. Let l, m, n are the direction ratios.
Given that, l = cos 45° = \(\frac{1}{\sqrt{2}}\), m = cos 60° = \(\frac{1}{2}\)
⇒ l2 + m2 + n2 = 1
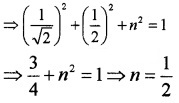
∴ the dc’s of the vector are \(\frac{1}{\sqrt{2}}\), \(\frac{1}{2}\), \(\frac{1}{2}\)
2. A unit vector in the direction of the above vector is given by li + mj + nk ⇒ \(\frac{1}{\sqrt{2}}\)i + \(\frac{1}{2}\)j + \(\frac{1}{2}\)k.
3. A vector, which is of magnitude 10 units in the direction of the above vector is given by
![]()
Question 7.
Consider the point A(2, 1, 1) and B(4, 2, 3)
- Find the vector \(\overline{A B}\) (1)
- Find the direction cosines of \(\overline{A B}\) (2)
- Find the angle made by \(\overline{A B}\) with the positive direction of x-axis. (1)
Answer:
1. \(\overline{A B}\) = 2i + j + 2k
2. |\(\overline{A B}\)| = \(\sqrt{4+1+4}\) = 3
The direction cosines are \(\frac{2}{3}\), \(\frac{1}{3}\), \(\frac{2}{3}\).
3. cos α = \(\frac{2}{3}\) ⇒ α = cos-1(\(\frac{2}{3}\)).
Question 8.
If i + j + k, 2i + 5j, 3i + 2 j – 3k, i – 6j – k respectively are the position vector of points A, B,C and D. Then
- Find \(\overline{A B}\) and \(\overline{C D}\). (1)
- Find the angle between the vectors \(\overline{A B}\) and \(\overline{C D}\). (2)
- Deduce that \(\overline{A B}\) parallel to \(\overline{C D}\). (1)
Answer:
1.
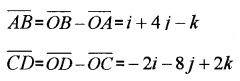
2.
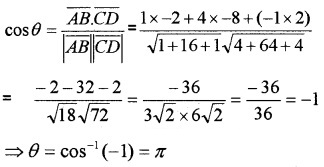
3. Since the angle between \(\overline{A B}\) and \(\overline{C D}\) is π they are parallel.
Question 9.
Let ABCD be a parallelogram with sides as given in the figure.
- Find area of the parallelogram. (2)
- Find the distance between the sides AB and DC. (2)
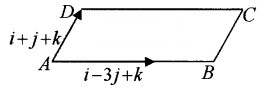
Answer:
1. Given;
\(\overline{A B}\) = i – 3j + k and \(\overline{A D}\) = i + j + k
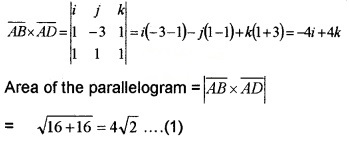
2. Let h be the distance between the parallelsides AB and DC. Then ; Area = Base × h _____(2)
Here, Base = |\(\overline{A B}\)|
|i – 3j + k| = \(\sqrt{1+9+1}=\sqrt{11}\)
From (1) and (2)
![]()
Question 10.
Consider \(\bar{a}\) = i + 2j – 3k, \(\bar{b}\) = 3i – j + 2k, \(\bar{c}\) = 11i + 2j
- Find \(\bar{a}\) + \(\bar{b}\) and \(\bar{a}\).\(\bar{b}\) (2)
- Find the unit vector in the direction of \(\bar{a}\) + \(\bar{b}\). (1)
- Show that \(\bar{a}\) + \(\bar{b}\) and \(\bar{a}\) – \(\bar{b}\) are orthogonal. (1)
Answer:
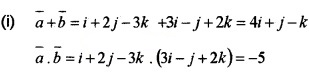
(ii) Unit vector in the direction of
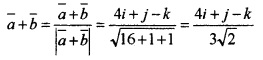
(iii) We have,

Therefore, they are orthogonal.
Question 11.
Let A (1, -1, 4), B ( 2, 1, 2 ) and C (1, -2, -3 )
- Find \(\overline{A B}\). (1)
- Find the angle between \(\overline{A B}\) and \(\overline{A C}\).(2)
- Find the area of the parallelogram formed by \(\overline{A B}\) and \(\overline{A C}\) as adjacent sides. (1)
Answer:
1. \(\overline{A B}\) = P.v of B – P.v of A
= 2 i + j + 2 k – (i – j + 4k) = i + 2 j – 2k
2. \(\overline{A C}\) = P.v of C – P.v of A
= i – 2 j – 3 k -(i – j + 4k) = – j – 7k
Let A be the angle between \(\overline{A B}\) and \(\overline{A C}\)
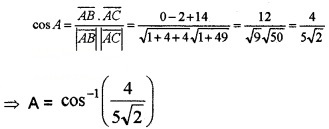
3.
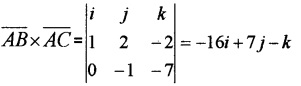
Area of the parallelogram
![]()
Plus Two Maths Vector Algebra Six Mark Questions and Answers
Question 1.
Using this figure answer the following questions.
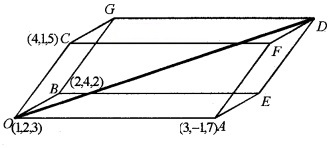
- Find \(\overline{O A}\), \(\overline{O B}\), \(\overline{O C}\) (2)
- Find \(\overline{O D}\) (2)
- Find the coordinate of the vertex D. (2)
Answer:
1. \(\overline{O A}\) = (3 – 1)i + (-1 – 2)j + (7 – 3)k = 2i – 3j + 4k
\(\overline{O B}\) = (2 – 1)i + (4 – 2)j +(2 – 3)k = i + 2j – k
\(\overline{O C}\) = (4 – 1)i + (1 – 2 )j + (5 – 3 )k = 3i – j + 2 k.
2. From the figure,
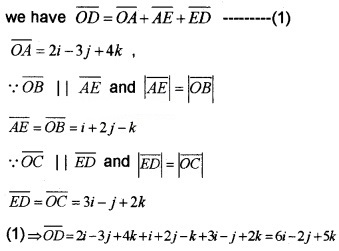
3. Let the vertex of D be (x , y , z),
Then, \(\overline{O D}\) = (x – 1)i + (y – 2)j + (z – 3)k.
But we have,
\(\overline{O D}\) = 6i – 2j + 5k = (x – 1)i + (y – 2)j +(z – 3)k
x – 1 = 6 ⇒ x = 7, y – 2 = -2 ⇒ y = 0, z – 3 = 5 ⇒ z = 8.
Question 2.
OABCDEFG is a cube with edges of length 8 units and axes as shown. L, M, N are midpoints of the edges FG, GD, GB respectively.
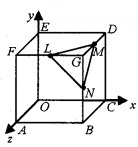
- Find p.v’s of F, B,D and G. (1)
- Show that the angle between the main diagonals is θ = cos-1\(\left(\frac{1}{3}\right)\). (2)
- Find the p.v’s of L, M, N. (1)
- Show that \(\overline{L M}+\overline{M N}+\overline{N L}=0\). (1)
Answer:
1. \(\overline{O F}\) = 8 j + 8k, \(\overline{O B}\) = 8i + 8k, \(\overline{O D}\) = 8i + 8k, \(\overline{O G}\) = 8i + 8j + 8k.
2. Consider the main diagonals \(\overline{O G}\) and \(\overline{E B}\)
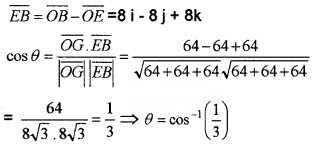
3. P.V of L = \(\overline{O L}\) = 4i + 8j + 8k
P.V of M = \(\overline{O M}\) = 8i + 8j + 4k
P.V of N = \(\overline{O N}\) = 8i + 4j + 8k
4.
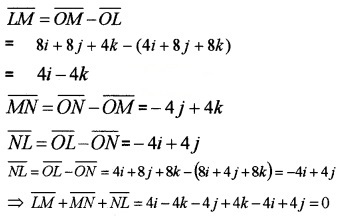
Question 3.
Using the figure answer the following questions
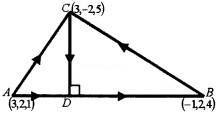
- Evaluate \(\overline{A B}\).\(\overline{A C}\) (2)
- Find \(\overline{A D}\) . (2)
- Find the coordinates of D.
Answer:
1. \(\overline{A B}\) = p.v of B – p.v of A= -4i + 0j + 3k
\(\overline{A C}\) = p.v of C – p.v of A = 0i – 4 j + 4k
\(\overline{A B}\).\(\overline{A C}\) = -4 × 0 + 0 × -4 + 3 × 4 = 12
2.

3. Let the coordinate of D be (x, y ,z)
⇒ \(\overline{A D}\) = (x – 3)i + (y – 2)j + (z – 1)k,
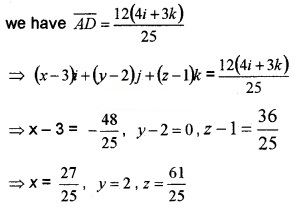
Question 4.
Consider the Parallelogram ABCD

- Find \(\overline{A B}\) and \(\overline{A D}\) (1)
- Find the area of the parallelogram ABCD. (1)
- Find \(\overline{A C}\). (2)
- Find co-ordinate of C. (2)
Answer:
1. \(\overline{A B}\) = p.v of B – p. v of A
= 3i + 5j + 8k – (i + 2j + k) = 2i + 3j + 7k
\(\overline{A D}\) = p.v of D – p. v of A
= i + 3j + 2k – (i + 2j + k)= 0i + j + k.
2.
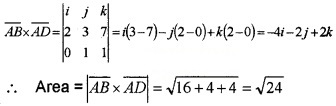
3. By triangle inequality;

4. Let the co-ordinate of C be (x, y, z)
Then, \(\overline{A C}\) = (x – 1)i + (y – 2)j + (z – 1)k = 2i + 4j + 8k
x – 1 = 2 ⇒ x = 3, y – 2 = 4 ⇒ y = 6,
z – 1 = 8 ⇒ z = 9
Co-ordinate of C is (3, 6, 9).
Question 5.
Consider the following quadrilateral ABCD in which P, Q, R, S are the midpoints of the sides.
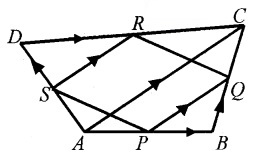
- Find \(\overline{P Q}\) and \(\overline{S R}\) in terms of \(\overline{A C}\) (2)
- Show that PQRS is a parallelogram. (2)
- If \(\bar{a}\) is any vector, prove that (2)
![]()
Answer:
1. Using triangle law of addition, we get
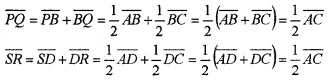
2. From the above explanation we have,
![]()
and parallel. Similarly, |\(\overline{S P}\)| = |\(\overline{R Q}\)|
Therefore, PQRS is a parallelogram.
3. Let \(\bar{a}\) = a1 i + a2 j + a3 k
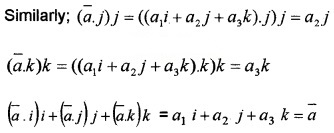
We hope the given Plus Two Maths Chapter Wise Questions and Answers Chapter 10 Vector Algebra will help you. If you have any query regarding Plus Two Maths Chapter Wise Questions and Answers Chapter 10 Vector Algebra, drop a comment below and we will get back to you at the earliest.