Plus Two Maths Chapter Wise Previous Questions Chapter 12 Linear Programming are part of Plus Two Maths Chapter Wise Previous Year Questions and Answers. Here we have given Plus Two Maths Chapter Wise Previous Chapter 12 Linear Programming.
Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 12 Linear Programming
Plus Two Maths Linear Programming 4 Marks Important Questions
Question 1.
Consider the linear programming problem;
Maximise; Z = x +y , 2x + y – 3< 0, x – 2y + 1 < 0, y < 3, x < 0, y < 0
(i) Draw its feasible region.
(ii) Find the corner points of the feasible region.
(iii) Find the corner at which Z attains its maximum. (March – 2012)
Answer:
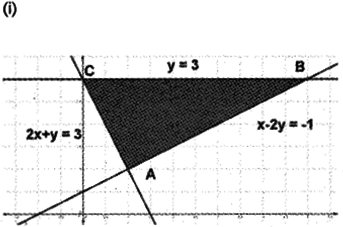
(ii) In the figure the shaded region ABC is the feasible region. Here the region is bounded. The corner points are A(1, 1), B(5, 3), C(O, 3).
(iii) Given; Z = x + y
| Corner points | Value of Z |
| A | Z = (l)+(1) = 2 |
| B | Z = (5)+(3) = 8 |
| C | Z = (0)+(3) = 3 |
Since maximum value of Z occurs at B, the soluion is Z = (5) + (3) = 8.
Question 2.
Consider the LPP Minimise; Z = 200 k + 500y, x + 2y > 10, 3x + 4y < 24, x > 0, y > 0
(i) Draw the feasible region.
(ii) Find the co-ordinates of the comer points of the feasible region.
(iii) Solve the LPP. (May – 2012)
Answer:
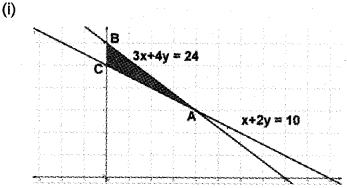
(ii) In the figure the shaded region ABC is the fesible region. Here the region is bounded. The corner points are 4(4, 3), 5(0, 6), C(0, 5)
(iii) Given; Z = 200x + 500y
| Corner points | Value of Z |
| A | Z = 200(4)+500(3) = 2300 |
| B | Z = 200(0)+500(6) = 3000 |
| C | Z = 200(0)+500(5) = 2500 |
Since minimum value of Z occurs at A, the soluion is Z = 200(4) + 500(3) = 2300.
Question 3.
Consider the LPP
Maximise; Z = 5x + 3y
Subject to; 3x + 5y < 15, 5x + 2y < 10x, y > 0
(i) Draw the feasible region.
(ii) Find the corner points of the feasible region.
(iii) Find the corner at which Z attains its maximum. (March – 2013)
Answer:
In the figure the shaded region OABC is the fesible region. Here the region is bounded.
The corner points are
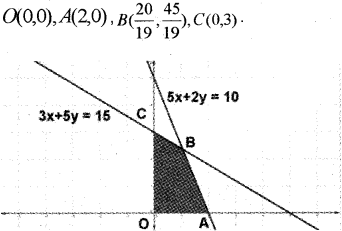
Given; Z = 5x + 3y
| Corner points | Value of Z |
| O | Z = 0 |
| A | Z = 5(2)+3(0) = 10 |
| B | \(Z=5\left(\frac{20}{19}\right)+3\left(\frac{45}{19}\right)=\frac{235}{19}\) |
| C | Z = 5(0)+3(3) = 9 |
Since maximum value of Z occurs at B, the soluion is Z =
Question 4.
Consider the linear programming problem: Minimize Z = 3x + 9y Subject to the constraints: x + 3y < 60 x + y > 10, x < y, x > 0, y > 0
(i) Draw its feasible region.
(ii) Find the vertices of the feasible region
(iii) Find the minimum value of Z subject to the given constraints. (March-2014, SAY-2016)
Answer:
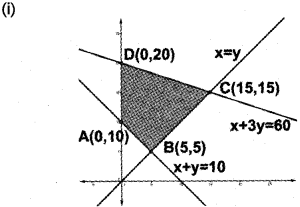
(ii) The feasible region is ABCD.
Solving x + y = 10, x = y we get B(5, 5)
Solving x + 3y = 60, x = y we get C(15, 15)
Hence the comer points are A(0, 10) , B(5, 5), C(15, 15), D(0, 20)
(iii) Given; Z = 3x + 9y
| Corner points | Value of Z |
| A | Z = 3(0)+9(10) = 90 |
| B | Z = 3(5)+9(5) = 60 |
| C | Z = 3(15)+ 9(15) = 190 |
| D | Z = 3(0)+9(20) = 180 |
Form the table, minumum value of Z is 6Oat B(5, 5).
Question 5.
Consider the linear inequalities 2x + 3y < 6; 2x + y < 4; x, y < 0
(a) Mark the feasible region.
(b) Maximise the function z = 4x + 5y subject to the given constraints. (March – 2014)
Answer:
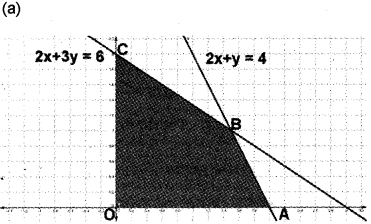
(b) 15.2x + 3y = 6
| X | 0 | 2 |
| Y | 4 | 0 |
2x + y = 4
| X | 0 | 3 |
| Y | 2 | 0 |
| Corner points | z = 4x + 5y |
| 0(0,0) | z = 0 |
| A(2,0) | 8 + 0 = 8 |
| B(1.5, 1) | 6 + 5 = 11 |
| C(0, 2) | 0 + 10 = 10 |
Maximum atx= 1.5, y 1
Maximum value is Z = 11
Question 6.
Consider the linear programming problem: Minimise Z = 4x + 4y Subject to x + 2y < 8; 3x + 2y < 12x, y<0
(a) Mark its feasible region.
(b) Find the comer points of the feasible region.
(c) Find the corner at which Z attain its minimum. (May – 2014)
Answer:
(a) x + 2y = 8,
| X | 0 | 8 |
| y | 4 | 0 |
3x + 12y = 12
| X | 0 | 4 |
| y | 6 | 0 |
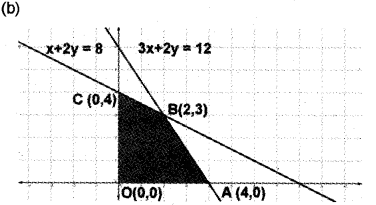
The comer points are 0(0, 0), A(4, 0), B(2, 3), C(0, 4)
(c)
| Corner point | Z = -3x+4y |
| 0 (0, 0) | Z = 0 + 0 = 0 |
| A (4,0) | Z = -12 + 0 = -12 |
| B (2, 3) | Z = -6 + 12 = 6 |
| C (0, 4) | Z = 0+ 16= 16 |
Z attains minimum at (4, 0).
Question 7.
Consider the linear programming problem: Maximum z = 4x + y
Subject to constraints: x + y < 50, 3x + y < 9x, y < 0
(a) Draw the feasible region
(b) Find the corner points of the feasible region
(c) Find the corner at which ‘z’ aftains its maximum value. (May – 2015)
Answer:
(a) x + y = 50,
| X | 0 | 50 |
| y | 50 | 0 |
3x + y = 90
| X | 0 | 30 |
| y | 90 | 0 |
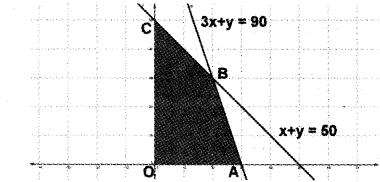
(b) Solving the equations we get the points as
O(0, 0) A(30, 0); B(20, 30); C(0, 50)
(c)
| Vertices | Z |
| 0(0,0) | 0 |
| A(30,0) | 120 maximum |
| B(20,30) | 110 |
| C(0,50) | 50 |
Z attains maximum at A(30, 0)
Question 8.
Consider the LPP
Maximise z = 3x + 2y
Subject to the constraints: x + 2y < 10, 3x + y < 15; x, y < 0
(a) Draw its feasible region
(b) Find the corner points of the feasible region
(c) Find the maximum value of Z. (March – 2016)
Answer:
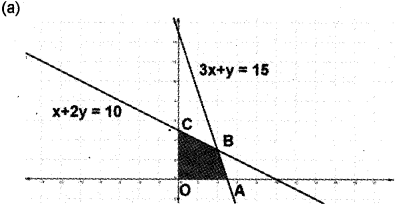
(b) The corner points 0(0,0), A(5,0), B(4,3), C(0, 5)
Z is maximum at B(4, 3), z = 18.
(c)
| o | (0,0) | Z = 3(0)+ 2(0) = 0 |
| A | (5,0), | Z= 3(5)+ 2(0) = 15 |
| B | (4,3), | Z= 3(4)+ 2(3) = 18 |
| C | (0,5) | Z= 3(0) + 2(5) = 10 |
Question 9.
Consider the linear programming problem: Maximum z = 50x + 40y
Subject to constraints:
x + 2y < 10; 3x + 4y < 24; x, y < 0
(i) Draw the feasible region
(ii) Find the comer points of the feasible region
(iii) Find the maximum value of z. (March – 2017)
Answer:
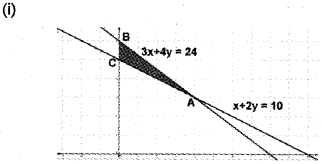
(ii) In the figure the shaded region ABC is the fesible region. Here the region is bounded. The corner points are A(4, 3), B(0,6), C(0, 5)
(iii) Given; Z = 50x + 40y
| Corner points | Value of Z |
| A | Z = 50(4)+ 40(3) = 320 |
| B | Z= 50(0)+ 40(6) = 240. |
| C | Z= 50(0)+ 40(5) = 200 |
Since minimum value of Z occurs at A, the soluion is Z = 50(4) + 4(3) = 320.
Plus Two Maths Linear Programming 6 Marks Important Questions
Question 1.
A furniture dealer sells only tables and chairs. He has Rs. 12,000 to invest and a space to store 90 pieces. A table costs him Rs. 400 and a chair Rs. 100. He can sell a table at a profit of Rs. 75 and a chair at a profit of Rs. 25. Assume that he can sell all the items. The dealer wants to get maximum profit.
(i) By defining suitable variables, write the objective function.
(ii) Write the constraints.
(iii) Maximise the objective function graphically. (March – 2010)
Answer:
(i) Let x be the number of Tables and y be the number of Chairs. Then; Maximise; z = 75x + 25y
(ii) Furniture constraints x + y < 90
Investment constraint 400x + 100y < 12000
Therefore;Maximise; Z = 75x + 25y, x + y < 90, 4x + y < 120, x<0, y<0
(iii) In the figure the shaded region OABC is the fesible region. Here the region is bounded. The corner points are O(0, 0), A(30, 0) B(10, 80), C(0, 90).
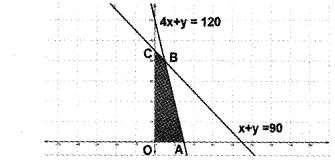
Given; Z = 75x + 25y
| Corner points | Value of Z |
| O | Z =75(0) +25(0) = 0 |
| A | Z= 75(30)+ 25(0) = 2250 |
| B | Z= 75(10)+ 25(80) = 2750 |
| C | Z= 75(0)+ 25(90) = 2250 |
Since minimum value of Z occurs at B, the soluion is Z = 2750.
Question 2.
A company produces two types of cricket balls A and B. The production time of one ball of type B is double the type A (time in units). The company has the time to produce a maximum of 2000 balls per day. The supply of raw materials is sufficient for the production of 1500 balls (both A and B) per day. The company wants to make maximum profit by making profit of Rs. 3 from a ball of type A and Rs. 5 from type B.
Then,
(i) By defining suitable variables write the objective function.
(ii) Write the constraints.
(iii) How many balls should be produced in each type per day in order to get maximum profit? (May – 2010)
Answer:
(i) Let x be the number of balls of type A and y be the number of balls of type B. Then; Maximise profit ¡s; Z = 3x + 5y
(ii) Balls constraints 2x + y < 2000 investment constraint x + y < 1500
Therefore; Maximise; Z = 3x + 5y, 2x + y < 2000, x + y < 1500, x<0, y<0
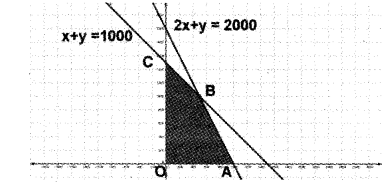
(iii) In the figure the shaded region OABC is the fesible region. Here the region ¡s bounded. The corner points are O(0, 0), A(1000, 0) B(500, 1 000), C(0, 1500). Given; Z = 3x + 5y
| Comer points | Value of Z |
| O | Z = 3(0)+ 5(0) = 0 |
| A | Z = 3(1000) + 5(0) = 3000 |
| B | Z= 3(500)+ 5(1000) = 6500 |
| C | Z= 3(0) + 5(1500) = 7500 |
Since maximum value of Z occurs at C, the soluion is Z = 3(0) + 5(1500) = 7500.
Question 3.
The graph of a linear programming problem is given below. The shaded region ¡s the feasible region. The objective function is Maximise; Z = px + qy
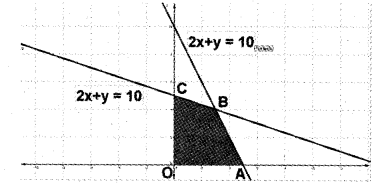
(i) What are the co-ordinates of the corners of feasible region?
(ii) Write the constraints.
(iii) If the Max. Z occurs at A and B, what ¡s the relation between p and q?
(iv) If q = 1, write the objective function.
(v) Find the Max. Z. (March – 2011)
Answer:
(i) From the figure the feasible region is OABC.
Then the comer points are;
A is (5,0), 8 is (3,4), C is (0,5) and 0 (0,0)
(ii) The constraints are 2x + y < 10, x + 3y < 15, x < 0, y<0
(iii) Given; Z = px + qy
| Corner points | Value of Z |
| O | Z=p(0)+q(0) = 0 |
| A | Z = p(5) + q(Q) = 5p |
| B | Z = p( 3)+g(4) = 3p+4q |
| C | Z = p(0)+q(5) = 5q |
Since maximum at A and B we have;
⇒ 3p + 4q = 5p ⇒ 2p = 4q ⇒ p = 2q
(iv) When q = 1, then p ⇒ 2q ⇒ p = 2
Objective function is; Z = 2x + y
(v) We have; Z px + qy at B Z has maximum ⇒ Z = 2(3) + 4 = 10
Question 4.
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and I hour on machine B to produce a package of bolts. He earns a profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. How many package of each should be produced each day so as to maximise his profit, if he produced each day so as to maximise the profit, if he operates his machines for at the most 12 hours a days?
(i) By suitable defining the variables write the objective function of the problem.
(ii) Formulate the problem as a linear programming problem(LPP)
(iii) Solve the LPP graphically and find the number of packages of nuts and bolts to be manufactured. (May -2011)
Answer:
(i) Let x be the number of packages of nuts produced and y be the number of packages of bolts produced. Then;
Maximise profit is; Z = 17. 5x + 7y
(ii) Time constraint for Machine A; x + 3y < 12
Time constraint for Machine B; 3x + y < 12
Therefore; Maximise; Z = 17.5x + 7y, x + 3y < 12, 3x + y < 12, x < 0, y < 0
(iii) In the figure the shaded region OABC is the fesible region. Here the region is bounded. The corner points are 0(0,0), A (4, 0) B(3, 3), C(0, 4).
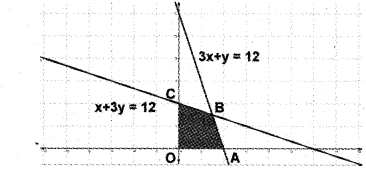
Given; Z = 17.5x + 7y
| Comer points | Value of Z |
| O | Z =17.5(0) +7(0) = 0 |
| A | Z =17.5(4)+ 7(0) = 70 |
| B | Z= 17.5(3)+ 7(3) = 73.5 |
| C | Z= 17.5(0)+7(4) = 28 |
Since maximum value of Z occurs at B, the soluion is Z = 17.5(3) + 7(3) = 73.5.
Question 5.
A bakery owner makes two types of cakes A and B. Three machines are needed for this purpose. The time (in minutes) required for making each type of cakes in each machine is given below;
| Machine | Types of cakes | |
| 1 | 12 | 6 |
| II | 18 | 0 |
| III | 6 | 9 |
Each machine is available for atmost 6 hours per day. Assume that all cakes will be sold out every day. The bakery owner wants to make maximum profit per day by making Rs. 7.5 from type A and Rs. 5 from type B.
(i) Write the objective function by defining suitable variables.
(ii) Write the constraints.
(iii) Find the maximum profit graphically. (May- 2013, EDUMATE – 2017)
Answer:
(i) Number of cake of type A: x
Number of cake of type B: y
Then profit function is Maximise: Z = 75x + 5y
(ii) 12x + 6y < 360; 18x + 0y < 360
6x + 9y < 360; x > 0, y > 0
Simplifying we get;
2x – i – y < 60………..(1)
x < 20………..(2)
2x + 3y < 120………..(3)
x > 0, y > 0
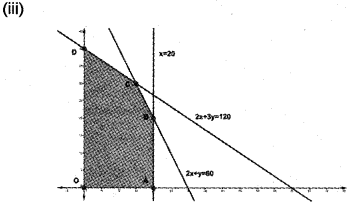
The feasible region is OABCDO
Solving (1) and (2) we get the point B- (2020)
Solving (1) and (3) we get the point C- (15,30)
A-(20,0), O-(0,0), D-(0,40)
Given; Z = x + y
| Corner points | Value of Z |
| O | Z = 7.5(0) +5(0) = 0 |
| A | Z =150 |
| B | Z = 250 |
| C | Z =112.5 |
| D | Z = 200 |
Since maximum value of Z occurs at B, the soluion is Z = 250 (20, 20).
Question 6.
In factory, there are two machines A and B producing toys. They respectively produce 60 and 80 units in one hour. A can run a maximum of 10 hours and B a maximum of 7 hours a day. The cost of their running per hour respectively amount to 2,000 and 2,500 rupees. The total duration of working these machines cannot exceed 12 hours a day. If the total cost cannot exceed Rs. 25,000 per day and the total daily production is at least 800 units, then formulate the problem mathematically. (March – 2014)
Answer:
Let x be the running time for machine A and y be the running time for machine B.
Since machines cannot work more than 12 hours x + y < 12
Since maximum production of two machines is 800 units.
60x + 80y < 800
Maximum cost of production is 25000, 2000x + 2500y < 25000
0 < x < 10, 0 < y < 7
We hope the Plus Two Maths Chapter Wise Previous Questions Chapter 12 Linear Programming help you. If you have any query regarding Kerala Plus Two Maths Chapter Wise Previous Questions Chapter 12 Linear Programming, drop a comment below and we will get back to you at the earliest.