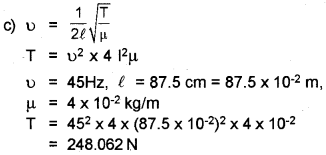Kerala Plus One Physics Previous Year Question Paper March 2018 with Answers
| Board | SCERT |
| Class | Plus One |
| Subject | Physics |
| Category | Plus One Previous Year Question Papers |
Time: 2 Hours
Cool off time: 15 Minutes
Maximum: 60 Scores
General Instructions to candidates:
- There is a ‘cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read the instructions carefully.
- Read questions carefully before you answering.
- Calculations, figures, and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non-programmable calculators are not allowed in the Examination Hall.
Answer any four questions from question numbers 1 to 5. Each carry one score. (4 × 1 = 4)
Question 1.
The branch of Physics that was developed to understand and improve the working heat engines is ………
a) Optics
b) Thermodynamics
c) Electronics
d) Electrodynamics
Answer:
b) Thermodynamics
Question 2.
State the theorem of parallel axes on moment of inertia.
Answer:
The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
Question 3.
Select a TRUE statement from the following
a) Year and light year have the same dimensions.
b) Intensity of gravitational field has same dimensions as that of acceleration.
c) One angstrom is the mean distance between sun and earth.
d) Parsec is a unit of time.
Answer:
b) Intensity of gravitational field has same dimensions as that of acceleration.
Question 4.
If the zero of potential energy is at infinity, the total energy of an orbiting satellite is negative of its ……… energy.
Answer:
Kinetic energy
Question 5.
What is the time period of a second’s pendulum?
Answer:
2s
Answer any five questions from question numbers 6 to 11. Each carry two scores. (5 × 2 = 10)
Question 6.
Using a suitable velocity time graph derive the relation x = \(v_{0} t+\frac{1}{2} a t^{2}\)
Answer:
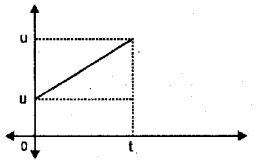
Consider a body moving with an acceleration ‘a’. Let ‘u’ be the initial velocity at t = 0 and final velocity ‘v’ at t = t.
The area of velocity- time graph gives displacement.
ie. Area = Area of rectangle + Area of triangle.
= ut + \(\frac{1}{2}\)(v – u)t ………(1)
But we know a = \(\frac{v-u}{t}\)
(v – u) = at ………(2)
Substitute eq (2) in eq (1) we get
Area = ut + \(\frac{1}{2}\)at.t
Area = ut + \(\frac{1}{2}\)at2
Area gives displacement
∴ displacement, S = ut + \(\frac{1}{2}\)at2
Question 7.
A boy throws a ball of mass 200g with a velocity 20 ms-1 at an angle of 40° with the horizontal. What is the kinetic energy of the ball at the highest point of the trajectory?
Answer:
Kinetic energy of ball at the highest point of trajectory = \(\frac{1}{2}\)mu2cos2θ
m = 200g
θ = 40°
u = 20 ms-1
KE = \(\frac{1}{2}\) × 0.2 × (20 × cos40)2
= 23.47J
Question 8.
Write the work done in each of the following cases as zero, positive or negative.
a) Work done by centripetal force in circular motion.
b) Work done by friction.
c) Work done by gravitational force on a freely falling object.
d) Work done by the applied force in lifting an object.
Answer:
a) Zero
b) Negative
c) Positive
d) Positive
Question 9.
Derive an expression for the escape velocity of an object from the surface of a planet.
Answer:
Force on a mass m at a distance r from the centre of earth = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\)
Work done for giving small displacement dr,
dw = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}} \mathrm{dr}\)
Work done in taking the body to infinity from surface of earth,

Question 10.
A typical stress-strain graph of a metallic wire is shown below.
a) Write the name of the point B labelled in the graph.
b) For the materials like copper the points D and E are ……(close/far apart)
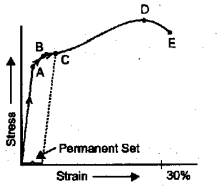
Answer:
a) Yield point or elastic limit
b) Far apart
Question 11.
The terminal velocity of a copper ball of radius 2mm falling through a tank of oil at 20°C is 6.5 cms-1. Calculate the viscosity of the oil at 20°C.
(Hints: Density of oil is 1.5 × 103 kgm-3, density of copper is 8.9 × 103kgm-3)
Answer:
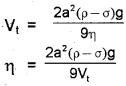

Answer any five questions from question numbers 12 to 17. Each carry two scores. (5 × 2 = 10)
Question 12.
A body falling under the effect of gravity is said to be in free fall.
a) Draw the velocity-time graph for a freely falling object.
b) Define uniform acceleration.
c) From the given figures which represents uniformly accelerated motion.
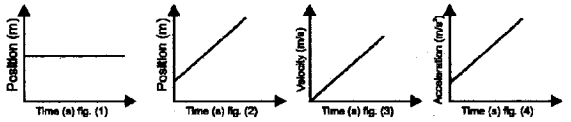
Answer:
a)
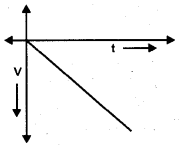
b) A body is said to be in uniform acceleration if velocity changes equally in equal intervals of time. It means acceleration is constant. eg. free fall
c) Figure 3
Question 13.
A gun moves backward when a short is fired from it.
a) Choose the correct statement
i) The momentum of the gun is greater than that of the shot.
ii) The momentum acquired by the gun and shot have the same magnitude.
iii) Gun and shot acquire the same amount of kinetic enegry.
b) A shell of mass 0.020 kg is fired by a gun of mass 100 kg. If the muzzle speed of the shell is 80m/s, what is the recoil speed of the gun?
Answer:
a) ii) The momentum acquired by the gun and shot have the same magnitude.
b) V = \(\frac{\mathrm{mv}}{\mathrm{M}}\)
mass of gun M = 100 kg
mass of shell, m = 0.02 kg
v = 80 m/s
V = \(\frac{0.02 \times 80}{100}\) = 0.016 m/s
Question 14.
Acceleration due to gravity decreases with depth
a) Prove the above statement by deriving proper equation.
b) Using the equation, show that acceleration due to gravity is maximum at the surface and zero at the center of the earth.
Answer:
a) If we assume the earth as a sphere of radius R with uniform density r,
mass of earth = volume × density

Question 15.
A device used to lift automobiles is shown in the figure.
a) Write the name of the device.
b) In the situation shown in the figure, mass of the car is 3000 kg and are of the piston carrying it is 425 cm2. What pressure is to be applied to the smaller piston?
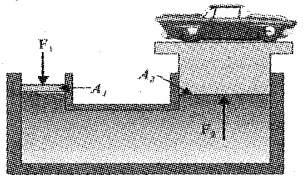
Answer:
a) Hydraulic lift
b) Area A = 425 cm2 = 425 × 10-4 m2
m = 3000 kg
F = mg
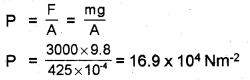
Question 16.
Based on the kinetic theory of gases, derive an expression for the pressure exerted by an ideal gas.
Answer:
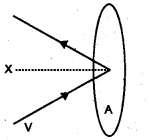
Consider molecules of gas in a container. The molecules are moving in random directions with a velocity V. This is the velocity of a molecule in any direction. The velocity V can be resolved along x, y and z directions as Vx, Vy, and Vz respectively. If we assume a molecule hits the area A of container with velocity Vx and rebounds back with -Vx. (The velocities Vx and Vy do not change because this collision is perfectly an elastic one).
Therefore, the change in momentum imparted to the area A by the molecule = mvx – -mVx
= 2mVx
To find the total number of collisions taking place in a time t, consider the motion of the molecules towards the wall. The molecules covers a distance Vxt along the x direction in a time t. All the molecules within the volume AVxt will collide with the area in a timet.
If ‘n’ is the number of molecules per unit volume, the total number of molecules hitting the area A,
N = AVxt n
But on an average, only half of those molecules will be hitting the area, and the remaining molecules will be moving away from the area. Hence the momentum imported to the area in a time t
Q = 2mvx × \(\frac{1}{2}\)AVxtn
= nmVx2At
The rate of change of momentum,
\(\frac{Q}{t}\)
But rate of change of momentum is called force, ie. force F = nmVx2A
∴ pressure P = nmVx2A
Different molecules move with different velocities. Therefore, the average value V2x is to betaken. If \(\overline{\mathrm{v}}_{\mathrm{x}}^{2}\)
V2x is the average value then the pressure.
p = \(\overline{\mathrm{v}}_{\mathrm{x}}^{2}\) ………..(1)
\(\overline{\mathrm{v}}_{\mathrm{x}}^{2}\) is known as the mean square velocity.
Since the gas is isotropic (having the same properties in all directions), we can write
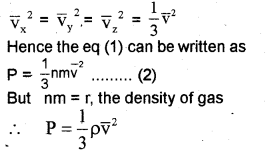
Question 17.
When 0.15 kg of ice at 0°C is mixed with 0.30 kg of water at 50°C in a container, the resulting temperature is 6.7° C. Calculate the latent heat of fusion of ice. Given specific heat capacity of water 4186 Jkg-1K-1.
Answer:
Heat lost by water = heat gained by ice
0.15 × L + 0.15 × 4186 × 6.7 = 0.30 × 4186 × (50 – 6.7)
0.15L = 0.30 × 4186 × 43.3 – 0.15 × 4186 × 6.7
= 50169.21
L = \(\frac{50169.21}{0.15}\) = 336.46 KJ
Answer any four questions from question numbers 18 to 22. Each carries four scores. (4 × 4 = 16)
Question 18.
The accuracy in measurement depends on the limit or the resolution of the measuring instrument.
a) State whether the above statement is TRUE or FALSE.
b) A physical quantity P is related to four observables a, b, c and d as P = \(\frac{a^{3} b^{2}}{\sqrt{c d}}\). The percentage errors in measurements of a, b, c and d are 1%, 3%, 2% and 3% respectively. What is the percentage errors in the measurement of P?
Answer:
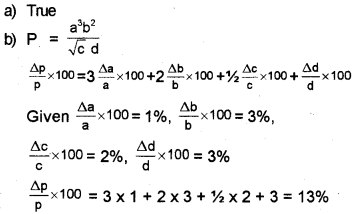
Question 19.
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed.
a) What is the angle between velocity and acceleration at any instant of motion?
b) If the stone makes 14 revolutions in 25s, what is the magnitude of acceleration of the stone?
Answer:
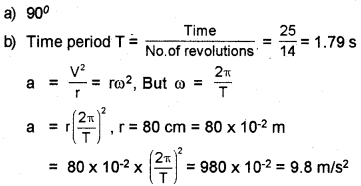
Question 20.
a) If \(\overline{\mathrm{A}}\) is perpendicular to \(\overline{\mathrm{B}}\), what is the value of \(\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}\)?
b) Find the angle between the force
\(\overline{\mathrm{F}}=(3 \hat{i}+4 \hat{j}-5 \hat{\mathrm{k}}) \mathrm{N}\) and displacement
\(\overline{\mathrm{d}}=(5 \hat{i}+4 \hat{j}+3 \hat{k}) \mathrm{m}\)
Answer:

Question 21.
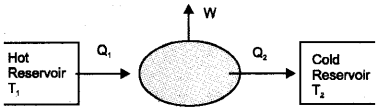
Schematic diagram of a device is given below.
a) Write the equation for the erfficency of the device?
b) Write the name of the four process in the working cycle of the device.
c) If T1 = 100°C, T2 = 0°C and Q1 = 4200J, find the value of Q2.
Answer:
a) η = 1 – \(\frac{Q_{2}}{Q_{1}}\) or η = 1 – \(\frac{T_{2}}{T_{1}}\)
b) Isothermal expansion, adiabatic expansion, isothermal compression and adiabatic compression.
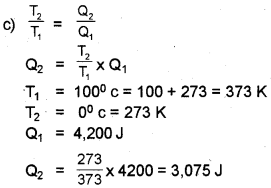
Question 22.
a) Which one of the following relationships between the acceleration (a) and the displacement (x) of a particle involve simple harmonic motion?
i) a = 0.7x
ii) a = -200x2
iii) a = -10x
iv) a = 100x3
b) A simple harmonic motion is represented as x = A cosωt. Obtain the expression for velocity and acceleration of the object and hence prove that acceleration is directly proportional to the displacement.
Answer:
a) iii) a = -10x
b) The y displacement of S.H.M. is given by
y = asinωt
∴ velocity in y direction

Answer any three questions from question numbers 23 to 26. Each carries five scores. (3 × 5 = 20)
Question 23.
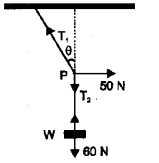
a) What is the condition for the equilibrium of concurrent forces?
b) A mass of 6 kg is supended by a rope of length 2 m from the ceiling. A force of 50 N in the horizontal direction is applied at the midpoint P of the rope a shown. What is the angle, the rope makes with the vertical in equilibrium (Take g = 10ms-2)
Neglect the mass of the rope.
c) What will be the angle made by the rope with the vertical if its length is doubled?
Answer:
a) Vector sum of all forces should be zero.
b) T1 sinθ = 50 N ……(1)
T2 sinθ = 60 N
dividing (1) by (2)
we get tanθ = \(\frac{5}{6}\)
θ = tan-1 (\(\frac{5}{6}\)) = 40°
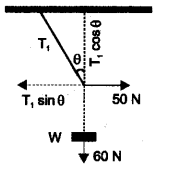
c) No change in angle
Question 24.
a) Write the equation connecting torque with force.
b) A meter stick is balanced at its centre (50 cm).
When two coins each of mass 5 g are put on the top of the other at the 12 cm mark, it is found to be balanced at 45 cm. What is the mass of the stick?
c) Derive the relation connecting torque with angular momentum.
Answer:
a) \(\vec{\tau}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{f}}\), τ = rf sinθ
b)
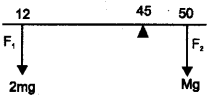
Mass of coin m = 5 gm
Force F1 = 2 × 5g
Force F2 = Mg
According to the principle of moment 2 × 5g × 33 = 5 × Mg
∴ M = 66 gm
c) Angular momentum of a particle, \(\vec{l}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}\)
When differentiate on both side, we get
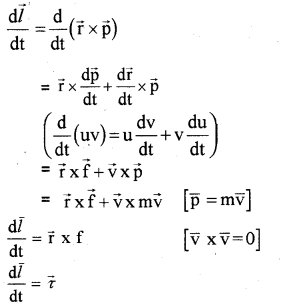
Question 25.
a) Water rises up in a narrow tube inspite of gravity. This phenomenon is called…….
b) Derive an expression for the height of water in the tube in terms of radius of the tube and surface tension of the liquid.
c) Water with detergent dissolved in it should have …. angle of contact, (small/large)
Answer:
a) Capillary rise
b) Expression for capillary rise
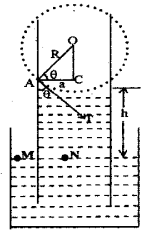
Consider a capillary tube of radius ‘a’ dipped in a liquid of density r and surface tension S. If the liquid has a concave meniscus it will rise in the capillary tube. Let h be the rise of the liquid in the tube. Let p1 be the pressure on the concave side of the meniscus and po, that on the other side.
The excess pressure on the concave side of the meniscus can be written as
Pi – Po = \(\frac{2 \mathrm{~S}}{\mathrm{R}}\) ……..(1)
Where R is the radius of the concave meniscus.
The tangent to the meniscus at the point A makes an angle q with the wall of the tube.
In the right angled triangle ACO
cosθ = \(\frac{a}{R}\)
∴ R = \(\frac{\mathrm{a}}{\cos \theta}\)
substituting the values of R in the equation (1)
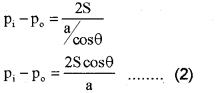
Considering two points M and N in the same horizontal level of a liquid at rest, pressure at N = pressure at M
But pressure at M = pi, the pressure over the concave meniscus and pressure at N = po + hng
∴ Pi = Po + hrg
or pi – po = hrg …….(3)
From equations (2) and (3), we get
hρg = \(\frac{2 \mathrm{~S} \cos \theta}{\mathrm{a}}\)
h = \(\frac{2 \mathrm{~S} \cos \theta}{\mathrm{a} \rho \mathrm{g}}\)
Question 26.
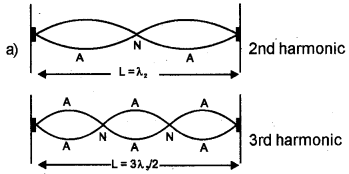
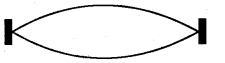
The fundamental mode of vibration of a stretched string is shown below.
a) Draw the second and third harmonies.
b) Prove that frequencies produced in the string are in the ratio 1 : 2 : 3
c) Let the fundamental frequency is 45 Hz and the length of the wire is 87.5 cm. If linear density of the wire is 4.0 × 10-2 kg/m. Find the tension in the string.
Answer: