Kerala Plus One Physics Previous Year Question Paper March 2019 with Answers
| Board | SCERT |
| Class | Plus One |
| Subject | Physics |
| Category | Plus One Previous Year Question Papers |
Time: 2 Hours
Cool off time: 15 Minutes
Maximum: 60 Scores
General Instructions to candidates:
- There is a ‘cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read the instructions carefully.
- Read questions carefully before you answering.
- Calculations, figures, and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non-programmable calculators are not allowed in the Examination Hall.
Answer any three questions from 1 to 4. Each carry one score. (3 × 1 = 3)
Question 1.
“The weak nuclear force is stronger than gravitational force.” State whether this statement is TRUE or FALSE.
Answer:
True
Question 2.
Position (x) – time (t) graphs of two objects A and B are shown below. At what time the objects meet?
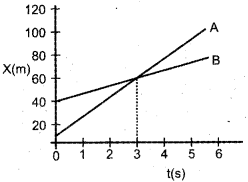
Answer:
3 Sec
Question 3.
Write any two properties of conservative force.
Answer:
- The work done by the conservative force depends only on the end points.
- The work done by conservative force in a closed path is zero
Question 4.
State first law of thermodynamics.
Answer:
According to first law of thermodynamics, heat supplied to a system is used to increase its internal energy and to do work.
Answer any six questions from 5 to 11. Each carries two scores. (6 × 2 = 12)
Question 5.
Draw a graph showing the variation of volume of a given mass of water with temperature from 0°C. In the graph mark the temperature at which water has maximum density.
Answer:
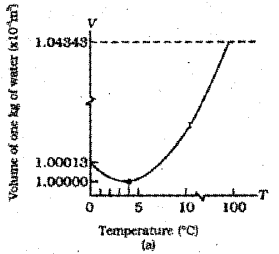
Question 6.
What is sublimation? Write an example for a sublime material.
Answer:
Transition of solid into gas without forming liquid is called sublimation.
Example: Camphor
Question 7.
The lengths of two bodies measured by a metre scale are
I1 = (20 ± 0.5) cm and
I2 = (15 ± 0.2) cm.
Calculate:
a) Sum of these lengths.
b) Difference between the lengths.
Answer:
i) l1 = 20, Δl1 = 05, l2= 15, Δl2 = 02
Sum of length l = l1 + l2
= 20 + 15 =35
error Δl = Δl1 + Δl2
= 0.5 + 0.2 = 0.7
∴ Sum = 35+ 0.7
ii) Difference = l1 – l2
= 20 – 15 = 5
error = Δl1 + Δl2
= 0.5 + 0.2 = 0.7
∴ Difference = 5 + 0.7 = 5 ± 0.7
Question 8.
Match the following.
| A | B | ||
| a) | Torque (\( \bar{\tau}\)) | i) | Perpendicular to \(\bar{r}\) and \(\bar{P}\) |
| b) | Angular Momentum (\(\bar{L}\)) | ii) | Σ(\(\bar{F}\)) |
| c) | Rotational equilibrium | iii) | \(\bar{\omega} \times \bar{r}\) |
| d) | Linear velocity \(\bar{v}\) | iv) | \(\bar{r} \times \bar{F}\) |
| v) | Σ\( \bar{\tau}\) | ||
Answer:
Torque – \(\bar{r} \times \bar{F}\)
Angular momentum – Perpendicular to \(\bar{r}\) and \(\bar{P}\)
Rotational equilibrium – \(\Sigma \bar{\tau}\) = 0
Linear velocity – \(\bar{\omega} \times \bar{r}\)
Question 9.
Derive an expression for escape speed from a planet.
Answer:
Escape Speed: The minimum speed with which a body is projected so that it never returns to the earth is called escape speed or escape velocity.
Expression for escape speed:
Force on a mass m at a distance r from the centre of earth = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\)
Work done for giving small displacement dr,
dw = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\)dr
Work done in taking the body to infinity from surface of earth,
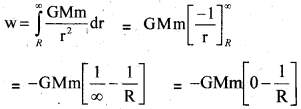
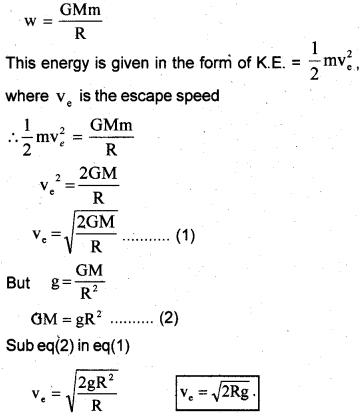
Question 10.
A wave travelling along a string is described by, y (x, t) = 0.005 Sin(80.0x – 3.0t) in which the numerical constants are in SI units. Calculate the wavelength and frequency of the wave.
Answer:
The equation for wave
y(x, t) = 0.005 Sin (80.0x – 3.01)
Compare this equation with standard wave equation.
y(x, t) = A sin (kx – wt)
We get kx = 80x
\(\frac{2 \pi}{\lambda}\) = 80
λ = 0.0785 m
ωt = 3t
ω = 3
2πf = 3
f = 0.48 Hz
Question 11.
a) Draw diagrams showing the first and third harmonics produced in a closed pipe.
b) Write the equation for the fundamental frequency in terms of length of the pipe.
Answer:
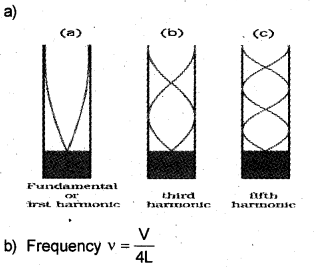
Answer any five questions from 12 to 17. Each carries three scores . (5 × 3 = 15)
Question 12.
“Velocity can not be added to temperature”.
a) This is in accordance with which law of Physics?
b) Check the dimensional correctness of the equation PV = Fx where P is the pressure, V is volume, F is force and x is displacement.
Answer:
a) Principle of homogeneity
b) PV = Fx
dimension of PV = workdone
∴ PV = ML2T-2
Dimension of Fx = ML2T-2
Hence the equation is correct.
Question 13.
Find the magnitude of the resultant of two vectors A and B in terms of their magnitudes and angle θ between them.
Answer:
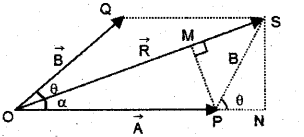
Consider two vectors \(\overrightarrow{\mathrm{A}}\) (=\(\overrightarrow{\mathrm{OP}}\)) and \(\overrightarrow{\mathrm{B}}\) (=\(\overrightarrow{\mathrm{OQ}}\)) making an angle θ.
Using the parallelogram method of vectors, the resultant vector R can be written as,
\(\overrightarrow{\mathrm{R}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\)
SN is normal to OP and PM is normal to OS. From the geometry of the figure
OS2 = ON2 + SN2
but ON = OP + PN
i.e., OS2 = (OP + PN)2 + SN2 ………..(1)
From the triangle SPN, we get
PN = Bcos θ and SN = Bsin θ
Substituting these values in eq.(1), we get
OS2 = (OP + Bcos q)2 + (Bsin q)2
But OS = R and OP = A
R2 = (A + Bcosθ)2 + B2sin2θ
= A2 + 2AB cosθ + B2cos2θ + B2sin2θ
R2 = A2 + 2AB cosθ + B2
R = \(\sqrt{\mathrm{A}^{2}+2 \mathrm{AB} \cos \theta+\mathrm{B}^{2}}\)
The resultant vector \(\overrightarrow{\mathrm{R}}\) make an angle a with \(\overrightarrow{\mathrm{A}}\).
From the right angled triangle OSN,
tan α = \(\frac{\mathrm{SN}}{\mathrm{ON}}=\frac{\mathrm{SN}}{\mathrm{OP}+\mathrm{PN}}\)
But SN = Bsinθ and PN = Bcosθ
∴ tan α = \(\frac{B \sin \theta}{A+B \cos \theta}\)
Question 14.
a) Figure shows the path of an object in uniform circular motion.
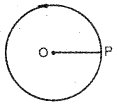
Redraw the figure and mark the directions of velocity and acceleration of the particle at P.
b) An object moving uniformly in a circular path of radius 12 cm completes 7 revolutions in 100s. What is the angular speed, and the linear speed of the motion?
Answer:
a)
Radius r = 12 × 10-2m
7 rotations = 100 sec
∴ frequency, f = \(\frac{7}{100}\) Hz
or ω = 2πf
= 2π × \(\frac{7}{100}\)
= 0.44 rad/s
linear velocity v = rω
v = 12 × 10-2 × 0.44
= 0.053 m/s
Question 15.
A light bullet is fired from a heavy gun.
a) Choose the CORRECT.
i) Speed of the gun and the bullet are equal.
ii) Momenta of the bullet and gun are equal in magnitude and opposite in direction.
iii) Momenta of the gun and bullet are equal in magnitude and are in the same direction.
iv) Velocity of gun and bullet are equal.
b) By using a suitable conservation law in Physics, prove your above answer.
Answer:
a) (ii)
b) Consider a gun of mass M and bullet m. When gun fires, the fun moves with velocity V and bullet moves with velocity u. According to conservation of momentum.
Total momentum before firing = Total momentum after firing.
∴ O + 0 = MV + mv
MV = -mv
Question 16.
BY using the law of equipartition of energy, derive the value of ratio of specific heats of a monoatomic gas.
Answer:
The energy of a single monoatomic gas = 3 × \(\frac{1}{2}\)KBT.
The energy of one mole monoatomic gas = 3 × \(\frac{1}{2}\)KBT × NA
[one mole atom contain Avogadro number (NA) of atoms]

Question 17.
a) Figure shows the strain-stress curve for a material.
What is the Young’s modulus of the material?
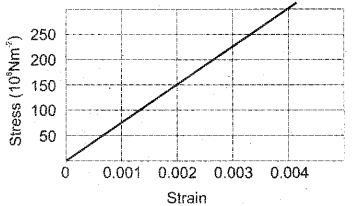
b) Young’s modulus of Aluminium is 70 × 109 Nm-2 and that of copper is 120 × 109Nm-2. Same strain is to be produced on an aluminium wire and a copper wire of equal cross section. Which wire requires more force?
Answer:
a) Slope of the graph gives, Youngs modulus

Copper has more Youngs modules than aluminium wire.
Answer any five questions from 18 to 23. Each carries four scores. (5 × 4 = 20)
Question 18.
Free fall is a uniformly accelerated motion.
a) Draw the velocity time graph of free fall.
b) A ball is thrown vertically upwards with a velocity of 20 ms-1 from the top of a building. The height of the point from where the ball is thrown is 25.0 m from the ground.
i) How high will the ball rise?
ii) How long will it be before the ball hits the ground?
Answer:
b) i) u = 20 m/s, v =0,
∴ v2 = u2 + 2as
O = (20)2 + -2 × 10 × s
20s = 202
S = 20 m
ii) u = 20, s = -25m, a =-10 m/s2
s = ut + \(\frac{1}{2}\)at2
-25 = 20 × t – \(\frac{1}{2}\) × 10 × t2
-25 = 20t – 5t2
5t2 – 20t – 25 = 0
t2 – 4t – 5 =0
Solving this, we get t = 5 sec
Question 19.
Power is the rate at which work is done.
a) Express power in terms of force and velocity.
b) An elevator carrying the maximum load of 1800 kg is moving up with a constant speed of 2ms-1.
The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator.
c) Express your above answer in horse power.
Answer:
a) P = FV
b) Total force F = mg + Ffriction
F = 1800 × 10 + 4000
F = 22000 N
∴ Power P = Fv
= 2200 × 2 = 44000 W
c) 1 Hp = 746 wait
∴ power in Hp = \(\frac{44000}{746}\) = 58.98 Hp
Question 20.
Starting from rest, a solid sphere rolls down an inclined plane of vertical height h without slipping.
a) If M is the mass and R is the radius of the sphere, write an equation for the moment of inertia of the above sphere about a diameter.
b) Prove that the velocity with which the sphere reaches the bottom of the plane is 1.2\(\sqrt{\mathrm{gh}}\)
c) If instead of sphere another object of the same mass and radius with a different shape is used in the above experiment, will it reach the bottom with the same or different velocity?
Answer:
a) I = \(\frac{2}{5}\)MR2
b) Potential energy is converted into translational kinetic energy and rotational kinetic energy.

c) Different velocity
Question 21.
Earth satellites are objects which revolve around the earth.
a) Time period of a geostationary satellite is…….
b) Derive an expression for the time period of a satellite.
c) By using the expression you derived above, show that motion of satellite obeys Kepler’s law of periods.
Answer:
a) 24 hrs
b) Consider a satellite of mass m revolving with orbital velocity V around the earth at a height ‘h’ from the surface of earth. Let M be the mass of earth and R be radius of earth.
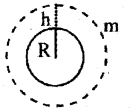
The gravitational force of attraction between earth and satillite
F = \(\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})^{2}}\)
Centripetal force required for the satellite
F = \(\frac{\mathrm{mv}^{2}}{(\mathrm{R}+\mathrm{h})}\)
For stable rotation,
Centripetal force = Gravitational force

c) T2 ∝ r3
Question 22.
a) Define angle of contact.
b) Water proofing agents are added to create a …… (large/small) angle of contact between the water and fibres.
c) Calculate the excess of pressure inside an air bubble of radius 1 mm formed just below the free surface of water. Given surface tension of water 72 × 103 Nm-1.
Answer:
a) Angle of contact is the angle between the solid surface and the tangent drawn to the liquid surface at the point of contact inside the liquid.
b) Large
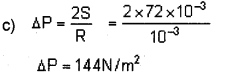
Question 23.
Schematic diagram of a heat engine is shown below.
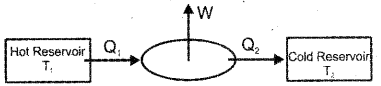
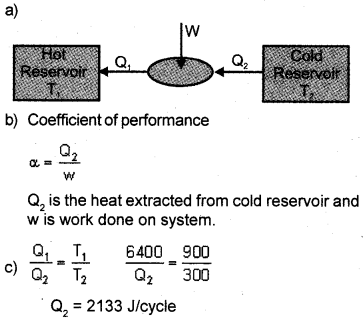
a) Modify the given diagram for a refrigerator.
b) Write the equation for the coefficient of performance of a refrigerator.
c) In the given diagram, T1 = 900K, T2 = 300K, Qr = 6400J/cycle
calculate the value of Q2
Answer:
Answer any two questions from 24 to 26. Each carries five scores. (2 × 5 = 10)
Question 24.
Static friction opposes impending motion.
a) Write the mathematical equation connecting the limiting value of static friction with normal reaction.
b) Choose the CORRECT statement:
i) Both kinetic friction and static friction are independent of the area of contact.
ii) Kinetic friction depends on area of contact but static friction do not.
iii) Static friction depends on area of contact but kinetic friction do not.
iv) Both kinetic friction, and static friction depend on the area of contact.
c) A mass rests on a horizontal plane. The plane is gradually inclined until at an angle θ with the horizontal, the mass just begins to slide. Show that the coefficient of static friction between the block and the Surface is equal to Tan θ.
Answer:
a) fs max = µsN
b) (i)
c) Consider a body placed on a inclined plane. Gradually increase the angle of inclination till the body placed on its surface just begins to slide down. If α is the inclination at which the body just begins to slide down, then α is called angle of repose.

The limiting friction F acts in upward direction along the inclined plane. When the body just begins to move, we can write
F = mg sin α ……(1)
from the figure normal reaction,
N = mg cos α ……(2)
dividing eq (1) by eq (2)
\(\frac{\mathrm{F}}{\mathrm{N}}=\frac{\mathrm{mg} \sin \alpha}{\mathrm{mg} \cos \alpha}\)
µ = tan α …….(3)
Question 25.
a) Derive Bernoulli’s equation for the stream line flow of an incompressible liquid.
b) Figures (a) and (b) refer to the steady flow of a (nonviscous) liquid. Which of the following two figures is INCORRECT?
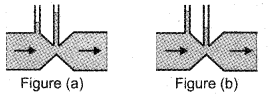
Answer:
a)
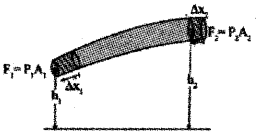
Consider an incompressible liquid flowing through a tube of non uniform cross section from region 1 to region 2. Let P1 be the pressure, A1 the area of cross section and V1 the speed of flow at the region 1. The corresponding values at region 2 are P2, A2 and V2 respectively. Region 1 is at a height h1 and region 2 is at a height h2.
The workdone on the liquid in a time Δt at the region 1 is given by
W1 = force × distance
= P1A1Δx1 = P1ΔV1
(∵ A1Δx1 = ΔV)
Where Δx1 is the displacement produced at region 1, during the time interval Δt.
Similarly the workdone in a time Δt at the region 2 is given by,
W2 = -P2 A2 ΔY2 = -P2 ΔV2
[Here -ve sign appears as the direction of p and Ax are in opposite directions.]
Net workdone. DW= P1ΔV1 – P2ΔV2
According the equation of continuity
ΔV1 = ΔV2 = ΔV
∴ ΔW = P1ΔV – P2ΔV
ΔW = (P1 – P2)ΔV …….(1)
This work done changes the kinetic energy, pressure energy and potential energy of the fluid.
If Δm is the mass of liquid passing through the pipe in a time Δt, the change in Kinetic energy is given by
Δk.E = \(\frac{1}{2} \Delta \mathrm{mV}_{2}^{2}-\frac{1}{2} \Delta \mathrm{mV}_{1}^{2}\)
Δk.E = \(\frac{1}{2}\)Δm(\(\mathrm{V}_{2}^{2}\) – \(\mathrm{V}_{1}^{2}\)) ……..(2)
Change in gravitational potential energy is given by
Δp.E= Amgh2 – Δmgh1
Δp.E= Δmg(h2 – h1) …….(3)
According to work-energy theorem work done is equal to the change in kinetic energy plus the change in potential energy.
ie; Δw = ΔkE + ΔPE …….(4)
Substituting eq. 1, 2 and 3 in eq. 4, we get
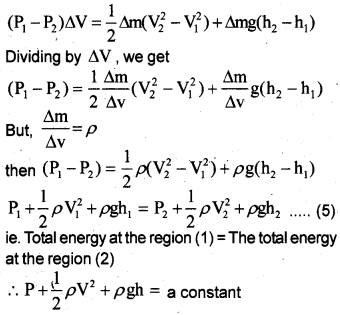
b) figure (a)
Question 26.
a) Prove that the oscillations of a simple pendulum are simple harmonic and hence derive an expression for the time period of a simple pendulum.
b) What is the length of a simple pendulum, which ticks seconds?
Answer:
a)
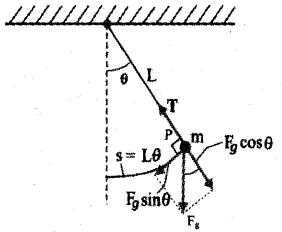
Consider a mass m suspended from one end of a string of length L fixed at the other end as shown in figure. Suppose P is the instantaneous position of the pendulum. At this instant its string makes an angle θ with the vertical.
The forces acting on the bob are (1) weight of bob Fg (mg) acting vertically downward. (2) Tension T in the string.
The gravitational force Fg can be divided into a radial component FgCosθ and tangential component FgSinθ. The radial component is cancelled by the tension T. But the tangential component FgSinθ produces a restoring torque.
Restoring torque r = – Fgsinθ.L
τ = -mgsinθ.L …….(1)
-ve sign shown that the torque and angular displacement θ are oppositely directed. For rotational motion of bob,
τ = Iα …….(2)
Where I is moment of inertia about the point of suspension and a is angular acceleration. From eq (1) and eq (2).
Iα = -mgsinθ.L
If we assume that the displacement θ is small, sinθ ≈ θ
Iα = – mgθ.L
Iα + mgθL = 0
