Plus One Physics Notes Chapter 9 Mechanical Properties of Solids

Kerala Plus One Physics Notes Chapter 9 Mechanical Properties of Solids

Summary
Introduction
Elasticity:
The property of a material by virtue of which it regains its original shape on the removal of the deforming force is called elasticity. The deformation caused is known as elastic deformation.

Plasticity:
The property of a material by virtue of which it does not regain its original shape on the removal of the deforming force is called plasticity. The substance which shows this property is called plastic.

Elastic Behavior Of Solids
In a solid, each atoms (or molecule) is surrounded by neighboring atoms (or molecules). These atoms are bonded by inter atomic forces. When a solid is deformed, the atoms are displaced from their equilibrium positions. When the deforming force is removed, the interatomic force bring back atoms into its original position. Thus body regains its original shape and size.

Stress And Strain Stress
It is the restoring force developed per unit area of cross section

S.I unit of stress is Nm² or Pascal (Pa) and its dimensional formula is [ML^-1 T^-2]. The restoring force is equal and opposite to the external applied force.
Strain:
The effect of stress on a body is called strain. Strain is measured as the ratio of the change in dimension produced to the original dimension.

Different types of Stress and Strain:
There are three ways in which a solid may change its dimensions when an external force acts on it. Hence there are three types of stress and corresponding strain.

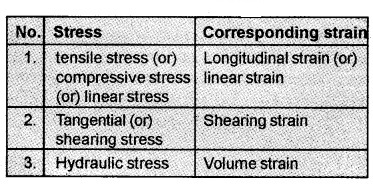
1. Tensile Stress and Longitudinal Strain:
When the forces acting on the body produces an elongation along its length, then we call the stress as tensile stress (see figure).

When the forces acting on the body produces a compression along its length, then we call the stress as compressive stress. The tensile stress produces a change in the length (∆L). Hence the longitudinal strain can be written as
Longitudinal strain = \(\frac{\text { Change in length }}{\text { Original length }}\)
Longitudinal strain = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}\)
Where ‘L’ is the original length.

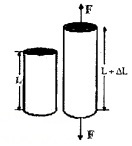
2. Tangential (or) Shearing Stress and Shearing Strain:

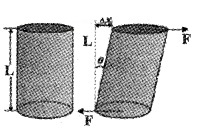
If two equal and opposite deforming forces are applied parallel to cross-sectional area of the cylinder as shown in figure, there is a relative displacement between the opposite faces of the cylinder. The restoring force per unit area developed due to the applied tangential force is known as tangential or shearing stress.

As a result of applied tangential force, there is a relative displacement between opposite faces of the cylinder (see figure). The strain so produced is known a shearing strain. Shearing strain can be written as,

Where θ is the angular displacement of the cylinder from the vertical (original position of the cylinder). Since θ is very small, tanθ ≈ θ.

3. Hydraulic Stress and Volume Strain:

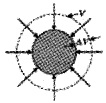
Consider a solid placed inside the fluid. The force applied by the fluid acts in perpendicular direction at each point of the surface. This leads to decrease in its volume without any change of its geometrical shape.

The internal restoring force per unit area in this case is known as hydraulic stress. The strain produced by a hydraulic pressure is called volume strain. The volume stress can be written as
Volume strain = \(\frac{\text { Change in volume }}{\text { Original volume }}=\frac{\Delta \mathrm{V}}{\mathrm{V}}\)
Note: Hydraulic Stress is equal to the hydraulic pressure.

Hooke’S Law
Hooke’s law:
For small deformations, the stress and strain are proportional to each other, ie: stress ∝ strain. Stress = k × strain Where k is the proportionality constant and is known as modulus of elasticity.

Stress Strain Curve

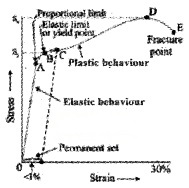
A typical graph for stress – strain graph for a metal is given in the figure.
Region OA:
In the region between O to A, the curve is linear. Hence in this region Hooke’s law is obeyed. The body regains its original dimensions when the applied force is removed. In this region the material behaves as an elastic body.

Region AB:
In this region stress and strain are not proportional. The material returns to its original dimension when the applied force (stress) is removed. The point B in the curve is known as yield point (also known as elastic limit) and corresponding stress is yield strength of the material.

Region BD:
If the applied force exceeds the yield strength, strain increases rapidly for a small change in the stress. When the applied force (stress) is removed at ‘C’, the body does not regain it’s original dimension, (even when the stress is zero, the strain is not zero).

This deformation is said to be plastic deformation and the material is said to have a permanent set. The point D on the graph is the ultimate tensile strength of the material.

Region DE:
Beyond this point D, additional strain is produced even by a reduced applied force and fracture occurs at point E. Point E is called a fracture point. If the ultimate strength (D) and fracture point (E) are close, the material is said to be brittle. If they are far apart, the material is said to be ductile.

Elastomers:
For rubber-like materials, even for small stress, the strain produced will be very high. Such materials are called elastomers.

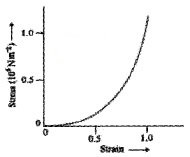
There is no plastic flow region in the curves for elastomer materials. The elastic tissues of our blood vessel (aorta) is another example for elastomer.
Note: elastomer materials do not obey Hooke’s law.

Elastic Moduli
According to Hooke’s law

where k is called modulus of elasticity.
Depending on different types of stress and strain, there are 3 types of modulus of elasticity.
Different types of modulus of elasticity

1. Young’s modulus (Y)
2. Shear modulus (G)
3. Bulk modulus (B)

1. Youngs Modulus:
Young’s modulus is defined as the ratio of tensile stress (α) to the longitudinal strain (ε).
ie; Youngs modulus Y = \(\frac{\text { tensile stress }}{\text { longitudinal strain }}\)
Y = \(\frac{\alpha}{\varepsilon}\)
Explanation:
Consider a wire of length L and area of cross section a, fixed at one end and loaded at the free end with a weight mg. Let l be the elongation. Then tensile strain α = \(\frac{F}{a}\)
Longitudinal strain ε = \(\frac{l}{L}\)

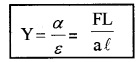
2. Determination of youngs modulus of the material of a wire:
Experimental setup:

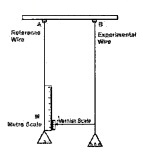
An experimental arrangement to determine the young’s modulus of a wire is shown in the figure. It consists of two long straight wires A and B. (The wire Ais called reference wire and B is called experimental wire).

A millimeter scale (main scale) is fixed near to the wire A. At bottom of wire A there is a pan to place a weight. The wire B also carries a pan in which known weights can be placed. At bottom of wire B, there is a pointer. A vernier scale is attached to this pointer. This vernier scale of B and main scale of A are placed very close to each other.

Determination of Young’s modulus:
Keep the wires (A and B) as straight by placing sufficient load at pans and note down initial reading. Then the experimental wire (B) is loaded with more weights. Note down the reading again. The difference between initial reading and final reading gives the elongation.

Let rand L be the initial radius and length of the experimental wire, then the area of cross-section of the wire is πr². Let µ be the mass that
produced an elongation ∆L in the wire.

3. Shear Modulus:

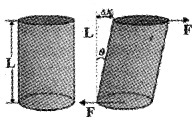
The ratio of shearing stress to the corresponding shearing strain is called the shear modulus of the material (represented by G). It is also called the modulus of rigidity.

But from figure tanθ = \(\frac{\Delta x}{L}\) = tanθ ≈ θ
∴ G = \(\frac{F}{A \theta}\) The shearing stress α_s can also be expressed as α_s = Gθ.

4. Bulk modulus (B):
When a body is immersed in a fluid, it undergoes hydraulic stress (equal in magnitude to the hydraulic pressure.) This leads to a decrease in the volume of the body. This decrease in volume produces a strain is called volume strain.

The ratio of hydraulic stress to the corresponding hydraulic strain is called the bulk modulus. It is denoted by symbol B. ie; Bulk modulus

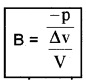
The minus sign indicates the fact that with an increase in pressure, a decrease in volume occurs. S.l. unit of the bulk modulus is the same as that of pressure ie; Nm^-2 (or) Pa.
Compressibility (k):
The reciprocal of the bulk modulus is called
compressibility, k = \(\frac{1}{B}\)
Note: Bulk modulus of solids > Bulk modulus of liquid > Bulk modulus of gases.

Question 1.
Solids are least compressible but gases are most compressible. Why?
Answer:
The molecules in solids are strongly coupled with neighboring atoms. But molecules in gases are very poorly coupled to their neighbors.

5. Poisson’S Ratio
When a wire is subjected to an extension along its length there will be contraction perpendicular to the length. The strain perpendicular to the applied force is called lateral strain. The strain parallel to the applied force is called longitudinal strain.

Within the elastic limit, lateral strain is directly proportional to the longitudinal strain. The ratio of the lateral strain to the longitudinal strain is called Poisson’s ratio.

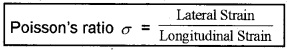
If the original diameter of the wire is d and the contraction of the wire under stress is Dd, lateral strain = \(\frac{\Delta \mathrm{d}}{\mathrm{d}}\)
If the original length of the wire is L and the elongation under stress is DL, then

Poisson’s ratio is a ratio of two strains. Hence it is a pure number and has no units or dimensions.
For steel the value is between 0.28 and 0.30.

6. Elastic potential energy in a stretched wire:
When a wire is stretched, work is done against the intermolecular forces. This work is stored in the wire as elastic potential energy.

Consider a wire of length L and area of cross-section stretched by a force F. Let l be the elongation. Then stretching force increases uniformly from 0 to F. Therefore the average force

Displacement of free end = l
∴ Workdone in stretching = F_av × l
= \(\frac{1}{2}\)Fl = \(\frac{1}{2}\) × Force × extension
This work is stored as the elastic potential energy of the wire
ie. U = \(\frac{1}{2}\) × Fl
Volume of wire =AL
Workdorie in stretching per unit volume, U = \(\frac{\frac{1}{2} F \ell}{A L}\)

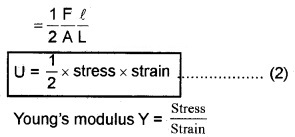
Stress = Y × strain ______(3)
Sub(3) in (2)
U = 1/2 × Y × strain × strain
U = 1/2 × Y × (strain)².

Applications Of Elastic Behavior Of Materials

1. Metallic ropes are used in the cranes for lifting the load because of its high elasticity.
2. While designing bridges and buildings, beams and columns are widely used. The bending of beams and columns under a load depends upon Young’s modulus of the material used. To reduce the bending of a beam for a given load, a material with a larger youngs modulus is to be used.
3. The maximum height of the mountain is limited by the elastic properties of the rock which holds the mountain.

Question 2.
Find the radius of the rope that used to lift 10 tons(10000Kg). Elastic limit (maximum stress) of steel is 30 × 10⁷ N/m²
Answer:
The condition to withstand a force of 100 metric ton,

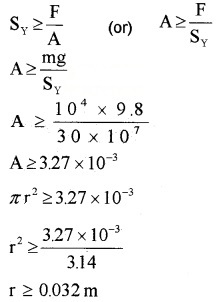
Question 3.
What is meant by buckling?

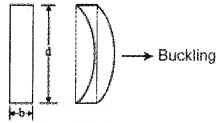
Answer:
If the load is not properly placed on a beam, the beam will bend side wise as shown in figure. This bending is called buckling.

Question 4.
Why the beams used in construction of bridges have a cross-section of the type I?
Answer:
Consider a solid rectangular beam of length l, breadth b and thickness d. If we place a load Mg at its centre, there will be a depression at the centre.

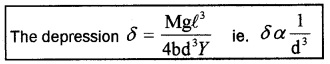
To reduce the depression at the centre, we have to increase d. But when d is large the beam will buckle unless the load is at the centre. This buckling can be avoided if the beam is given the section of the letter I. Such a beam is called I form girder.
It has following advantages

• It reduces the weight of the beam
• It saves material
• It prevents buckling

Question 5.
Find the height of mountain from the data given below. Maximum shearing stress = 30 × 10⁷ N/m² Density of material of mountain = 3 × 10³ Kgm^-3
Answer:
The force per unit area due to the weight of the mountain (at a depth h) is hrg. The material at the bottom experiences this force. The sides of the mountain are free. Hence the shear component is (hrg) itself.
∴ Shearing stress = hrg
30 × 10⁷ = h × 3 × 10³ × 10
h = 10 km
which is more than the height of Mount Everest.

Plus One Physics Notes