Plus One Physics Notes Chapter 13 Kinetic Theory

Kerala Plus One Physics Notes Chapter 13 Kinetic Theory

Summary
Introduction
The kinetic theory was developed in the nineteenth century by Maxwell, Boltzmann and other. It gives a molecular interpretation of pressure and temperature of a gas. It also explains gas laws and Avogadro’s hypothesis. It correctly explains specific heat capacities of many gases. It help us to find molecular sizes and masses.

Molecular Nature Of Matter
The scientific atomic theory is credited to John Dalton. Atomic theory is not the end of quest, but the beginning. Atoms consist of a nucleons and electrons. The nucleous itself is made up of protons and neutrons. The protons and neutrons are again made up of quarks. Even quarks may not be the end of the story.

There may be string-like elementary entities. In this chapter we shall limit ourselves to understanding the behavior of gases.

Behavior Of Gases
Gas Laws
1. Boyles law
The law states that at a given temperature, the volume of a given mass of gas varies inversely as its pressure.
It can be written as
\(P a \frac{1}{V}\) (at constant T)
PV = constant
PV = μ RT
μ → No. of moles, R → universal gas constant, T → temperature
Boyles law is not obeyed by gasses at all temperatures and pressure. Usually, Boyles, law is obeyed by gases at high temperature and low pressure (Graph is given below).

A real gas which obey this law is called ideal or perfect gas.

Variation of ‘R’ \(\left(=\frac{\mathrm{PV}}{\mathrm{T}}\right)\) with Pressure (for different temperatures)

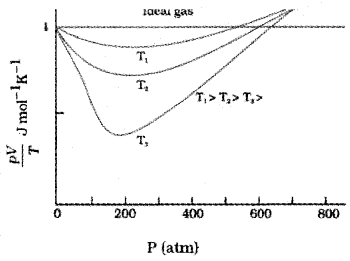
Variation of R \(\left(=\frac{\mathrm{PV}}{\mathrm{T}}\right)\) with Pressure for temperature T₁ > T₂ > T₃ is shown in the above graph. The above graph shows that, all real gases approach ideal gas behavior at low pressure and high temperature.

At low pressure or high temperature, the molecules are for apart and molecular interactions are negligible. Without interactions the gas behaves like an ideal gas.

Note:
R = 8.324 J mol^-1 k^-1.
Variation of V with P for different temperature:

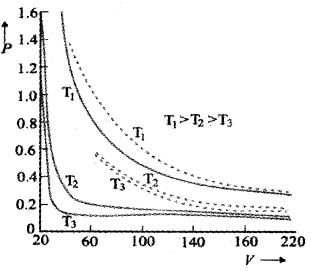
The above graph shows experimental PV curves for steam at three temperature The dotted line are the theoretical curves. (According to Boyles law). The theoretical value and experimental value comes in agreement at high temperatures and low pressures.

2. Charles law
Charles law states that the volume of a given mass of gas is proportional to its temperature when its pressure is kept constant.
V a T (P is constant)
i.e.,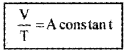

The graph between V and T:

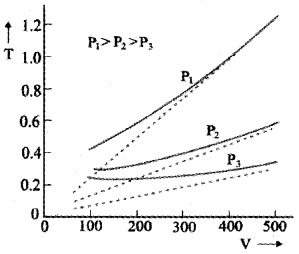
The above graph shows experimental T-V curves (solid lines) for Co₂ at three pressures compared with Charles law (dotted lines). T is in unit of 300 k and V in units of 0.13 litres.

Question 1.
Why theoretical value does not agree with experimental value?
Answer:
According to Charles law the graph between T and V is straight line. It means that when temperature decreases, the volume of gas decreases and finally becomes zero.

Practically volume will not be zero. Because the molecules require some finite space to exist. This implies that we cannot reduce its temperature to zero value. A zero kelvin temperature is only an idealized concept.

Dalton’s law of Partial Pressures:
It states that, the total pressure of a mixture of ideal gases is the sum of partial pressures.

Proof:
Consider a mixture of non-interacting ideal gases. μ₁, moles of gas 1, μ₂ moles of gas 2 etc. in a vessel of volume V at temperature T and pressure P. Using Boyles law, we can write
PV = (μ₁ + μ₂ +…………..)RT
P = \(\frac{\mu_{1} \mathrm{RT}}{\mathrm{V}}+\frac{\mu_{2} R T}{V}+\ldots \ldots \ldots\)
P = P₁ + P₂ +……………………

Kinetic Theory Of An Ideal Gas
The kinetic theory of gases has been developed by Clausius, Maxwell, Boltzmann and others. The theory is based on the following postulates.

• The gas is a collection of large number of molecules. The molecules are perfectly elastic hard spheres.
• The size of a molecule is negligible compared with the distance between the molecules.
• The molecules are always in random motion
• During their motion, the molecules collide with each other and with the walls of the containing vessel.
• The collisions are elastic and hence the total K.E energy and the total momentum of the colliding molecules before and after collisions are the same.
• The kinetic energy of a molecule is proportional to the absolute temperature of the gas.
• There is no force of attraction or repulsion between molecules.

The pressure of an ideal gas:

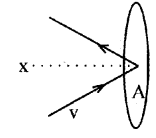
Consider molecules of gas in a container. The molecules are moving in random directions with velocity V. This is the velocity of a molecule in any direction. The velocity V can be resolved along x, y and z directions as V_x, V_y, and V_z respectively.

If we assume a molecule hits the area A of the container with velocity V_x and rebounds back with -V_x. (The velocities V_x and V_y do not change because this collision is perfectly an elastic one).

Therefore, the change in momentum imparted to the area A by the molecule
= mv_x^– – mV_x
= 2mV_x

To find the total number of collisions taking place in a time t, consider the motion of the molecules towards the wall. The molecules covers a distance V_xt along the x direction in a time t. All the molecules within the volume AV_xt will collide with the area in a time t.

If ‘n’ is the number of molecules per unit volume, the total number of molecules hitting the area A,
N = AV_xt n.

But on an average, only half of those molecules will be hitting the area, and the remaining molecules will be moving away from the area. Hence the momentum imported to the area in a time t
Q = 2mv_x × \(\frac{1}{2}\) AV_xtn.
= nmV_x²At
The rate of change of momentum,
\(\frac{Q}{t}\) = nmV_x²A
But rate of change of momentum is called force, ie. force F = nmV_x²A
∴ Pressure P = nmV_x² (P = \(\frac{F}{A}\))
Different molecules move with different velocities. Therefore, the average value V_x² is to be taken. If \(\overline{\mathbf{v}}_{\mathbf{x}}^{2}\) is the average value then the pressure.

\(p=n m \bar{v}_{x}^{2}\) ……………….. (1)

\(\overline{\mathbf{v}}_{\mathbf{x}}^{2}\) is known as the mean square velocity. Since the gas is isotropic (having the same properties in all directions), we can write

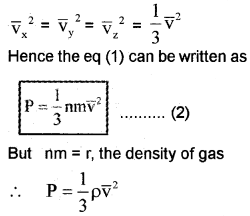
Kinetic Interpretation of gas laws:

Question 2.
Derive the ideal gas equation from P = \(\frac{1}{3} \mathrm{nm} \overline{\mathrm{v}}^{2}\)
Answer:
The average kinetic energy of the molecule is
KE = \(\frac{1}{2} m \bar{v}^{2}\) …………………….(3)
The eq (2) can be modified as

The average Kinetic energy of a molecule remains constant when the temperature is constant. That is when the temperature varies, \(\overline{\mathrm{KE}}\) also varies accordingly. The kinetic energy of a molecule is related to its absolute temperature by an equation
\(\overline{\mathrm{KE}}\) = \(\frac{3}{2}\)K_BT
Substitute equation (5) in equation (6); we get

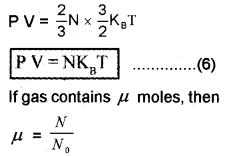
N = μ N₀
P V = μ N₀K_BT
P V = μ R T…………………… (8)
(N_BK_B = R)
This is the ideal gas equation

Deduction of Boyles law:
If the temperature is constant for gas, the eq (8) can be written as
PV = Constant
This is called Boyles law

Deduction of Charles law:
If pressure of a gas is constant, the eq (8) can be written as
V a T

This is called Charles law.

Deduction of Avogadro’s Hypothesis:
If P₁, T₁, and V constant, N₀ will be constant, ie. equal Volumes of all gases, under the same conditions of pressure and temperature will contain the same number of molecules. This is known as Avogadro’s hypothesis.

Law Of Equipartion Of Energy
Degrees of freedom:
Degrees of freedom is number of independent ways by which a molecule can possess kinetic energy of translation, rotation and vibration.

Law of equipartition energy:
The total kinetic energy of a molecule is equally divided among the different degrees of freedom.

K.E. per degree of freedom:
The average energy per degree of freedom

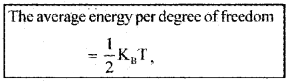
Where K_B is Boltzman constant.

Degrees of freedom and energy of monoatomic gas:
A monoatomic atom has 3 degrees of freedom, ie; it can move in x, y and z-direction. The average energy of single monoatomic gas in the x-direction,

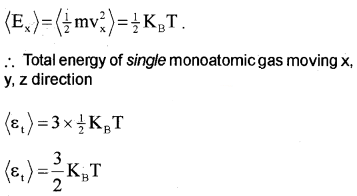
Note:
1. If a molecule is restricted to move in plane. It has 2 degrees of freedom.
2. If a molecule is restricted to move in a line, it has only 1 degrees of freedom.

Degrees of freedom and energy of single diatomic molecule (rigid rotator)

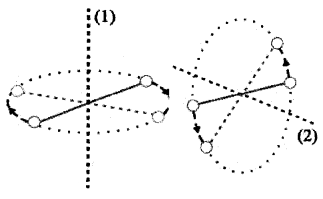
Consider a diatomic molecule as a rigid rotator (Rigid rotator means that the molecule does not vibrate). A rigid diatomic molecule has 3 translation degrees of freedom and 2 rotational degrees of freedom.
(Rotational degrees of freedom is shown in the above figure).
∴ Total average energy of diatomic rigid rotator,

Note:
A diatomic molecule has 3 rotational degrees of freedom. But we consider only 2 degrees of freedom. We neglect rotation along the line joining the atoms. Because it has very small moment of inertia.

Degrees of freedom and energy of single diatomic molecule of nonrigid rotator:
Molecules like ‘co’ even at moderate temperatures have a mode of vibration. The vibration energy of a diatomic molecule.

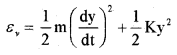
Where K is the force constant of the oscillator and y the vibrational coordinate. The vibration energy mode contain two terms (1) Kinetic energy (2) Potential energy. Hence a single mode of vibration of molecule is considered as 2 degrees of freedom (potential energy and kinetic energy)
∴ The total vibrational energy of a single-mode
= 2 × \(\frac{1}{2}\)K_BT
= K_BT
∴ The total energy of diatomic nonrigid rotator

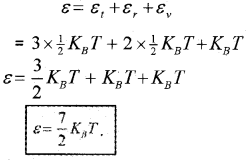
Degrees of freedom and energy of polyatomic molecule, (non- rigid rotator):
If a polyatomic molecule has ‘f’ modes of vibration, total number of degrees freedom = 3 vibration + 3 rotator+f vibration.
∴ Total average energy of single polyatomic molecule,

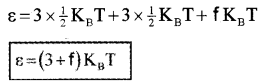
Specific Heat Capacity
Monoatomic Gases (Molar specific heat capacity):
The energy of a single monoatomic gas = 3 × \(\frac{1}{2}\) K_BT
The energy of one mole monoatomic gas = 3 × \(\frac{1}{2}\) K_BT × N_A
[one-mole atom contain Avogadro number (N_A) of atoms]

A Diatomic Gas (Molar specific heat capacity):
A rigid diatomic molecule has 5 degrees of freedom : 3 translational and 2 rotational.
∴ energy of single diatomic (rigid) molecule = 5 × \(\frac{1}{2}\) K_BT
for one mole of diatomic molecule, energy U = 5 × \(\frac{1}{2}\) K_BT × N_A

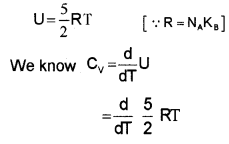
Nonrigid diatomic molecule having a vibrational mode (Molar specific heat capacity):
If the diatomic molecule is not rigid but has a vibration mode. The energy of one mole,

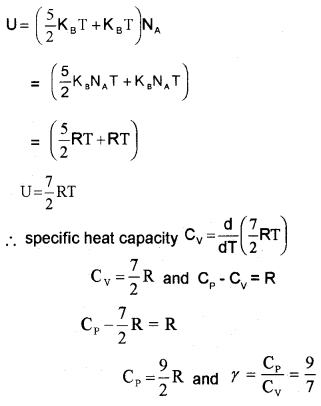
Polyatomic Gas (Molar specific heat capacity):
In general a polyatomic molecule has 3 translational, 3 rotational degrees of freedom and a certain number (t) of vibrational modes.

The energy of one mole polyatomic gas,

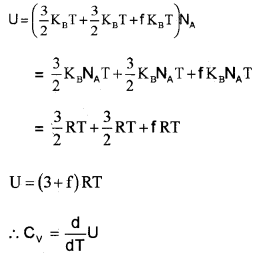
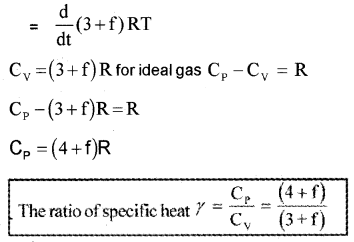
Note: The experimental value of C_P and C_V of polyatomic gases are greater than the predicted values. The theoretical value and experimental value will be equal when we include vibrational modes of motion in the calculation.

Specific heat capacity of solids:
Consider a solid of N atoms. Each atom is vibrating about its mean position. Each vibration mode has two degrees of freedom (corresponding to potential energy and kinetic energy). Hence an oscillation in one dimension has average energy of

2 × \(\frac{1}{2}\) K_BT = K_BT
∴ Total energy in three dimension
= 3 × K_BT
= 3K_BT.

For one mole of solid, total energy,
U = 3K_BT × N_A
[N_A = Avagadro number]
= 3N_AK_BT
U = 3RT …………………. (1) [∴ R = K_BN_A].
We know specific heat capacity,

Note:
In solids, we do not consider the translational and rotational degrees of freedom. We consider only vibrational degrees of freedom.

Specific heat capacity of water:
We treat water like a solid. A water molecule has 3 atoms. Each atom in the molecule is vibrating about its mean position. A single vibration mode has 2 degrees of freedom (1) potential energy (2) kinetic energy.

ie; The energy of one atom in one dimensional vibration mode =
2 × \(\frac{1}{2}\) K_BT = K_BT

The energy of one atom having 3 dimensional vibration mode = 3 × K_BT
The energy of one H₂0 molecule having 3 dimension vibration mode
U = 3 × 3K_BT × N_A
U = 9RT [∵ R = K_B N_A]
∴ Specific heat capacity,
\(\mathrm{c}=\frac{\mathrm{dU}}{\mathrm{dT}}=\frac{\mathrm{d}}{\mathrm{dT}}(\mathrm{RT})\)
C = 9R.

Mean Free Path
Molecules in a gas have large speeds. Yet a gas leaking from a cylinder in a kitchen takes considerable time to diffuse to the other corners of the room. Why?

The molecules in a gas have a finite size. So they collide with other molecules during their motion. As a result, they cannot move straight like path. Their paths are continuously deflected.

Mean free path:
The mean free path is the average distance covered by a molecule between two successive collisions.

Expression for mean free path:

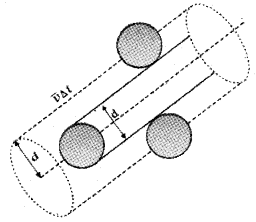
Suppose the molecules of a gas are spheres with diameterd. Let 〈v〉 be the average velocity of the molecule.
The volume covered by a molecule during its motion, in a time Δt = πd² 〈v〉 Δt.
If ‘n’ is the number of molecules per unit volume, the total number of molecules in the above volume
= πd² 〈v〉 Δt n.
The number collisions in a time Dt,
= πd² 〈v〉 Δt n.
Number of collisions in one second,
= n π d² 〈v〉
∴ The time between two successive collisions,
\(\tau=\frac{1}{n \pi d^{2}\langle v\rangle}\).
The average distance between two successive collisions,

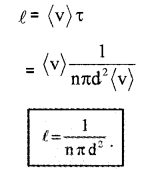
In this derivation, we imagined the other molecules to be rest. But actually, all other molecules are moving. Hence we must take relative velocity 〈v_r〉 instead of 〈v〉. A more exact treatment gives
\(\ell=\frac{1}{\sqrt{2} \mathrm{n} \pi \mathrm{d}^{2}} \dots(1)\)
The mean free path given by the above equation depends inversely on the number density and the size of the molecule.

Plus One Physics Notes