Plus One Physics Notes Chapter 10 Mechanical Properties of Fluids

Kerala Plus One Physics Notes Chapter 10 Mechanical Properties of Fluids

Summary
Introduction
Unlike a solid, a fluid has no definite shape. Fluid is that which can flow. Liquids and gases are fluids. A fluid has no definite shape. It assumes the shape of the container.
Difference between the liquids and gases:

• Liquid is incompressible, while a gas is compressible.
• Liquid has a free surface, while a gas no free surface.

Common properties of liquids and gases:

• Liquids and gases can flow
• Liquids and gases can exert pressure on the walls of the container.

Pressure
In fluids, the molecules are free to move. When they move, they collide with the walls of the container and exert a force on the walls. The force is acting normal to the surface. The force acting per unit area normal to the surface is called pressure.

ie; P = F/A. Its unit is N/m² or Pascal (Pa), Another common unit of pressure is atmosphere. The pressure exerted by the atmosphere at sea level is called the atmospheric pressure.
I atm = 1.0313 × 10⁵Pa
Properties of Fluid Pressure:

• The pressure will be equal at any point on the same horizontal level of a liquid at rest.
• The pressure will be the same in all directions at any point in a liquid at rest.

Question 1.
When a surface is immersed in a liquid, what is the direction of pressure on the surface?

Answer:
The direction of pressure is always normal to the surface.
Density:
The density r for a fluid of mass m occupying volume V

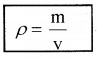
The density of water at 4°C (277k) is 1 × 10³kg m^-3
Relative density:
The relative density of a substance is the ratio of its density to the density of water at 4°C. The relative density of aluminium is 2.7. Its density is 2.7 × 10³kg m^-3.
1. Variation of pressure with Depth:

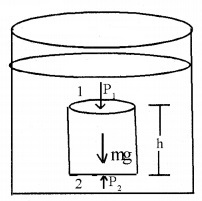
Consider a fluid at rest in a container. Consider a cylindrical element of fluid having base area ‘A’ and height ‘h’. Let P₁ and P₂ be pressures at points 1 and 2 respectively.
The force at top of cylindrical element F₁ = P₁A
This force is acting vertically down ward.
Similarly, the force at bottom F₂ = P₂A
This force is acting vertically upward.
∴ Total force acting on the cylindrical element of fluid = P₂A – P₁A
The fluid is at rest. Hence, Net force on the cylindrical element of fluid = Weight of cylindrical element of fluid.
ie.: (P₂ – P₁)A = mg
(P₂ – P₁)A = vρg (∴ m = ρv)
(P₂ – P₁)A = Ahρg (∴ v = Ah)
P₂ – P₁ = hρg _____(1)
The above equation shows that pressure difference depends on the vertical distance h between the points (1 and 2), density of the fluid, acceleration due to gravity.
Gauge Pressure:
If the point 1 is shifted to the top of fluid, P₁ may be replaced by atmospheric pressure ‘P_a’. Let pressure at bottom of cylindrical element be ‘P\ then from eq (1), we can write
P – P_a = hρg
P = P_a + hρg
The above equation shows that, the pressure P (below the surface of a liquid open to the atmosphere) is greater than atmospheric pressure by an amount rgh. The excess pressure (P – P_a) at depth h is called guage pressure.

Hydrostatic paradox:
Question 2.
In which points (see figure) pressure is maximum?

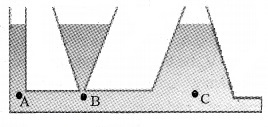
Answer:
The liquid pressure is the same at all points (A, B, C). Because all the points lie at same horizontal level. The pressure at A, B and C do not depend upon base area or shape of the container. This paradox is called hydrostatic paradox.

2.  Atmospheric pressure and Gauge pressure:
Atmospheric pressure:
The pressure exerted by the atmosphere at any point is due to the weight of air above that point. At sea level the atmospheric pressure is maximum and is taken as 1 atmosphere.
1 atm = 1.013 × 10⁵ Pa
Mercury Barometer:
Italian scientist Evangelista Torricelli (1608 -1647) devised a method for measuring atmospheric pressure. This device is known as mercury barometer.

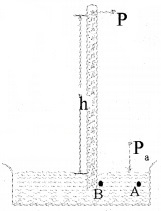
A long glass tube closed at one end is filled with mercury. Then it is inverted in a mercury reservoir. The mercury level inside the tube falls up to a height 76 cm.

Consider two points A and B in the reservoir. Since the reservoir is open to the atmosphere, the pressure at,
P₀ = P_a (atmospheric pressure).
The pressure at B is P_B = Hrg
The points A and B lie at same level, hence
pressure at A = pressure at B
P_a = P_B
ie; P_a = Hrg
In the experiment, it is found that the mercury column in the barometer has a height of about 76 cm at sea level. 76 cm of mercury = 1 atm.
Different unit of pressure:
1 mm of mercury = 1 torr
1 torr= 133 Pa
1 bar= 10⁵ Pa
Open – Tube Manometer:

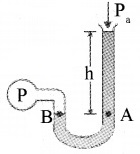
open-tube manometer is a useful instrument for measuring pressure differences. This device consists of a U shaped tube containing liquid of density r. One end is open to the atmosphere and other end is connected to the system whose pressure is to be measured.

The pressure ‘P’ at A is equal to the pressure at B.
ie: P = P_a + hρg
(or) P – P_a = hρg
P is called absolute pressure.

3. Hydraulic Machines:
Hydraulic machines are based on Pascal’s law. Examples of hydraulic machines:

• Hydraulic Lift
• Hydraulic press
• Hydraulic brake.

Pascal’s Law:
Whenever external pressure is applied on any part of a fluid contained in a vessel, it is transmitted undiminished and equally in all directions.

Hydraulic lift:

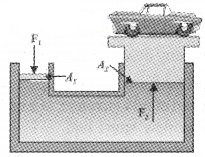
A hydraulic lift is used to lift heavy load. Consider a liquid enclosed in a vessel with two cylinders C₁ and C₂ attached as shown in the figure. The cylinders are provided with two pistons having areas A₁ and A₂ respectively.
If F₁ is the force exerted on the area A₁.
pressure P₁ = \(\frac{F_{1}}{A_{1}}\)
If F₂ is the force exerted on the area A₂,
pressure P₂ = \(\frac{F_{2}}{A_{2}}\)
According to pascal’s law P₁ = P₂ ie;

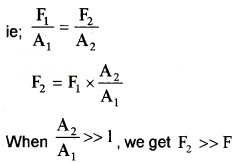
Using this method we can lift heavy load by applying small force.
Hydraulic Brake:

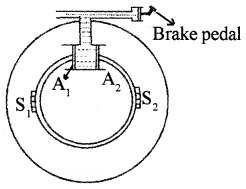
Hydraulic brake is based on Pascals law. When the brake pedal (F) is pressed, a pressure is produced on liquid. This pressure will reach at A₁ and A₂. Due to large area of A₁ and A₂, a large force is produced. This large force will push brake shoes (S₁ ans S₂) in to the inner rim of wheel. Hence the motion of wheel will be retarded.

Streamline Flow
Fluid dynamics:
The study of the fluids in motion is known as fluid dynamics.
Steady Flow:
The flow of the fluid is said to be steady if at any given point, the velocity of each fluid particle remains constant in time. The path taken by a fluid particle under a steady flow is a streamline.
Turbulent flow:
As the speed of flow increase, at a certain speed the stream line flow stops and irregular flow starts. This irregular flow is called turbulent.

The speed at which the turbulent flow starts is called critical speed.
Equation of continuity:
Flow rate of a incompressible fluid is constant
ie Av = cont.
Where A is the area of cross section of flow and v is the velocity of flow. ‘Av’ is also called volume flux.
Proof:
Consider a flow of incompressible liquid. Let P, R and Q be three points of a flow. Consider three planes perpendicular to direction of flow at P, R and Q.

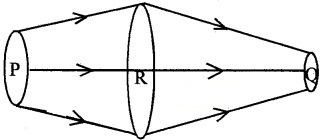
Let A_P, A_R and A_Q be the area of cross section and V_P, V_R and V_Q be the corresponding speeds at P, R, Q respectively.
The mass of liquid passing through area A_P in a time Dt, M_P = A_P V_P r_P ∆t
Similarly, M_R = A_R V_R r_R ∆t
M_Q = A_Q V_Q r_Q ∆t
But we know r_P = r_R = r_Q = r
Hence we get M_P = A_P V_P r ∆t
M_R = A_R V_Rr ∆t
M_Q = A_Q V_Q r ∆t
the mass of liquid flowing out = the mass flowing in
ie; M_P = M_R = M_Q
∴ A_PV_P = A_RV_R = A_QV_Q

Bernoulli’S Principle
Bernoulli’s theorem:
As we move along a streamline the sum of the pressure (p), the kinetic energy per unit volume \(\frac{\rho v^{2}}{2}\) and the potential energy per unit volume (ρgh) remains a constant.

(OR)

The total energy of an incompressible non-viscous liquid flowing from one place to another without friction is a constant. Mathematically Bernoulli’s theorem can be written as

Proof:

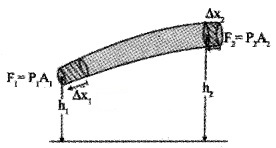
Consider an incompressible liquid flowing through a tube of non uniform cross section from region 1 to region 2. Let P₁ be the pressure, A₁ the area of cross section and V₁ the speed of flow at the region 1.

The corresponding values at region 2 are P₂, A_2, and V₂ respectively. Region 1 is at a height h₁ and region 2 is at a height h₂.
The workdone on the liquid in a time ∆t at the region 1 is given by
W₁ = force × distance
= P₁A₁∆ x₁
= P₁∆V₁ (∵ A₁∆x₁ = ∆V)
Where ∆x₁ is the displacement produced at region 1, during the time interval ∆t.
Similarly, the workdone in a time ∆t at the region 2 is given by,
W₂ = -P₂ A₂ ∆ x₂
W₂ = -P₂ ∆ V₂
[Here -ve sign appears as the direction of \(\vec{p}\) and ∆x are in opposite directions.]
Net workdone
DW = P₁ ∆ V₁ – P₂ ∆ V₂
According the equation of continuity
∆V₁ = ∆V₂ = ∆V
∆W= P₁ ∆ V – P₂ ∆ V
∆W = (P₁ – P₂) ∆ V _____(1)
This work done changes the kinetic energy, pressure energy and potential energy of the fluid.
If ∆m is the mass of liquid passing through the pipe in a time ∆t. the change in Kinetic energy is

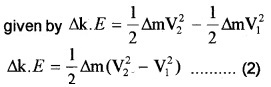
Change in gravitational potential energy is given by
∆p.E = ∆mgh₂ – ∆mgh₁
∆p.E = ∆mg(h₂ – h₁) ______(3)
According to work-energy theorem work done is equal to the change in kinetic energy plus the change in potential energy.
ie; ∆w = ∆kE + ∆PE ______(4)
Substituting eq. 1, 2 and 3 in eq. 4, we get

Dividing by ∆V , we get

Case – 1
When the fluid at rest, its velocity is zero everywhere. Hence Bernoullis equation becomes
p₁ + ρgh₁ = P₂ + ρgh₂
(P₁ – P₂) = ρg(h₂ – h₁ )
Note: Bernoullis law is conservation law of energy for a flowing liquid.

1. Speed of Afflux: Torricellis law:
Torricellis law may be stated as the velocity of afflux through a hole at a depth ‘h’ will be equal to the velocity gained by a freely falling body when it travels a distance ‘h’. ie; v = \(\sqrt{2 \mathrm{gh}}\).
Proof
Consider a tank containing a liquid of density r with a small hole in its side. Let Y₁ be the height of the hole, and y₂ be height of water in the tank. Applying Bernoullis equation at points (1) and (2) we get

(∵ P₁ = P_a, the atmospheric pressure).
If the cross sectional area of the tank A₂ is much larger than that of the hole (ie; A₂ >> A₁ ), we take
v₂ ≈ 0.
∴ eq(1) can be written as.

Note: The equation (2) shows that the speed of afflux is determined by the container pressure. Such a situation occurs in rocket propulsion.

2. Venturi – meter:

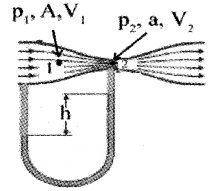
A venturi meter is used to measure the flow of a liquid. It is based on Bernoulli’s theorem. Venturimeter consists of a horizontal tube of the nonuniform cross-section. A manometer (U tube) is attached to it as shown in the figure.

When a liquid flows through the tube, the manometer level falls in the limb (1) and rises in the limb (2). Let ‘h’ be the height difference of the manometer liquid in the two limbs. Let A be the cross-sectional area and V₁ the velocity at the wide limb(1) and V₂ be the corresponding values at the narrow limb (2).
According to Bernoulli’s theorem

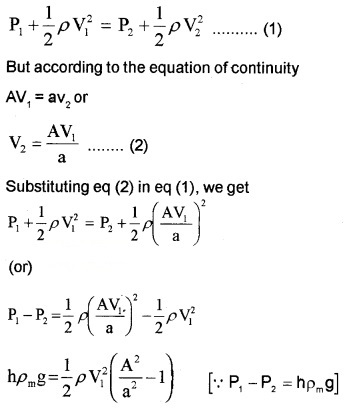
Where ρ_m is the density of manometer liquid.

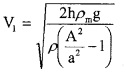
Using the above equation, the rate of flow can be measured.
Atomiser (application of Bernoulli’s theorem):

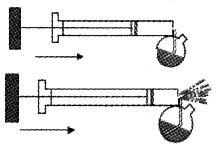
Atomiser is used for getting a fine spray of perfumer or insecticide. It consists of a cylinder with a piston. A small vessel containing liquid to be sprayed is attached to the cylinder. When the piston is moved forward air is blown out through a small opening of the cylinder.

As the velocity of flow of air increases, the pressure at the opening decreases. Due to the lower pressure at the opening, the liquid rises through the narrow tube and gets sprayed out along with air.

Blood flow and heart attack:
Bernoulli’s principle helps in explaining blood flow in artery. The artery may get constricted due to the accumulation of plaque on its inner walls. The speed of blood flow increases at which plaque is deposited. The increase in speed will lowers the pressure inside the artery and it may collapse due to the external pressure. This may result in heart attack.

4. Dynamic lift:
Dynamic lift is the force that acts on a body by virtue of its motion through a fluid (air). (This dynamic lift can be partly explained on the basis of Bernoulli’s principle)
Example:

1. Ball moving without spin
2. Ball moving with spin
3. Aerofoil or lift on aircraft wing.

1. Ball moving without spin:

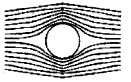
When a ball move in air without spinning, the velocity of fluid (air) above and below the ball is the same. Hence pressure difference between above and below is zero. Therefore there is no upward or downward force on the ball.

2. Ball moving with spin:

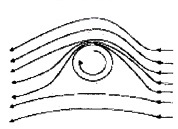
When a ball is thrown in a air with spin, air will be dragged along with it. Therefore the velocity of air above (larger) and below (smaller) are different. This difference in the velocities of air results in the pressure difference between the lower and upper faces and there is a net upward force on the ball. This dynamic lift due to spinning is called Magnus effect.

3. Aerofoil or lift on aircraft wing:

An aerofoil is a solid piece, shaped to provide an upward vertical force as it moves horizontally through air. Due to the curved shape at the top, the velocity of the air on the top side increases. Due to increase in velocity, the pressure at this region decreases. Thus an upward force develops on the aerofoil. This principle is applied in the design of the wings of aeroplanes.

Viscosity
Viscosity is liquid friction. When liquid layer moves over another liquid layer, there is a force of friction between the liquid layers, opposing the motion of layers.

Laminar flow:
When a liquid flows on a surface, the layer of liquid in contact with the surface will be rest. The velocity of the layer increases as the distance of the layer from the surface increases. The velocity is maximum on the top most layer. This type of flow is known as laminar.

Coefficient of viscosity:
The coefficient of viscosity for a fluid is defined as the ratio of shearing stress to the strain rate. Explanation:

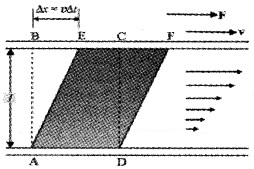
Consider a portion of liquid having shape ABCD. When this liquid flows, it take the shape AEFD after a short interval of time Dt
During this time interval the liquid has undergone a shear strain of \(\frac{\Delta \mathbf{x}}{\ell}\). Since, the stress in a flowing fluid increases with time, we take rate.
ie. strain rate = \(\frac{\Delta \mathbf{x}}{\ell \Delta t}\)

Unit of viscosity:
The SI unit of viscosity is poiseiulle (PI). Its another units are NSm^-2 or PaS.
Note:

• Blood is thicker (more viscous) than water. The relative viscocity (n/n_water) of blood remains constant between 0° C and 37° C.
• The viscocity of liquid decreases with temperature while it increases in the case of gases.

1. Stokes law:
If a body is moving through a fluid, its velocity is influenced by the viscosity of the medium. Consider a small sphere of radius ‘a’ falling under gravity in air: The viscocity of air opposes the motion of the sphere. This opposing force is called viscous force and can be written as.
F = 6πaηv
This is called stokes, formula.
Where η is the coefficient of viscocity of the medium and v is the velocity of the body.

(i) Terminal velocity:
The constant velocity attained by a body as it falls down through a fluid medium is called the terminal velocity.
Expression for terminal velocity:
Considers sphere of radius ‘a’ densitity r falling through a liquid of density s and viscocity h. The viscous force acting on the sphere can be written as
F = 6πaηv
Where v is the velocity of sphere. This force is acting in upward direction. When the body comes down its velocity will increase. Hence the viscous force will also increases.

When the viscous force is equal to the weight of the body in the medium. The net force on the body is zero. Now the body falls without acceleration. It moves with a constant velocity called the terminal velocity.
The weight of a body in a medium,

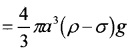
When body has terminal velocity, we can write.

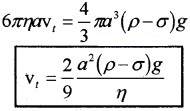
Reynolds Number
The turbulence in a fluid is determined by a dimension parameter called Reynolds number.
Reynolds number R_e = \(\frac{\rho \mathbf{v d}}{\eta}\)
Where ‘r is the density of a fluid, V- the speed of flow of the liquid, ‘d’- the dimension of pipe, h- viscocity of the liquid. R_e – the dimensionless number. The flow is streamlined when the R_e is below 1000, unsteady when R_e is in between 1000 and 2000 and turbulent when R_e > 2000.
Critical velocity:
The maximum velocity of a fluid in a tube for which the flow remains streamlined is called its critical velocity.
Critical velocity v = \(\frac{R_{e} \eta}{\rho d}\).

Surface Tension
Liquids acquire a free surface when poured in a container. These surfaces possess some additional. energy. This phenomenon is known as surface tension.

1. Surface Energy:
Question 4.
What is the reason for surface tension?

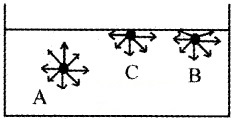
Answer:
Consider a liquid enclosed in a vessel as shown in figure. Let A, B, and C be three molecules in the liquid. For a molecule A, the forces of attraction on the molecule are equal in all directions. Hence net force on it is zero. Consider a molecule B near the surface. In this case the molecule is partially outside the liquid. So there is a net downward force.

Consider another molecule Con the surface of liquid. Half of the sphere is outside the liquid. Hence the downward force on molecule is maximum. This, when a molecule comes to the surface, it is doing work to overcome this downward pull. The work done resides as RE. in the molecule on the surface. Thus molecule on the surface of liquid has P.E. This energy is called the surface energy.
Note:
1. To increase the area of surface of a liquid, work has to be done. This energy is required to increase the surface area.

2. Surface energy and surface tension:
Question 5.
Show that Surface tension is equal to surface energy per unit area.

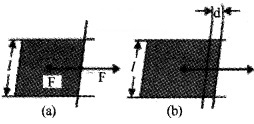
Answer:
Consider a horizontal liquid film as shown in figure. The bar at one end of film is free to move. Move the bar a small distance as shown in figure. Since the area of the surface increases, some work has to be done against an internal force.
workdone W = Fd _____(1)
This workdone is stored as additional energy in the film. If the surface energy of the film is S per unit area, the workdone to increase the surface area.
W = S × increase in area
W = S × 2/d ______(2)
Where 2/d is the increase in area due to two sides of film.
equating eq(1) and eq(2),we get
S 2/d = Fd
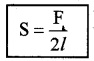“Plus One Physics Notes Chapter 10 Mechanical Properties of Fluids 34″ width=”94″ height=”61” />
This quantity S is the magnitude of surface tension. It is equal to the surface energy per unit area.

3. Angle of contact:
Angle of contact is the angle between the solid surface and the tangent drawn to the liquid surface at the point of contact inside the liquid.

If angle of contact of liquid is acute(<90°), the meniscus in the tube will be concave. The liquid level in the tube will rise to a certain height. This is called capillary rise. If the angle of contact is obtuse (>90°), the liquid level falls in the tube. This is called capillary fall or capillary depression.

4. Drops and bubbles:
Due to surface tension, the liquid surface always tends to have the minimum surface area. For a given volume, a sphere has a minimum surface area. Hence, srnail drops and bubbles of a liquid assume spherical shape.

On the other hand, for bigger drops the effect of gravity predominates over surface tension and the drop gets flattened.

(i) Excess of pressure inside a spherical drop The molecules near the surface of a drop experience a resultant pull inwards due to surface tension. Because of this inward pull, the pressure inside is greater than the outside.

Due to the forces of surface tension, the drop tends to contract. But due to excess inside pressure, the drop tends to expand. When the drop is in equilibrium, these two forces will be equal and opposite.

Expression for excess pressure inside a liquid-drop:

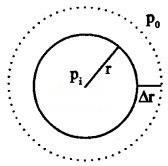
Consider a drop of liquid of radius r. Let p_i and p_o be the values of pressure inside and outside the drop. Let the radius of liquid of drop increases by a small amount Dr under the pressure difference.
The outward force acting on the surface of the drop,
f = pressure difference × surface area,
ie. f = (p_i – p_o)4pr²
If the radius of liquid drop is increased by Dr due to the above force
The work done (DW) = f.Dr
= (p_i – p_o)4pr²Dr _____(1)
The increase in surface area of the drop
= 4p(r + Dr)² – 4pr²
= 4p(r² + 2rDr + Dr²) – 4pr² = 8prDr [ Neglecting Dr²]
If S is the surface tension of the liquid, the work done to increase the surface area,
DW = Increase in surface area × surface tension
DW= 8prDr.S _____(2)
From equation (1) and (2), we get 2S
p_i – p_o = \(\frac{2 \mathrm{S}}{\mathrm{r}}\).

(ii) Expression for excess pressure inside a spherical bubble:
A liquid bubble has air both inside and outside it. Hence, it has two surfaces;
Hence the total increase in the surface area, = 16prDr
The workdone to increase the surface area,
= 16prDrS ______(3)
From equation (1) and (3) we get,
p_i – p_o = \(\frac{4 \mathrm{S}}{\mathrm{r}}\)

5. Capillary rise:
A tube of very fine core is called a capillary tube. When a capillary tube is dipped in a liquid, the liquid immediately rises in the tube. This phenomenon is called capillarity or capillary rise. In the case of mercury, capillary depression is observed.
Expression for capillary rise:

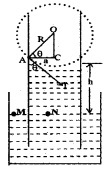
Consider a capillary tube of radius ‘a’ dipped in a liquid of density rand surface tension S. If the liquid has a concave meniscus it will rise in the capillary tube. Let h be the rise of the liquid in the tube. Let p₁ be the pressure on the concave Side of the meniscus and p₀, that on the other side.
The excess pressure on the concave side of the meniscus can be written as
p_i – p_o = \(\frac{2 \mathrm{S}}{\mathrm{r}}\) _____(1)
Where R is the radius of the concave meniscus. The tangent to the meniscus at point A makes an angle q with the wall of the tube.
In the right angled triangle ACO

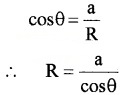
substituting the values of R in the equation (1)

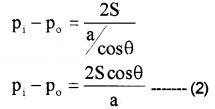
Considering two points M and N in the same horizontal level of a liquid at rest,
pressure at N = pressure at M
But pressure at M = p_i, the pressure over the concave meniscus and pressure at N = p_o + hrg
∴ p_o = p_o + hrg
or p_i – p_o = hrg ______(3)
From equations (2) and (3), we get
hρg = \(\frac{2 \mathrm{S} \cos \theta}{\mathrm{a}}\)

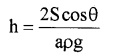
case-1
For water q = 0, ie. cos q = 1
hence S = \(\frac{1}{2}\) haρg

6. Detergents and Surface Tension:
Dirty clothes containing grease and oil stains sticking on them cannot be cleaned by soaking them in water. This is because water will not wet greasy dirt. If water could wet grease, then the flow of water would carry away some greasy dirt.

But, by adding detergent or soap to water, the greasy dirt can be removed. The molecules of the detergent are hairpin shaped. When the detergent is added to water, one end of hair pin shaped molecule get attached to the water surface and other end to stain.

This results in the formation of water – grease interface. Thus surface tension between water and grease reduces. Hence dirt can be removed by the moving water.

Plus One Physics Notes