Kerala Plus One Physics Improvement Question Paper Say 2018 with Answers
| Board | SCERT |
| Class | Plus One |
| Subject | Physics |
| Category | Plus One Previous Year Question Papers |
Time: 2 Hours
Cool off time: 15 Minutes
Maximum: 60 Scores
General Instructions to candidates:
- There is a ‘cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read the instructions carefully.
- Read questions carefully before you answering.
- Calculations, figures, and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non-programmable calculators are not allowed in the Examination Hall.
Answer any 4 questions from question numbers 1 to 5. Each carry 1 score. (4 × 1 = 4)
Question 1.
State TRUE or FALSE
“Some conservation laws are true for one fundamental force, but not for the others”.
Answer:
True
Question 2.
The angle between A = i + j and B = i – j is
a) 45°
b) 90°
c) 60°
d) 180°
Answer:
b) 90°
Question 3.
Three objects with a mass of 40kg each are placed in a straight line 50cm apart. What is the net gravitational force at the centre object due to the other two?
Answer:
Zero
Question 4.
Which one of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
a) a = 5x
b) a = -200x2
c) a = -5x
d) a = 100x3
Answer:
c) a = – 5x
Question 5.
The stress required to double the length of a wire of Young’s modulus Y is ………..
a) Y/2
b) 2Y
c) y
d) 4Y
Answer:
c) y
Answer any 4 questions from question numbers 6 to 10. Each carries 2 scores. (4 × 2 = 8)
Question 6.
A car travelling at a speed 54 km/hr is brought to rest in 90s. Find the distance travelled by the car before coming to rest.
Answer:

Question 7.
The parallelogram law is used to find the resultant of two vectors. Find the magnitude of the resultant of two vectors in terms of their magnitudes and angle between them.
Answer:
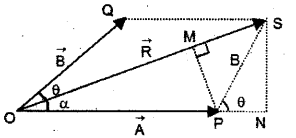
Consider two vectors \(\overrightarrow{\mathrm{A}}\) (\(=\overrightarrow{\mathrm{OP}}\)) and B (\(=\overrightarrow{\mathrm{OQ}}\)) making an angle θ. Using the parallelogram method of vectors, the resultant vector R can be written as,
\(\overrightarrow{\mathrm{R}}\) = \(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\)
SN is normal to OP and PM is normal to OS. From the geometry of the figure
OS2 = ON2 + SN2
but ON = OP + PN
ie. OS2 = (OP + PN)2 + SN2 ……..(1)
From the triangle SPN, we get
PN = Bcosθ and SN = Bsinθ
Substituting these values in eq.(1), we get
OS2 = (OP + Bcosθ)2 + (Bsinθ)2

Question 8.
Select the CORRECT alternative.
a) When a conservative force does positive work on a body, the potential energy of the body……….
i) increases
ii) decreases
iii) remains unaltered
b) Work done by a body against friction always results in a loss of its……..
i) kinetic energy
ii) potential energy
c) The rate of change of total momentum of a system of many particle system is proportional to the ……… on the system.
i) external force
ii) sum of the internal forces
d) The quantity which is conserved in an inelastic collision of two bodies is …….
i) total kinetic energy
ii) total linear momentum
Answer:
a) decreases
b) kinetic energy
c) external force
d) total linear momentum
Question 9.
A steel wire of length 1.5 m and diameter 0.25 cm is loaded with a force of 98 N. The increase in length of the wire 1.5 × 10-4 m. Calculate the tensile stress and the fractional change in length of the wire.
Answer:

Question 10.
According to the kinetic theory of gases, gas molecules are always in random motion.
a) State the law of equipartition of energy.
b) Write the average value of energy of a molecule for each vibrational mode.
Answer:
a) The total kinetic energy of a molecule is equally divided among the different degrees freedom.
b) E = \(\frac{1}{2}\)KBT × 2 = KBT
Answer any 4 questions from question numbers 11 to 15. Each carries 3 scores. (4 × 3 = 12)
Question 11.
Two parallel rail tracks run north-south. Train A moves north with a speed of 15 m/s and train B moves south with a speed of 25 m/s.
a) What is the velocity of B with respect to A?
b) What is the velocity of ground with respect to B?
c) What is the velocity of a monkey running on the roof of the train A against its motion (with a velocity of 5m/s with respect to the train A) as observed by a man standing on the ground?
Answer:
a) VBA = VB – -VA = 25 + 15 = 40 m/s
b) VgB = Vg – VB = 0 – 25 = -25 m/s
Resultant velocity = 15 – 5
(opposite to direction) = 10 m/s
Question 12.
An insect trapped in a circular groove of radius 12cm moves along the groove steadily and completes 7 revolutions in 100s.
a) What is the linear speed of the motion?
b) Is the acceleration vector a constant vector? What is its magnitude?
Answer:
a) R = 12 × 10-2m
7 revolutions = 100 sec
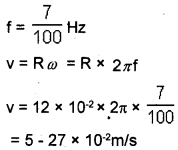

Question 13.
A car and a truck have the same kinetic energies at a certain instant while they are moving along two parallel roads.
a) Which one will have greater momentum?
b) If the mass of truck is 100 times greater than that of the car, find the ratio of velocity of the truck to that of the car.
Answer:

Question 14.
A girl rotates on a swivel chair as shown below.

a) What happens to her angular speed when she stretches her arms?
b) Name and state the conservation law applied for your justification.
Answer:
a) The angular speed decreases
b) Law of conservation of angular momentum. According to this law, the angular momentum of a body is conserved when external torque is zero.
Question 15.
A solid sphere of mass m and radius R starts from rest and rolls down along an inclined plane of height h without slipping as shown below:
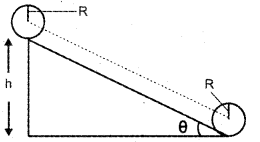
a) Calculate the kinetic energy of the sphere when it reaches the ground
b) Find the velocity when it reaches the base.
Answer:
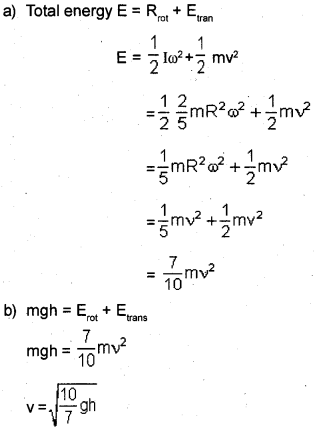
Answer any 4 questions from question numbers 16 to 20. Each carries 4 scores. (4 × 4 = 16)
Question 16.
A man jumping out of a slow moving bus falls forward.
a) This is due to ……..
b) Which Newton’s law gives the above concept? State the law.
c) What is the net force acting on a book at rest on the table?
Answer:
a) Inertia/inertia of motion
b) First law of Newton. The law states that every body continues its state of rest or uniform motion along straight line unless it is compelled by an. external unbalanced force to change that state.
c) Zero
Question 17.
To reduce friction and accident by skidding, the roads are banked at curves.
a) What is meant by banking of roads?
b) Sketch the schematic diagram of a vehicle on a banked road with friction and mark the various forces.
c) Derive an expression for maximum safe speed of a vehicle on a banked road with friction.
Answer:
a) Theputeredgeofthe road is raised slightly above the inner edge. This is called banking of road.
b)
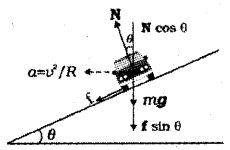
c) Consider a vehicle along a curved road with angle of banking q. Then the normal reaction on the ground will be inclined at an angle q with the vertical.
The vertical component can be divided into N ‘ Cosq (vertical component) and N sinq (horizontal component). Suppose the vehicle has a tendency to slip outward. Then the frictional force will be developed along the plane of road as shown in the figure. The frictional force can be divided into two components. Fcosq (horizontal component) and F sinq (vertical component).
From the figure are get
N cosθ = F sinθ + mg
N cosθ – F sinθ = mg ……..(1)
The component Nsinθ and Fsinθ provide centripetal force. Hence

This is the maximum speed at which vehicle can move over a banked curved road.
Question 18.
For a liquid-gas interface, the convex side has a high pressure than the concave side.
a) Derive an expression for excess pressure inside a drop.
b) Which is better, washing of cloth in cool soap water or warm soap water? Why?
Answer:
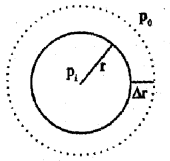
Consider a drop of liquid of radius r. Let Pi and Po be the values of pressure inside and outside the drop.
Let the radius of liquid of drop increases by a small amount Dr under the pressure difference.
The outward force acting on the surface of the drop, f = pressure difference × surface area,
ie. f = (pi – po)4pr2
If the radius of liquid drop is increased by Dr due to the above force
Theworkdone(DW) = f.Dr
= (Pi – Po)4pr2Dr ……….(1)
The increase in surface area of the drop
= 4p(r + Dr)2 – 4pr2
= 4p(r2 + 2rDr + Dr2) – 4pr2 = 8prDr
[ Neglecting Dr2]
If S is the surface tension of the liquid, the workdone to increase the surface area,
DW = Increase in surface area × surface tension
DW = 8prDr.S ………(2)
From equation (1) and (2), we get
Pi – Po = \(\frac{2 \mathrm{~S}}{\mathrm{r}}\)
b) Warm soap water, because temperature reduces surface tension.
Question 19.
Linear expansion is change in length of an object with temperature.
a) Write the equation for coefficient of linear expansion.
b) Show that the coefficient of volume expansion is thrice its coefficient of linear expansion.
c) The absolute zero is……..
-273.15°C, -273.15K, -273.15°F, 0°C,
Answer:
a) α = \(\frac{\Delta \ell}{\ell \Delta T}\)
b) Consider a cube of length ‘l’. Due to the increase in temperature ‘ΔT’, length of cube increases by Δl in all directions.
Coefficient of linear expansion, αl = \(\frac{\Delta \ell}{\ell \Delta \mathrm{T}}\)
Increase in area of cube ΔA
= Final area – initial area
= (l + Δl)2 – l2 = 2 × l × Δl
[Neglecting Δl2]
Area expansivity
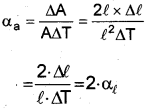
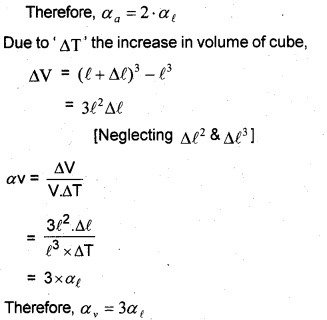
c) -273.15°C
Question 20.
The simplest example of simple harmonic motion is the oscillations of a simple pendulum.
a) Derive an expression for the period of oscillation of a simple pendulum.
b) In a simple pendulum made of a metallic wire, what will happen to the period when temperature increases? Give a reason.
Answer:
a)
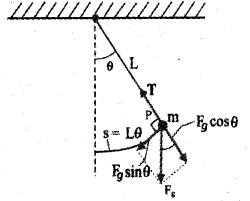
Consider a mass m suspended from one end of a string of length L fixed at the other end as shown in figure. Suppose P is the instantaneous position of the pendulum. At this instant its string makes an angle θ with the vertical.
The forces acting on the bob are (1) weight of bob Fg (mg) acting vertically downward. (2) Tension T in the string.
The gravitational force Fg can be divided into a radial component FgCosθ and tangential component FgSinθ. The radial component is cancelled by the tension T. But the tangential component FgSinθ produces a restoring torque.
Restoring torque τ = – Fg sinθ.L
τ = -mgsinθ.L ………(1)
-ve sign shown that the torque and angular displacement θ are oppositely directed. For rotational motion of bob,
τ = Iα ……….(2)
Where I is moment of inertia about the point of suspension and α is angular acceleration. From eq (1) and eq (2).
Iα = – mgsinθ.L
If we assume that the displacement θ is small, sinθ ≈ θ.
∴ Iα = – mgθ.L

b) Period increases because as temperature increases length of metal wire also increases.
Answer any 4 questions from question numbers 21 to 25. Each carries 5 scores. (4 × 5 = 20)
Question 21.
a) The centripetal force depends on mass of the body, velocity and radius of circular path. Find the expression for the centripetal force acting on the body using the principle of dimensional analysis. (Take constant k = 1)
b) When the planet Jupiter is at a distance of 824.7 million kilometers from the Earth, its angular diameter is measured to be 35.72″ of arc. Calculate the diameter of the Jupiter.
Answer:
a) The centripetal force depends on mass (m), radius (r) and velocity (v)
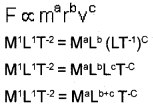
Equating we get
a = 1
b + c = 1
c = 2
∴ b = -1

Question 22.
Satellites are objects which revolve around the earth.
a) The direction of revolution of geosynchronous satellite is from ……….
i) east to west
ii) west to east
iii) north to south
iv) south to north
b) Derive an expression for total energy of an orbiting satellite.
c) What is the magnitude of the angular velocity for a geosynchronous satellite?
Answer:
a) West to east
b) The kinetic energy of the satellite in a circular orbit at height h from surface of earth with speed

Question 23.
The flow of an ideal fluid in a pipe of varying cross section is shown below.
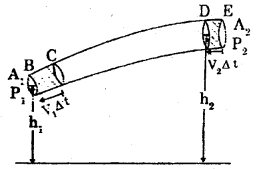
a) Write Bernoulli’s equation.
b) Find the speed of efflux using Bernoulli’s principle.
c) StateTorricelli’s law.
Answer:
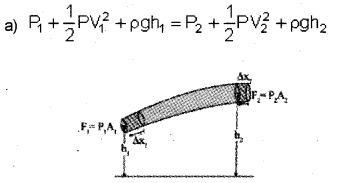
Consider an incompressible liquid flowing through a tube of non uniform cross section from region 1 to region 2. Let P1 be the pressure, A1 the area of cross section and V1 the speed of flow at the region 1. The corresponding values at region 2 are P2, A2 and V2 respectively. Region 1 is at a height h, and region 2 is at a height h2.
The workdone on the liquid in a time Δt at the region 1 is given by
W1 = force × distance
= P A1Δx1
= P1ΔV1
(∵A1Δx1 = ΔV)
Where Δx1 is the displacement produced at region 1, during the time interval Δt Similarly the workdone in a time Δt at the region 2 is given by,
W2 = -P2 A2 Δx2
W2 = -P2ΔV2
[Here -ve sign appears as the direction of \(\overrightarrow{\mathrm{p}}\) and Δx are in opposite directions.]
Net workdone
DW = P1ΔV1 – P2ΔV2
According the equation of continuity
ΔV1 = ΔV2 = ΔV
∴ ΔW= P1ΔV – P2ΔV
ΔW = (P1 – P2)ΔV ……….(1)
This work done changes the kinetic energy, pressure energy and potential energy of the fluid.
If Δm is the mass of liquid passing through the pipe in a time Δt. the change in Kinetic energy is given by Δk.E = \(\frac{1}{2} \Delta \mathrm{mV}_{2}^{2}-\frac{1}{2} \Delta \mathrm{mV}_{1}^{2}\)
Δk.E = \(\frac{1}{2} \Delta \mathrm{m}\left(\mathrm{V}_{2}^{2}-\mathrm{V}_{1}^{2}\right)\) ……….(2)
Change in gravitational potential energy is given by
Δp.E = Δmgh2 – Δmgh1.
Δp.E= Δmg(h2 – h1) ……….(3)
According to work-energy theorem work done is equal to the change in kinetic energy plus the change in potential energy.
ie; Δw = ΔkE + ΔPE ……….(4)
Substituting eq. 1, 2 and 3 in eq. 4, we get
\(\left(P_{1}-P_{2}\right) \Delta V=\frac{1}{2} \Delta m\left(V_{2}^{2}-V_{1}^{2}\right)+\Delta m g\left(h_{2}-h_{1}\right)\)

b) Consider a tank containing a liquid of density r with a small hole in its side. Let Y1 be the height of the hole, and y2 be height of water in the tank. Applying Bernoulli’s equation at points (1) and (2) we get
![]()
(∵P1 = Pa, the atmospheric pressure).
If the cross sectional area of the tank A2 is much larger than that of the hole (ie; A2>>A1), we take
v2 ≈ 0
∴ eq(1) can be written as.

c) Torricelli’s law may be stated as the velocity of afflux through a hole at a depth ‘h’ will be equal to the velocity gained by a freely falling body when it travels a distance ‘h’.
ie; v = \(\sqrt{2 \mathrm{gh}}\)
Question 24.
The basic features of a device are schematically represented in the figure below.
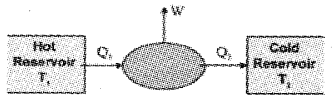
a) Which type of device is this, a heat engine or a refrigerator?
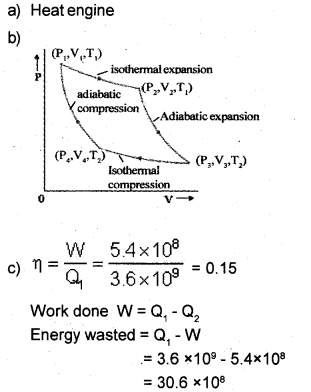
b) Draw the indicator diagram and label the four processes in the Carnot cycle.
c) A steam engine delivers 5.4 × 108J of work per minute and services 3.6 × 109J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
Answer:
Question 25.
A transverse harmonic wave on a string is described by y(x, t) = 3.0 Sin(36t + 0.018x + π/4) where ‘x’ and ‘y’ are in cm and ‘t’ is in s. The positive direction of ‘x’ is from left to right.
a) Is this a travelling wave or a stationary wave? If it is travelling, what are the speed and direction of its propagation?
b) What are its amplitude and frequency?
c) What is the least distance between two successive crests in the wave?
Answer:
