Kerala Plus One Physics Chapter Wise Questions and Answers Chapter 4 Motion in a Plane
Plus One Physics Motion in a Plane One Mark Questions and Answers
Question 1.
A cricketer can throw a ball to a maximum horizontal distance of 100m. With the same speed how much high above the ground can the cricketer throw the same ball?
(a) 200m
(b) 150m
(c) 100m
(d) 50m
Answer:
(d) 50m
Rmax = \(\frac{u^{2}}{g}\)
100 = \(\frac{u^{2}}{g}\) or u2 = 100g
Using, v2 = u2 + 2as
0 = (100g) + 2(-g)h or h = 50m.
Question 2.
If vectors \(\hat{\mathrm{i}}-3 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}\) and \(\hat{\mathrm{i}}-3 \hat{\mathrm{j}}-\mathrm{ak}\) are equal vectors, then the value of a is
(a) 5
(b) 2
(c) -3
(d) -5
Answer:
(d) Comparing vector, we get = \(+5 \hat{k}=-a \hat{k}\)
a = -5.
Question 3.
State which of the following algebraic operations are not meaningful
(a) Addition of a scalar to a vector
(b) Multiplication of any two scalars.
(c) Multiplication of vector by scalar
(d) Division of a vector by scalar Addition of a scalar to a vector
Answer:
(a) Addition of a scalar to a vector
Question 4.
What is the acceleration of train travelling at 40ms-1 as it goes round a curve of 160m radius?
Answer:
a = \(\frac{v^{2}}{r}=\frac{40 \times 40}{160}\) = ms-2.
Question 5.
What provides centripetal force in the following cases.
- Electron revolving around nucleus.
- Earth revolving around sun
Answer:
- Electrostatic force
- Gravitational force
Question 6.
Why a cyclist has to bend inwards while going on a circular track?
Answer:
The cyclist bends inwards to provide required centripetal force.
Question 7.
A body executing uniform circular motion has constant
(i) velocity
(ii) acceleration
(iii) speed
(iv) angular velocity
Answer:
(iii) speed
Question 8.
Name a quantity which remains unchanged during projectile motion.
Answer:
Horizontal component.
Question 9.
What is the effect of air resistance in time of flight and horizontal range?
Answer:
The effect of air resistance is to increase time of flight and decrease horizontal range.
Question 10.
What is the angle between directions of velocity and acceleration at the highest point of trajectory of projectile?
Answer:
At the highest point velocity is horizontal and acceleration is vertical. So angle is 90°.
Question 11.
Can a body have constant velocity and still have a varying speed?
Answer:
No.
If velocity is constant, speed also will be constant.
Question 12.
Can a body have zero velocity, still accelerating?
Answer:
Yes.
When a body is at highest point of motion, its velocity is zero but acceleration is equal to acceleration due to gravity.
Question 13.
A quantity has both magnitude and direction. Is it necessarily a vector? Give an example.
Answer:
No. The given quantity will be a vector only if it obeys laws of vector addition.
Example: Current.
Question 14.
What is the angle between \(\vec{A} \times \vec{B}\) and \(\vec{B} \times \vec{A}\) ?
Answer:
These two vectors will be antiparallel. Hence θ = 180°.
Plus One Physics Motion in a Plane Two Mark Questions and Answers
Question 1.
A particle is projected with a velocity u so that its horizontal range is twice the greatest hieght attained. The horizontal range is
(a) \(\frac{u^{2}}{g}\)
(b) \(\frac{2 u^{2}}{g}\)
(c) \(\frac{4 u^{2}}{5g}\)
(d) None of these
Answer:
(c) Horizontal range, R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\);
Maximum height, H = \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
As per question, R = 2H
![]()
or sin2θ = sin2θ
or 2sinθcosθ = sin2θ or tanθ = 2
Hence, sinθ = \(\left(\frac{2}{\sqrt{5}}\right)\) and cosθ = \(\left(\frac{1}{\sqrt{5}}\right)\)
Horizontal range, R = \(\frac{2 u^{2} \sin \theta \cos \theta}{g}\)
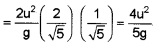
Question 2.

Answer:

Question 3.
Choose the correct alternative given below. A Particle executing uniform circular motion. Then its
(a) Velocity and acceleration are radial.
(b) Velocity and acceleration are tangential.
(c) Velocity is tangential, acceleration is radial.
(d) Velocity is radial, acceleration is tangential.
(e) In a circus, a rider rides in a circular track of radius Y in a vertical plane. The minimum velocity at the highest point of the track will be
- \(\sqrt{2 g r}\)
- \(\sqrt{ g r}\)
- \(\sqrt{3 g r}\)
- 0
Answer:
(c) Velocity is tangential, acceleration is radial.
(e) \(\sqrt{ g r}\)
Question 4.
Two non-zero vectors \(\bar{A}\) and \(\bar{B}\) are such that \(|\bar{A}+\bar{B}|=|\bar{A}-\bar{B}|\). Find the angle between them.
Answer:
\(|\bar{A}+\bar{B}|=|\bar{A}-\bar{B}|\)
|A2 + B2 + 2ABcosθ| = |A2 + B2 – 2ABcosθ|
|4ABcosθ| = 0
Since A and B are non-zero we get, cos θ = 0 or θ = 90°.
Question 5.
Consider a particle moving along the circumference of a circle of radius R with constant speed with a time period T.
- During T, what is the distance coverd and displacement?
- What is the direction of the velocity at each point?
Answer:
- Distance = 2πR. Displacement = 0
- Tangent to the circle at every point.
Question 6.
Classify into scalars and vectors. Frequency, velocity gradient, instantaneous velocity, Area.
Answer:
| Scalars | Vectors |
| Frequency | Instantaneous velocity |
| Velocity gradient | Ares |
Question 7.
A body is projected so that it has maximum range R. What is the maximum height reached during the fight?
Answer:
At maximum range, θ = 45°
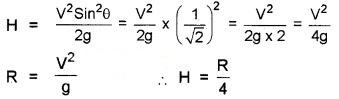
Plus One Physics Motion in a Plane Three Mark Questions and Answers
Question 1.
An electron of mass ‘m’ moves with a uniform speed v around the nucleus along a circular radius Y.
- Derive an expression for the acceleration of the electron.
- Explain why the speed of electron does not increase even though it is accelerated by the above acceleration.
Answer:
1.
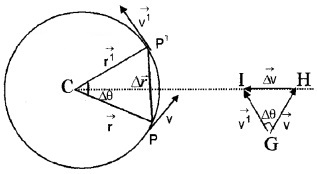

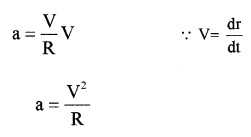
The acceleration is directed towards the centre of the circle and is called centripetal acceleration.
a0 = \(\frac{v^{2}}{R}\)
But V = Rω
Substituting we get
ac = Rω2
2. The direction of centripetal force is towards the centre. The angle between force and displacement is 90°. Hence the work done by the centripetal force is zero. So speed does not increase.
Question 2.
A boy pulls his friend in a home made trolley by means of a rope inclined at 30° to the horizontal. If the tension in the rope is 400N.
- Draw the vertical and horizontal components of tension in the rope.
- Find the effective force pulling the trolley along the ground.
- Find the force tending to lift the trolley off the ground.
Answer:
1.
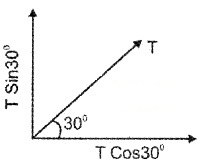
2. Effective horizontal force = T Cos30°
= 400 × Cos 30°
3. Vertical force = T Sin 30°
= 400 × Sin 30°
Question 3.
A stone tied to the end of a string is whirled in a horizontal circle with constant speed.
- Name the acceleration experienced by the stone.
- Arrive at an equation for magnitude of acceleration experienced by the stone.
Answer:
1. Centripetal acceleration
2.
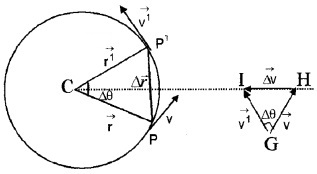

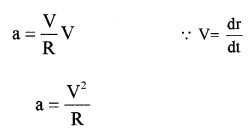
The acceleration is directed towards the centre of the circle and is called centripetal acceleration.
a0 = \(\frac{v^{2}}{R}\)
But V = Rω
Substituting we get
ac = Rω2
Plus One Physics Motion in a Plane Four Mark Questions and Answers
Question 1.
Two balls are released simultaneously from a certain height, one is allowed to fall freely and other thrown with some horizontal velocity.
- Will they hit the ground together?
- At any time during the fall will the velocities of the balls are same?
- How does the path of the balls appear to a person standing on the ground?
Answer:
- Both balls will reach at same time.
- Total velocity of first body and second body is different. First ball has only downward velocity but second ball has both downward and horizontal velocity.
- The path of first ball appears to be straight line and that of second ball appears to be parabola.
Question 2.
A ball is thrown straight up.
- Obtain a mathematical expression for the height to which it travels.
- What js its velocity and acceleration at the top?
- Draw the velocity-time graph for the ball showing its motion up and down.
Answer:
1. u = u, v = o, a = -g, h = ?
We can find maximum height using the equation
v2 = u2 + 2as
0 = u2 + 2 × – g × H
2gh = u2
H = \(\frac{u^{2}}{2 g}\)
2. Velocity is zero, but it has a acceleration and its value g = 9.8 m/s2.
3.
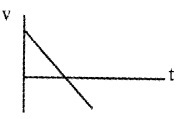
Question 3.
- Parallelogram law helps to find the magnitude and direction of the resultant of two forces. State the law.
- For two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) are acting at a point with an angle a between them, find the magnitude and direction of the resultant vector.
- What will be the angle between two vectors of equal magnitude for their resultant to have the same magnitude as one of the vectors?
Answer:
1. Law of parallelogram of vectors:
If two vectors acting simultaneously at a point are represented in magnitude and direction by the two adjacent sides of a parallelogram then the diagonal of the parallelogram passing through that point represents the resultant in magnitude and direction.
2.
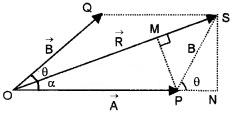
Consider two vectors \(\vec{A}(=\overrightarrow{O P}) \text { and } \vec{B}(=\overrightarrow{O Q})\) making an angle θ. Using the parallelogram method of vectors, the resultant vector R can be written as,
![]()
SN is normal to OP and PM is normal to OS. From the geometry of the figure
OS2 = ON2 + SN2
but ON = OP + PN
ie. OS2 = (OP+PN)2 + SN2 ______(1)
From the triangle SPN, we get
PN = Bcosθ and SN = Bsinθ
Substituting these values in eq.(1), we get
OS2 = (OP + Bcosθ)2 + (Bsinθ)2
But OS = R and OP = A
= A2 + 2ABcosθ + B2cos2θ + B2sin2θ
2 = A2 +2 ABcosθ + B2
R = \(\sqrt{A^{2}+2 A B \cos \theta+B^{2}}\)
The resultant vector \(\overrightarrow{\mathrm{R}}\) make an angle a with \(\overrightarrow{\mathrm{R}}\). From the right angled triangle OSN,
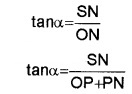
But SN = Bsinθ and PN = Bcosθ
3. 120°
Question 4.
A ball of mass m is projected at an angle with the ground and it is found that its kinetic energy at the highest point is 75% of that at the point of projection.
- Is it a one-dimensional or a two-dimensional motion? Why?
- Find the angle of projection
- Determine another angle of projection which produces the same range.
Answer:
1. Two-dimensional motion. The projectile has two dimensions.
2. The K.E at highest point
Ek = E cos2θ,
where E = initial K.E
0.75 E = E cos2θ
cos2θ = 0.75 = 3/4
cosθ = \(\sqrt{3} / 2\)
θ = 60°
3. When an object is projected with velocity ‘u’ making an angle θ to with the horizontal direction, the horizontal range will be
R1 = \(\frac{u^{2} \sin 2 \theta}{g}\) ____(1)
when an object is projected with velocity u making an angle (90° – θ) with the horizontal direction, then horizontal range will be
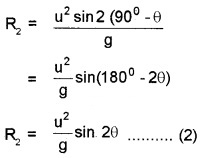
From eq (1) eq (2), we get R1 = R2, which means that we get same horizontal range for two angles θ and (90 – θ).
Question 5.
“The graphical method of adding vectors helps us in visualizing the vectors and the resultant vector. But, sometimes, it is tedious and has limited accuracy”.
- Name the alternative method of vector addition.
- Write a mathematical expression to find resultant of two vectors.
- A particle is moving eastward with a velocity of 5m/s. |f in 10s, the velocity changes by 5 m/s northwards, what is the average acceleration in this time.
Answer:
1. Analytical method of vector addition.
2. R = \(\sqrt{A^{2}+B^{2}+2 A B \cos \theta}\)
3. Change in velocity
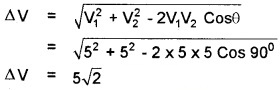
Average acceleration
Question 6.

Answer:
Question 7.
A projectile is an object projected into air with a velocity V so that it is moving under the influence of gravity.
- What is the shape of the path of projectile?
- As a projectile moves in its path, is there any point along the path where the velocity and acceleration vectors are perpendicular to each other
- If E is energy with a projectile is projected.
(i) What is the Kinetic energy at the highest point.
(ii) What is P.E at highest point?
Answer:
1. Parabola
2. Yes, highest point
3. Energy with a projectile is projected:
(i) Kinetic energy Ek = 1/2mv2
Velocity at the highest point = Vcosθ
∴ K.E. at highest point = 1/2m(Vcosθ)2
= 1/2 mv2cos2θ
K.E. = Ek cos2θ
(ii) Potential energy at highest point,
P.E. = mgh
= mg\(\frac{v^{2} \sin ^{2} \theta}{2 g}\) = 1/2mv2sin2θ
P.E. = Ek sin2θ.
Plus One Physics Motion in a Plane Five Mark Questions and Answers
Question 1.
An object is projected with velocity U at an angle θ to the horizontal.
- Obtain a mathematical expression for the range in the horizontal plane.
- What are the conditions to obtain maximum horizontal range?
- Find the maximum height of the object when its path makes an angle of 30° with the horizontal (velocity of projection = 8 ms-1)
Answer:
1. If we neglect the air resistance, the horizontal velocity (ucosθ) of projectile will be a constant. Hence the horizontal distance (R) can be found as
R = horizontal velocity × time of flight

2. when θ = 45° we get maximum horizontal range
3. Height H
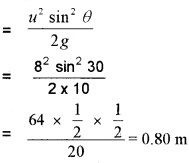
Question 2.
The path of projectile from A is shown in the figure. M is the mass of the particle.
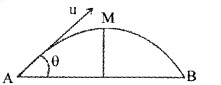
When the particle moves from A to M.
- a) What is the change in vertical velocity?
- b) What is the change in speed?
- What is the change in linear momentum?
- The ceiling of a long hall is 25m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 ms-1 can go without hitting the ceiling of the hall?
Answer:
1.
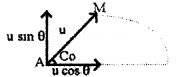
When the particle reaches at M, the vertical component of velocity becomes zero.
change in vertical velocity = u sinθ – 0
= u sinθ
2. change in speed = u cosθ – u
3. change in momentum = mu sinθ – 0
= mu sinθ
4.
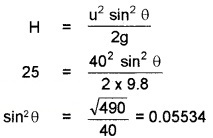
θ = 33°481
The horizontal range of the ball is
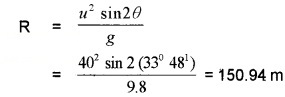
Question 3.
A particle moving uniformly along a circle, experiences a force directed towards the centre and an equal and opposite force directed away from the centre.
- Name the two forces directed towards and away from the centre.
- Obtain an expression for the force directed towards the centre.
- An aircraft executes a horizontal loop at a speed of 720 km hr-1 with its wings banked at 15°. What is the radius of the loop?
Answer:
1. centripetal force and centrifugal force.
2.

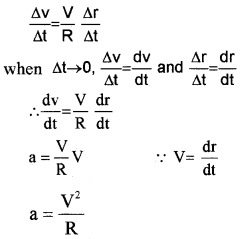
force which produces this centripetal acceleration is called centripetal force.
Centripetal force can be written as F = ma.
F = m\(\frac{V^{2}}{R}\)
3. Speed of aircraft, 720 × \(\frac{5}{18}\) = 200 m/s
The velocity of aircraft, ν = \(\sqrt{r g \tan \theta}\)
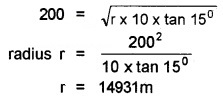
Question 4.
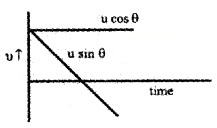
A body is projected with a velocity ‘u’ in a direction making an angle θ with the horizontal.
- Derive the mathematical equation of the path followed.
- Draw the velocity-time graphs for the horizontal and vertical components of velocity of the projectile.
- Obtain an expression for the time of flight of the projectile.
Answer:
1. The vertical displacement of projectile at any time t, can be found using the formula.
S = ut + 1/2at2
y = usinθt – 1/2gt2
But we know horizontal displacement,
x = ucosθxt
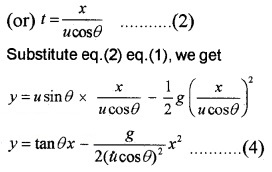
In this equation g, θ and u are constants. Hence eq.(4) can be written in the form
y = ax + bx2
where a and b are constants. This is the equation of parabola, ie. the path of the projectile is a parabola.
2.
3. The time taken by the projectile to cover the horizontal range is called the time of flight.
Time of flight of projectile is decided by usinθ. The time of flight can be found using the formula s = ut + 1/2 at2
Taking vertical displacement s = 0, a = -g and initial vertical velocity = usinθ, we get
0 = usinθt – 1/2gt2
1/2 gt2 = usinθt
t = \(\frac{2 u \sin \theta}{g}\).
Question 5.
An object projected into air with a velocity is called a projectile.
- What will be the range when the angle of projections are zero degrees and ninety degrees?
- Show that fora projectile, the upward time of flight is equal to the downward time of flight.
- At what angles will a projectile have the same range fora velocity?
Answer:
1. When θ = 0°
R = 0
When θ = 90°
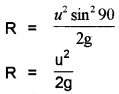
2. Upward motion
u = u sinθ, a = -g, v = 0
V = u + at
0 = u sinθ + –gt
ta = \(\frac{u \sin \theta}{g}\) ____(1)
Downward motion
u = 0, V= u sinθ, a = +g
V = u + at
u sinθ = 0 + gt
ta = \(\frac{u \sin \theta}{g}\) ____(2)
eq (1) and (2), shows up ward time of flight is equal to downward time of flight.
3. θ, 90 – θ.
Question 6.
“An object that is in flight after being thrown or projected is called a projectile”.
1. Which of the following remains constant throughout the motion of the projectile?
(i) Vertical component of velocity
(ii) Horizontal component of velocity
2. Derive an expression for maximum range of a projectile.
3. Show that range of projection of a projectile for two angles of a projection a and (3 is same where α + β = 90°.
Answer:
1. (ii)
2. If we neglect the air resistance, the horizontal velocity (ucosθ) of projectile will be a constant. Hence the horizontal distance (R) can be found as
R = horizontal velocity × time of flight

3. Range of projectile R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\)
Case – 1
at angle α,
Rα = \(\frac{\mathrm{u}^{2} \sin 2 \alpha}{\mathrm{g}}\) ____(1)
Case – 2
at an angle β,

From (1) and (2), we get
Rα = Rβ
Question 7.
A bullet is fired with a velocity ‘u’ at an angle ‘θ’ with the horizontal such that it moves under the effect of gravity.
- What is the nature of its trajectory.
- Arrive at an expression for time of flight of the bullet.
- What is the relation between time of ascent and time of decent, when air resistance is neglected.
- How the relation is affected when air resistance is considered.
Answer:
1. Parabola
2. The time taken by the projectile to cover the horizontal range is called the time of flight. Time of flight of projectile is decided by usinθ. The time of flight can be found using the formula s = ut + 1/2 at2
Taking vertical displacement s = 0, a = -g and initial vertical velocity = usinθ, we get
0 = usinθt – 1/2gt2
1/2 gt2 = usinθt
t = \(\frac{2 u \sin \theta}{g}\).
3. Time of ascent = time of descent
4. Time of descent > time of ascent
Plus One Physics Motion in a Plane NCERT Questions and Answers
Question 1.
State for each of the following physical quantities, if it is a scalar or a vector:
Volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.
Answer:
- Scalars: Volume, mass, speed, density, number of moles and angular frequency.
- Vectors: acceleration, velocity, displacement, and angular velocity.
Question 2.
Pick out the two scalar quantities in the following list: force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.
Answer:
Work, current.
Question 3.
State, with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
- Adding any two scalars.
- Adding a scalar to a vector of the same dimensions
- Multiplying any vector by any scalar
- Multiplying any two scalars
- Adding any two vectors
- Adding a component of a vector to the same vector.
Answer:
- No. Scalars must represent same physical quantity.
- No. Vector can be added only to another vector.
- Yes. When a vector is multiplied by any scalar, we get a vector.
- Yes. In multiplication, scalars may not represent the same physical quantity.
- No. The two vectors must represent the same physical quantity.
- Yes. The vector and its component must have the same dimensions.
Question 4.
Pick out the only vector quantity in the following list: temperature, pressure, impulse, time, power, total path length, energy, gravitational potential, coefficient of friction, charge.
Answer:
Impulse.
Question 5.
Read each statement below carefully and state with reasons, if it is true or false:
- The magnitude of a vector is always a scalar.
- Each component of a vector is always a scalar.
- The total path length is always equal to the magnitude of the displacement vector of a particle.
- The average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater or equal to the magnitude of average velocity of the particle over the same interval of time.
- Three vectors not lying in a plane can never add up to give a null vector.
Answer:
- True
- False
- False
- True
- True.
In order to give a null vector, the third vector should have the same magnitude and opposite direction to the resultant of two vectors.
Question 6.
A cyclist starts from the centre O of a circular park, then cycles along the circumference, and returns to the centre along QO as shown. If the round trip takes 10 minutes, what is the
- Net displacement.
- Average velocity and
- Average speed of the cyclist?
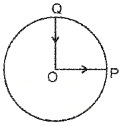
Answer:
1. Since both the initial and final positions are the same therefore the net displacement is zero.
2. Average velocity is the ratio of net displacement and total time taken. Since the net displacement is zero therefore the average velocity is also zero.
3. Average Speed
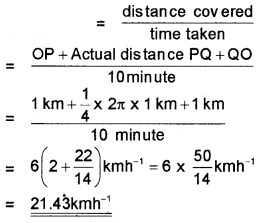
Question 7.
A passenger arriving in a new town wishes to go from the station to hotel located 10km away on a straight road from the station. A dishonest cabman takes him along a circuitous path 23 km long and reaches the hotel in 28 minute, what is
- The average speed of the taxi
- The magnitude of average velocity? Are the two equal?
Answer:
Magnitude of displacement = 10km
Total path length = 23km
Time taken = 28 min
![]()
Average Speed = \(\frac{23 \mathrm{km}}{\frac{7}{15} \mathrm{h}}\)
= 49.3 kmh-1
Magnitude of average velocity
