Plus One Physics Chapter Wise Questions and Answers Chapter 14 Oscillations

Kerala Plus One Physics Chapter Wise Questions and Answers Chapter 14 Oscillations

Plus One Physics Oscillations One Mark Questions and Answers

Question 1.
Fill in the blanks :
A girl is swinging on a swing in a sitting position. When she stands up, the period of the swing will______.
Answer:
Decreases

Question 2.
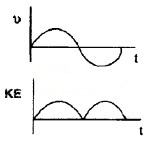
A particle executes a simple harmonic motion with a frequency f. What is the frequency with which its kinetic energy oscillates?
Answer:
The frequency of oscillation of kinetic energy is 2f.

Question 3.

Answer:
a. 7/2R
b. ω = \(\sqrt{k / m}\)

Question 4.
Can a simple pendulum vibrate at centre of earth?
Answer:
No. Because ‘g’ at centre of earth is zero.

Question 5.
A glass window may be broken by a distant explosion. Why?
Answer:
The sound waves can cause forced vibrations in glass due to difference between frequency of sound wave and natural frequency of glass. This can break the glass window.

Plus One Physics Oscillations Two Mark Questions and Answers

Question 1.
A simple pendulum is transferred from earth to moon. Will it go faster or slower?
Answer:
The value of g at moon is low compared to earth. The decrease in g will increase time period of simple pendulum. Hence pendulum will vibrate slower.

Question 2.
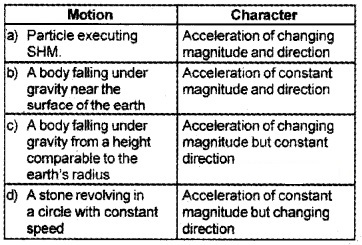
Here five examples of accelerated motion are given in first column. Match each examples given in the second column.

Answer:

Question 3.
A girl is swinging a swing in sitting position. What shall be the effect of frequency of oscillation if

1. if she stands up
2. if another girl sits gently by her side

Answer:
1. If the system is considered a simple pendulum, length of pendulum is reduced as girl stands up.

So frequency of oscillation is increased.

2. The time period and hence frequency of simple pendulum is independent of mass. Hence there is no change in frequency.

Plus One Physics Oscillations Three Mark Questions and Answers

Question 1.
A student is advised to study the variation of period of oscillation with the length of a simple pendulum in the laboratory. According he recorded the period of oscillation for different lengths of the pendulum.

1. If he plots a graph between the length and period of oscillation, what will be the shape of the graph?
2. How would you determine the value of acceleration due to gravity using l – T² graph?

Answer:
1.

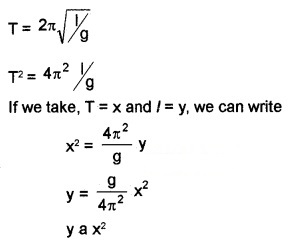
This is the equation parabola. Hence the shape of graph between period(T) and length (l) will be parabola.

2. Find slope of l – T² graph. The acceleration due to gravity can be found using formula g = 4P² × slope of (l – T²) graph.

Question 2.
A simple pendulum has a bob of mass m is suspended from the ceiling of a lift which is lying at the ground floor of a multistoried building.

1. Find the period of oscillation of pendulum when the lift is stationary.
2. What is the tension of the string of the pendulum when it is ascending with an acceleration ‘a’?
3. What is the period of oscillation of the pendulum while the lift is ascending?

Answer:

1. T = \(2 \pi \sqrt{l /g}\)
2. Tension, T= m (g + a)
3. T = 2π\(\sqrt{\frac{\ell}{g+a}}\)

Question 3.
A body tied a spherical pot with a string and suspended it on a clamp. He then filled it with water. Length of the string if 90 cm and diameter of the pot is 20 cm. The pot is slightly displaced to one side and leave it to oscillate. Considering the above example as a simple pendulum (g = 9.8 ms^-2)

1. What is the length of the Pendulum
2. Calculate the period of oscillation of the pendulum.

Answer:
1. Length of pendulum l = 90 + 10 = 100 cm

2.

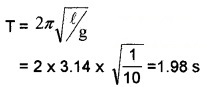
Question 4.

1. Motion repeated at regular intervals of time is called periodic. Explain the simple harmonic motion with a figure.
2. A particle executes a simple harmonic motion with a period 2 seconds, starting from its equilibrium at time t = 0. Find the minimum time in which it is displaced by half the amplitude.

Answer:
1. A periodic motion in which acceleration is directly proportional to displacement but opposite in direction is called SHM.

The graphical variation of simple harmonic motion with time given above.

2. y = a sin wt

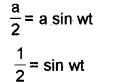
Sin π/6 = sin wt
wt = π/6
\(\frac{2 \pi}{T}\)t = π/6
But T = 2s. Hence we get

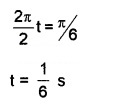
Question 5.
A spring of spring constant ‘k’ is used to suspend a mass ‘m’ at its free end while the other end of the spring is rigidly fixed.

1. If the mass is slightly depressed and released, then name the motion of the mass.
2. Write down the expression for the period of oscillation of the mass.
3. If this system is taken into outer space then what happens to its period? Why?

Answer:

1. Simple Harmonic Motion
2. T = \(2 \pi \sqrt{m / k}\)
3. Period of oscillation does not change.

Plus One Physics Oscillations Four Mark Questions and Answers

Question 1.
A simple harmonic motion is represented by x(t) = Acosωt.

1. What do you mean by simple harmonic motion.
2. An SHM has amplitude A and time period T, What is the time taken to travel from x = A to x = A/2

Answer:
1. Simple harmonic motion is the simplest form of oscillatory motion. The oscillatory motion is said to be simple harmonic motion if the displacement ‘x’ of the partide from the origin varies with time as

2. x = Acosωt

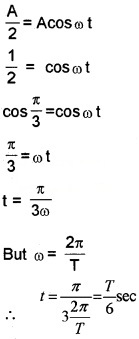
Question 2.

1. Define simple harmonic motion for a particle moving in a straight line.
2. Use your definition to explain how simple harmonic motion can be represented by the equation.
3. Show that the above equation is dimensionally correct.
4. A mechanical system is known to perform simple harmonic motion. What quantity must be measured in order to determine frequency for the system?

Answer:

1. A periodic motion in which acceleration is directly proportional to displacement and opposite in direction is called simple harmonic oscillation.
2. Mathematically, a simple harmonic oscillation can be expressed as
   y = a sin wt (or) y = a cos wt
3. y = a sin w t
   Sin wt has no dimension. Hence we need to consider dimension of ‘a’ only, ie, y = a, L = L
4. Its period is determined.

Question 3.
A particle executes simple harmonic motion according to the equation x = 5sin\(\left(\frac{2 \pi}{3} t\right)\)

1. find the period of the oscillation
2. What is the minimum time required for the particle to move between two points 2.5cm on either side of the mean position?

Answer:
1. x = 5sin\(\left(\frac{2 \pi}{3} t\right)\), when we compare this equation
with standard S.H.M, x = a sin wt.
We get wt = \(\frac{2 \pi}{3} t\)

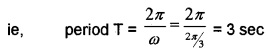
2. y = a sin wt
2.5 = 5 sin w × t

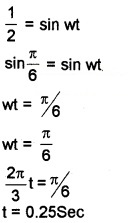
Time taken to travel 2.5 from the mean position is 0.25 sec. Hence time taken to travel 2.5 cm on either side of the mean position is 0.5 sec.

Question 4.
A mass m is suspended at one end of a spring and the other end of the spring is firmly fixed on the ceiling. If the mass is slightly depressed and released it will execute oscillation.

1. Write down the expression for the frequency of oscillation of the mass.
2. If the spring is cut into two equal halves and one half of the spring is used to suspend the same mass then obtain an expression for the ratio of periods of oscillation in two cases.
3. If this system is completely immersed in water then what happens to the oscillation?

Answer:
1. f = \(\frac{1}{2 \pi} \sqrt{k / m}\)

2. f₁ = [atex]\frac{1}{2 \pi} \sqrt{k / m}[/latex] ____(1)

3. When spring is cut into half spring constant becomes 2k. Hence frequency,

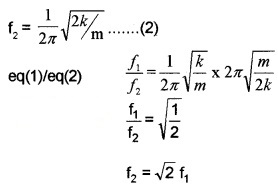
4. If this system is immersed in water, the amplitude of oscillation decrease quickly. Hence system comes to rest quickly.

Question 5.
Starting from the origin, a body oscillates simple harmonically with an amplitude of 2m and a period of 2s.

1. What do you mean simple harmonic motion.
2. Draw the variation of displacement with time for the above motion.
3. After what time, will its kinetic energy be 75% of the total energy?

Answer:
1. The oscillatory motion is said to be simple harmonic motion if the displacement ‘x’ of the particle from the origin varies with time as

where
x(t) = displacement x as a function of time t
A = amplitude
ω = angular frequency
(ω t + Φ) = phase (time-dependent)
Φ = phase constant or initial phase

2.

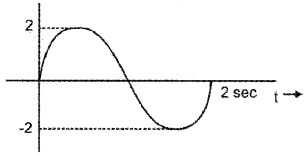
3. y = a sin ω t
ν = aω cos ωt
Kinetic energy,

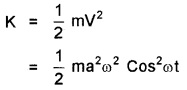
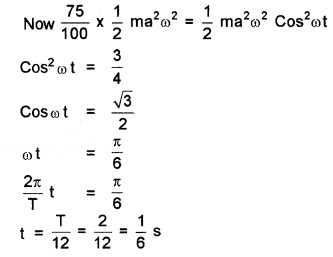
Question 6.
A body of mass 16 kg is oscillating on a spring of force constant 100 N/m.

1. What do you mean by spring constant?
2. Derive a general expression for the period of oscillating spring.

Answer:
1. Spring constant is the force required for unit extension.

2.

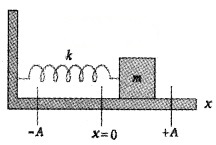
Consider a body of mass m attached to a massless spring of spring constant K. The other end of spring is connected to a rigid support as shown in figure. The body is placed on a frictionless horizontal surface.

If the body be displaced towards right through a small distance Y, a restoring force will be developed.

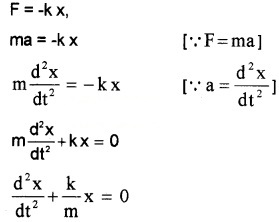
Comparing this equation with standard differential equation \(\frac{d^{2} x}{d t^{2}}\) + ω²x = 0
We get ω² = k/m

Question 7.
A particle execute simple harmonic motion according to the equation, x = 5sin \(\left(\frac{2 \pi}{3}\right) t\)

1. What is the period of the oscillation?
2. Write an expression for velocity and acceleration of the above particle.

Answer:
1. When x = 5sin\(\left(\frac{2 \pi}{3}\right) t\) with standard equation.
x = asin ω t we get

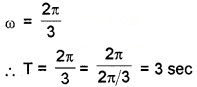
2. Velocity V = \(\frac{d}{d t}\) 5sin\(\left(\frac{2 \pi}{3}\right) t\)

Question 8.

1. Arrive the differential equation of SHM.
2. What do you mean by seconds pendulum.

Answer:
1. The force acting simple harmonic motion is proportional to the displacement and is always directed towards the centre of motion.

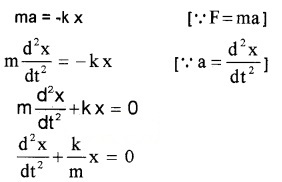
Comparing this equation with standard differential equation \(\frac{d^{2} x}{d t^{2}}\) + ω²x = 0,
We get ω² = k/m.

2. A pendulum having period 2 sec is called a seconds pendulum.

Question 9.
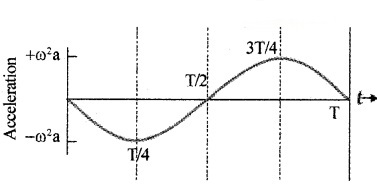
SHM is a type of motion in which both speed and acceleration change continuously.

1. Which of the following condition is sufficient for SHM?
   • a = ky,
   • a = ky
   • a = ky²
2. Draw a graph of SHM between
   • displacement-time
   • speed – time
   • acceleration -time

Answer:
1. a = ky

2. Variation of displacement Y with time t

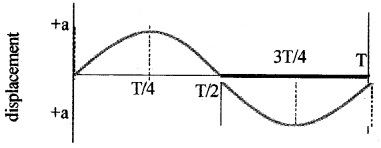
Variation of velocity Y with time t

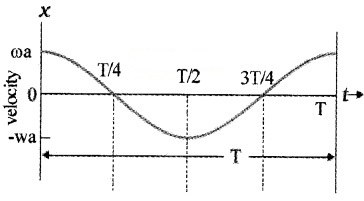
Variation of acceleration with time

Question 10.

1. Is oscillation of a mass suspended by a spring is simple harmonic?
2. Write a period of oscillation of the spring?
3. There are two springs, one delicate and another stout. For which spring, the frequency of oscillation will be more?
4. Two unequal springs of the same material are loaded with the same load, which one will have a large value of time period?

Answer:
1. Yes

2. T = \(2 \pi \sqrt{\frac{m}{k}}\)

3. When a stout spring loaded with mass ‘m’, the extension (l) produced is large.
∴ T is large, because T = \(2 \pi \sqrt{\frac{m}{k}}\),
T is small, i.e, frequency is large. Stout spring oscillate with larger frequency.

4. When a longer spring is locked with weight mg, the extension T is more
∴ T is large, because T = \(2 \pi \sqrt{\frac{l}{g}}\)
So longer spring will have a large value of period.

Question 11.
A simple pendulum consists of a metallic bob suspended from a long straight thread whose one
end is fixed to a rigid support.

1. What is the time period of second’s pendulum?
2. Derive an expression for period of simple pendulum.

Answer:
1. 2 sec

2.

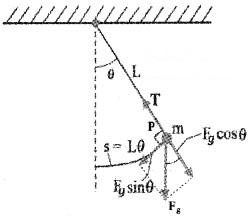
Consider a mass m suspended from one end of a string of length L fixed at the other end as shown in figure. Suppose P is the instantaneous position of the pendulum. At this instant its string makes an angle θ with the vertical.

The forces acting on the bob are (1) weight of bob F_g(mg) acting vertically downward. (2) Tension T in the string.

The gravitational force F_g can be divided into a radial component F_gCosθ and tangential component F_gSinθ. The tangential component F_gSinθ produces a restoring torque.
Restoring torque τ = – F_g sinθ . L
τ = – m_g sinθ . L _____(1)
-ve sign shown that the torque and angular displacement θ are oppositely directed. For rotational motion of bob,
τ = Iα ______(2)
Where I is moment of inertia about the point of suspension and α is angular acceleration. From eq (1) and eq (2).
Iα = – mgsinθ . L
If we assume that the displacement θ is small, sinθ ≈ θ
∴ Iα = -mgθ . L
Iα + mgθ L = 0

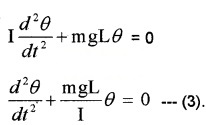
Comparing eq (3) with a standard differential equation


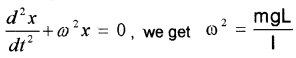
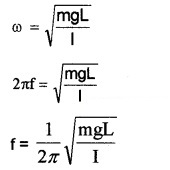
∴ period of simple pendulum,

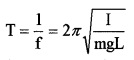
for simple pendulum, I = mL²
Substituting I = mL² we get

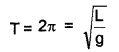
The above equation gives that T is independent of mass.

Plus One Physics Oscillations Five Mark Questions and Answers

Question 1.

1. Which of the following condition is sufficient for the simple harmonic motion?
   • a = ky
   • a = ky²
   • a = -ky
   • a = -ky²
     Where ‘a’ – acceleration, y – displacement
2. Prove that simple harmonic motion is the projection of uniform circular motion on any diameter of the circle.
3. Represent graphically the variations of potential energy, kinetic energy and total energy as a function of position ‘x’ for a linear harmonic oscillator. Explain the graph.

Answer:
1. a = -ky

2.

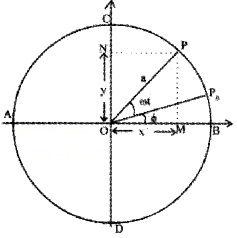
Consider a particle moving along the circumference of a circle of radius ‘a’ and centre O, with uniform angular velocity w. AB and CD are two mutually perpendicular diameters along X and Y axis. At time t = 0.

let the particle be at P₀ so that ∠P₀OB = Φ. After time ‘t’ second, let the particle reach P so that ∠POP₀ = ω t. N is the foot of the perpendicular drawn from P on the diameter CD.

Similarly M is the foot of the perpendicular drawn from P to the diameter AB. When the particle moves along the circumference of the circle, the foot of the perpendicular executes to and fro motion along the diameter CD or AB with O as the mean position.

From the right angle triangle O MP, we get
Cos (ωt + Φ) = \(\frac{O M}{O P}\)
∴ OM = OPcos(ωt + Φ)
X= a cos (ωt + Φ) _______(1)
Similarly, we get
Sin (ωt + Φ) = \(\frac{y}{a}\) (or)
Y = a sin (ωt + Φ) _______(2)
Equation (1) and (2) are similar to equations of S.H.M. The equation(1) and (2) shows that the projection of uniform circular motion on any diameter is S.H.M.

3. KE = PE
\(\frac{1}{2}\)mω²(a² – x²) = \(\frac{1}{2}\) = mω²x²
Solving we get, x = \(\frac{a}{\sqrt{2}}\)
where a is the amplitude of oscillation.

Question 2.
The spring has a scale that reads from zero to 30 kg. The length of the scale is 30cm.

1. Calculate the force constant K
2. If the period of oscillation is 1 sec. Calculate mass of the body attached to the spring.
3. If the spring is cut into two halves, What is the force constant of each half?

Answer:
1. 30 cm = 30kg
1 cm = \(\frac{30}{30}\) = 1kg
∴ Spring constant K = 1 kg/cm = 10N/cm =1000N/m.

2.

3. If spring of spring constant K is cut into half, spring constant of each half became, 2K

Plus One Physics Oscillations NCERT Questions and Answers

Question 1.
Which of the following examples represent periodic motion?
(a) A swimmer completing one (return) trip from one bank of a river to the other and back.
(b) A freely suspended bar magnet displaced from its N-S direction and released.
(c) A hydrogen molecule rotating about its centre of mass.
(d) An arrow released from a bow.
Answer:
(b) A freely suspended bar magnet displaced from its N-S direction and released and
(c) A hydrogen molecule rotating about its centre of mass

Question 2.
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7x
(b) a = 200x²
(c) a = 10x
(d) a = 100x²
Answer:
Only (c) ie. a = -10x represent SHM. This is because acceleration is proportional and opposite to displacement (x).

Question 3.
A spring having spring constant 1200Nm^-1 is mounted on a horizontal table as shown in the figure. A mass of 3 kg is attached to the free end of the spring. The mass is pulled sideways to a distance of 2.0cm and released.

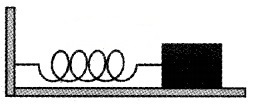
Determine

1. the frequency of oscillations,
2. maximum acceleration of the mass and
3. the maximum speed of the mass.

Answer:
k = 1200Nm^-1, m = 3kg, a = 2.0cm = 2 × 10^-2m
1.

2. Maximum acceleration = ω² a = \(\frac{k}{m}\)a

3. Maximum speed = aω = a\(\sqrt{\frac{K}{m}}\)

Question 4.
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0m. If the position moves with simple harmonic motion with an angular frequency of 200 rev/min, what is its maximum speed?
Answer:
a = \(\frac{1}{2}\)m, ω = 200 rev/min
U_max = aω = \(\frac{1}{2}\) × 200m/min = 100 m/min.

Question 5.
A circular disc of mass 10kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15cm. Determine the torsional spring constant of the wire. (Torsional spring constant α is defined by the relation J = -αθ, where J is the restoring couple and θ the angle of twist).
Answer:

Plus One Physics Chapter Wise Questions and Answers