Kerala Plus One Physics Chapter Wise Previous Questions Chapter 6 Work, Energy and Power
Question 1.
Collision between two particles need not be the physical contact of two particles as in the case of scattering of the α – particle by a nucleus. (MARCH-2010)
a) What is the quantity that remains conserved in all types of collisions?
b) Suppose an electron and a proton are projected with equal kinetic energy, what will be the ratio of their linear momentums if the proton is 1830 times heavier than an electron?
c) The bob of a pendulum released from 30° to the
vertical hits on another bob of equal mass at rest. How high does the first bob rise afterthe collision? (Assume that the collision is elastic and the size of the bobs are negligible.)
Answer:
a) Momentum is always conserved
b) Kinetic energy of electron
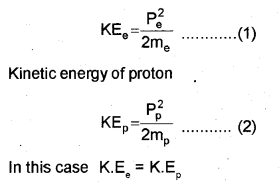
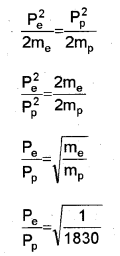
This is an elastic collision. Hence the kinetic energy of first body is transferred to second body. If h is the height of first body, then second body rises to the same height h.
Question 2.
Work is related to force and displacement over which it acts. (MAY-2010)
a) A man tries to pull a rigid wall for a long time but
fails to displace it. What is the external work done by him?
b) Suggest two conditions for the work done by a force to be zero.
c) A body of mass 1 kg travels in a straight line with a velocity kx3/2 where k = 5 SI units.
Calculate the work done by the net force to displacefromx = 0 to x = 2m.
Answer:
a) Work done = Force x displacement In this case displacement is zero. Hence work done=0
b)i) θ = 90° (angle between Force and displacement is 90°)
ii) Displacement = 0
c) Work done = Change in kinetic energy
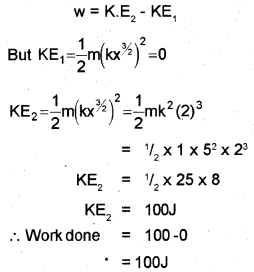
Question 3.
A ball moves along a circle under the influence of centripetal force. (MAY-2010)
a) What is the work done by the centripetal force on the ball ?
b) An arrow shot from a bow has kinetic energy.
How does it get this kinetic energy ?
c) Show that the total mechanical energy of a freely falling body is conserved.
Answer:
w = Fdcosθ
for circular motion the angle between F and d is 90°.
w = Fdcos90°
= 0
b) The potential energy stored in spring is transferred to arrow.
c)
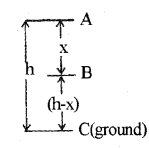
Consider a body of mass ‘m’ at a height h from the ground.
Total energy at the point A
Potential energy at A,
PE = mgh
kinetic energy K.E = 1/2 mv² = 0
(since the body at rest, v = 0).
Total mechanical energy = PE + KE
= mgh + 0 = mgh
Total energy at the point B
The body travels a distance x when it reaches B. The velocity at B, can be found using the formula.
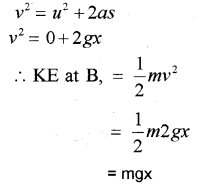
P.E at B = mg(h – x)
Total energy = PE + KE
= mg(h – x) + mgh
= mgh
Total energy at C
Velocity at C can be found using the formula
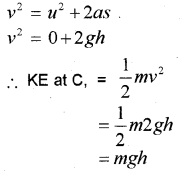
Question 4.
When brakes are applied on a moving vehicle, it stops aftertravelling a distance. This distance is called stop-ping distance. (MARCH-2011)
a) Write an expression of stopping distance in terms of initial velocity (u) and retardation (a).
b) If the initial speed is doubled keeping the retardation same, by how much will the stopping distance change ?
Answer:
a) When vehicle comes to rest, v = 0, a = – a
substituting these values in v²= u² + 2as, we get 0 = u² – 2as

ie the stopping distance becomes 4 times the .original distance.
Question 5.
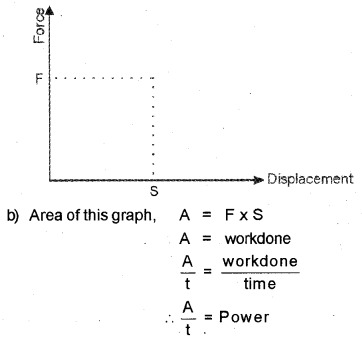
Ramesh lifts a body of mass ‘m’ to a height ‘h’ near the surface of the earth in a time ‘t’. (MARCH-2011)
a) Drawthe force-displacement graph.
b) If ‘A’ is the area of the graph, what quantity does (A/T) indicate?
Answer:
a)
Question 6.
According to the work-energy theorem, work done by a force on a body is equal to change in its kinetic energy. (MARCH-2011)
A lorry and a car moving with the same kinetic energy are stopped by applying brakes which provides the same retardation. Which of them will come to a rest in a shorter distance? Explain.
Answer:
Workdone = Change in kinetic energy
FS = KE


Question 7.
A force is required to do work. The work done by a force is the product of displacement and the compo-nent of force in the direction of displacement. Prove this statement. (MAY-2011)
Answer:
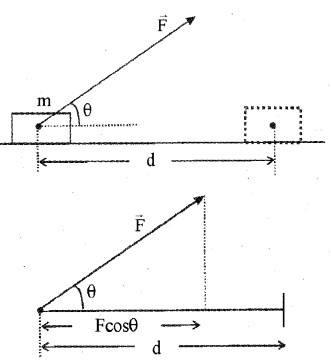
Consider a constant force \(\overrightarrow{\mathrm{F}}\) acting on an object of mass m. The object undergoes a displacement d in the positive x direction as shown in the figure. The projection of \(\overrightarrow{\mathrm{F}}\) on d is Fcosθ.
Hence work done
w = Fcosθ.d
w = Fdcosθ
w = \(\overrightarrow{\mathrm{F}}\)\(\overrightarrow{\mathrm{d}}\)
Question 8.
Consider a body falling freely through the atmosphere. Neglecting the air resistance prove that the total mechanical energy of the body remains con, stant throughout the fall. (MARCH-2011)
Answer:

Consider a body of mass ‘m’ at a height h from the ground.
Total energy at the point A
Potential energy at A,
PE = mgh
kinetic energy K.E = 1/2 mv² = 0
(since the body at rest, v = 0).
Total mechanical energy = PE + KE
= mgh + 0 = mgh
Total energy at the point B
The body travels a distance x when it reaches B. The velocity at B, can be found using the formula.
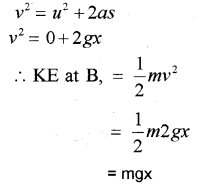
P.E at B = mg(h – x)
Total energy = PE + KE
= mg(h – x) + mgh
= mgh
Total energy at C
Velocity at C can be found using the formula
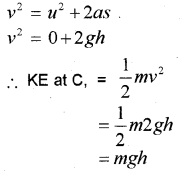
Question 9.
Say True or False : (MAY-2011)
The total energy of a body is equal to the work it can do in being brought to rest.
Answer:
False
Question 10.
Work is required to lift a body through a height from the ground. (MARCH-2012)
a) Calculate the work done in lifting a body of mass 10 kg to a height of 10m above the ground.
b) State and prove the law of conservation of energy of a freely falling body.
c) Draw the variation of KE and PE with the height of the body.
Answer:
a) Work done = Force x displacement
W = mg x h
= 10 x 9.8 x 10 W
= 980J
b)

Consider a body of mass ‘m’ at a height h from the ground.
Total energy at the point A
Potential energy at A,
PE = mgh
kinetic energy K.E = 1/2 mv² = 0
(since the body at rest, v = 0).
Total mechanical energy = PE + KE
= mgh + 0 = mgh
Total energy at the point B
The body travels a distance x when it reaches B. The velocity at B, can be found using the formula.
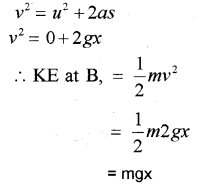
P.E at B = mg(h – x)
Total energy = PE + KE
= mg(h – x) + mgh
= mgh
Total energy at C
Velocity at C can be found using the formula
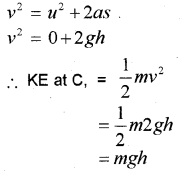
c)
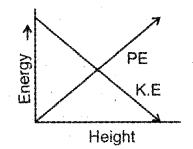
Question 11.
a) State and prove the law of conservation of energy for a freely falling body. (MAY-2012)
b) Draw graphically the variation of kinetic energy and potential energy with the height of the body in the above case.
Answer:
a)

Consider a body of mass ‘m’ at a height h from the ground.
Total energy at the point A
Potential energy at A,
PE = mgh
kinetic energy K.E = 1/2 mv² = 0
(since the body at rest, v = 0).
Total mechanical energy = PE + KE
= mgh + 0 = mgh
Total energy at the point B
The body travels a distance x when it reaches B. The velocity at B, can be found using the formula.
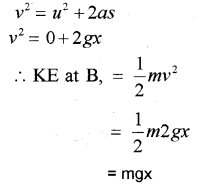
P.E at B = mg(h – x)
Total energy = PE + KE
= mg(h – x) + mgh
= mgh
Total energy at C
Velocity at C can be found using the formula
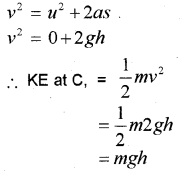
b)

Question 12.
Fill in the blanks. (MARCH-2013)
| a) ………………… | \(\overrightarrow{\mathrm{F}}\).\(\overrightarrow{\mathrm{S}}\) | scalar quantity |
| b) mass, m | momentum, p | KE =……….. |
| c) ….collision | momentum conserved | energy conserved |
| d) unit of power | …………………. | 746 watt |
| e) Body of mass, m | at a height, h | PE =……… |
| f) Power, P | P =……………. | scalarproduct |
Answer:
| a) work done | \(\overrightarrow{\mathrm{F}}\).\(\overrightarrow{\mathrm{S}}\) | scalar quantity |
| b) mass, m | momentum, p | KE = \(\frac { p² }{ 2m }\) |
| c) elastic collision | momentum conserved | energy conserved |
| d) unit of power | I Hp | 746 watt |
| e) Body of mass, m | at a height, h | PE = mgh |
| f) Power, P | P =\(\overrightarrow{\mathrm{F}}\).\(\overrightarrow{\mathrm{V}}\) | scalar product |
Question 13.
State and explain the work done in the following situations: (MARCH-2013)
i) A person carrying a heavy load walks on a level road.
ii) A man spending his energy by pushing on a concrete wall.
A constant force of 200N displaces a body through 5 m in the direction of the force. Find the work done on the body.
Answer:
i) Work done is zero in vertical direction. Because there is no displacement along vertical direction.
ii) In this case there is no displacement hence work done is zero.
Work done = FdCosθ
= 200 x 5 x Cos O
w = 1000J
Question 14.
A car is moving with a constant speed on a straight line (MAY-2013)
a) What is the net work done by the external force on the car?
b) State work energy theorem.
c) A bullet of mass 10 g and velocity 800 m/s is
passed through a mud wall of thickness 1 m. Its velocity reduces to 100 m/s. Find the average resistance offered by the mud wall.
Answer:
a) When car is moving with constant speed, Work done = Ffriction x displacement, if there is no friction work done = 0
b) The change in kinetic energy of a particle is equal to the work done on it by the net force.
c) Work done = Change in KE
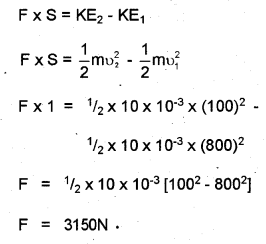
Question 15.
From the table given below: (MARCH-2014)
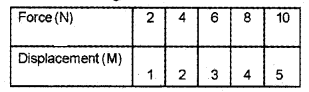
a) Drawthe force-displacement graph.
b) How can you find the work done from the above graph?
c) Suggest any two situations in which the work done by a force is zero.
d) A body is pushed with a force of 3N for 2s along a frictionless track. The graph shows the velocity of the body against time.
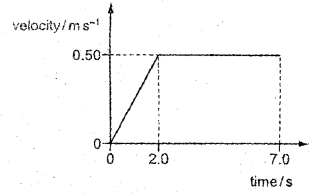
How much work is done by the force?
Answer:
a)
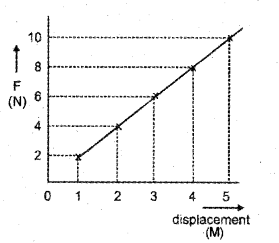
b) Area of force displacement graph gives work done.
c) 1) A body is revolving around a circle with uniform speed.
2) A man is walking along a level road carrying a load on his head. In this case there is no work , done along vertical direction.
d) This work is done on a frictionless track. Hence need not find work done when body moves with constant velocity.
(But there will be work done when it moves with acceleration.)
From graph, acceleration
a = \(\frac { 0.5 – 0 }{ 2 }\)
a = 0.25 m/s²
Displacement in a time t = 2
S = ut + 1/2 at²
S = 0 + 1/2 x 0.25 x 2²
S = 2 x 0.25
S = 0.5 m
Work done = Force x displacement
= 3 x 0.5
W = 1.5 J
Question 16.
Below figure represents two point masses, m1 and m2 approaching each other with speeds u1 and u2. Let them undergo one-dimensional collision and retrieve each other with velocities v1 and v2. (MAY-2014)
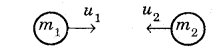
Show that (u1 – u2) = – (v1 – v2), ie, after collision, their relative velocities are equal.
Answer:

Question 17.
The scalar product of force and displacement gives work. It can be negative, zero or positive. (MAY-2014)
a) The work done in sliding a load is with respect to frictional force, (zero, positive, nega-tive, )
b) State and prove the work energy theorem for con-stant force.
A pump on the ground floor of a building can pump water to fill a tank of volume 30m3 in 15 minutes. If the tank is 40m above the ground and the efficiency of the pump is 30%, how much electric power is consumed by the pump?
OR
Several games such as billiards, marbles or carrom involve collisions.
a) When two objects collide, after collision they could move together, the collision is
(elastic, completely elastic, inelastic, completely inelastic)
b) Show that in a perfectly elastic collision in one dimension, relative velocity after collision is equal to relative velocity before collision.
c) A ball at rest is dropped from a height of 12m. It loses 25% of its kinetic energy on striking the ground. Find the height to which it bounces.
Answer:
a) negative
b) Statement
The change in kinetic energy of a particle is equal to the work done on it by the net force.
Proof
We know v² = u² + 2as
v² – u² = 2as
Multiplying both sides with m/2; we get

OR
a) Completely elastic
b) Refer Q.No. 1, Say 2014
c) When a body strikes at ground, the total Kinetic energy KE1 = mgh1
25% of KE is lost.
Remaining energy = 75%
= 0.75 mgh1
When it rebounds to a height h2, we can write
mgh2 = 0.75 mgh1
h2 = 0.75h1
= 0.75 x 12
= 9 m
Question 18.
The figure shows a body of mass m placed at a height h. A, B and C are the three points on the trajectory of this body. (MAY-2015)
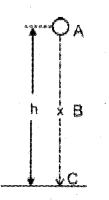
a) Which is the type of energy possessed by this body at a height h?
b) Prove that total mechanical energy is conserved at B and C.
Answer:
a) Potential energy
b)

Consider a body of mass ‘m’ at a height h from the ground.
Total energy at the point A
Potential energy at A,
PE = mgh
kinetic energy K.E = 1/2 mv² = 0
(since the body at rest, v = 0).
Total mechanical energy = PE + KE
= mgh + 0 = mgh
Total energy at the point B
The body travels a distance x when it reaches B. The velocity at B, can be found using the formula.
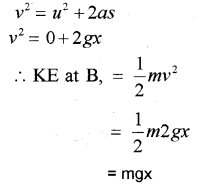
P.E at B = mg(h – x)
Total energy = PE + KE
= mg(h – x) + mgh
= mgh
Total energy at C
Velocity at C can be found using the formula
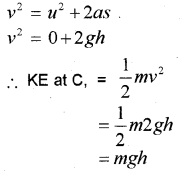
Question 19.
Force is required to lift a body from the ground to a height h and work is measured as the product of force and magnitude of displacement. (MARCH-2016)
a) Name the energy possessed by the body at maxi-mum height. Write an equation for it.
b) A man of mass 60 kg carries a stone of mass 20 kg to the top of a multistoreyed building of height 50 m. Calculate the total energy spent by him? (g= 9.8 m/s²)
Answer:
a) Potential energy, PE=mgh
b) m= 80 kg, g = 9.8 m/s², h= 50 m
Total energy = mgh = 80 x 9.8 x 50=39200J
Question 20.
a) State work energy theorem. (MAY-2016)
b) Show that the potential energy of a body is . completely converted into kinetic energy during its free fall under the gravity.
c) A man carefully brings down a glass sheet from a height 2 m to the ground. The work done by him is
i) negative
ii) zero
iii) positive
iv) unpredictable
Answer:
“The change in kinetic energy of a particle is equal to the work done on it by the net force”.
b)
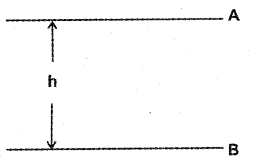
Consider a body of mass m be dropped from height ‘h’to the ground.

Hence PE is completed converted KE for a free fall body.
c) i) negative
Question 21.
Energy of a body is defined as its capacity of doing work. (MARCH-2017)
a) The energy possessed by a body by virtue of motion is known as ………….
b) A body of mass 5 kg initially at rest is subjected to a horizontal force of 20N. What is the kinetic energy acquired by the body at the end of 10 s?
c) State whether the following statement is TRUE or FALSE.
Answer:
a) Kinetic energy
b)

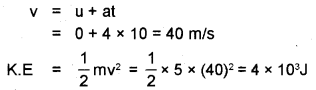
c) true