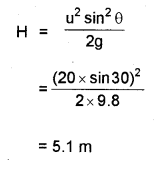Plus One Physics Chapter Wise Previous Questions Chapter 4 Motion in a Plane

Kerala Plus One Physics Chapter Wise Previous Questions Chapter 4 Motion in a Plane

Question 1.
Ramesh observes the motion of an insect in a circle. He finds that it travels 6 revolutions in an anti-clockwise direction for a time of 31.4 sec. (MARCH – 2010)
a) Find the angular velocity of the insect.
b) If the insect travels 4 revolutions in the clockwise direction for a time of 8.6 sec, what will be the angularspeed averaged overthe total time?
c) Obtain the expression for centripetal acceleration
(a) in terms of angularspeed (ω).
Answer:


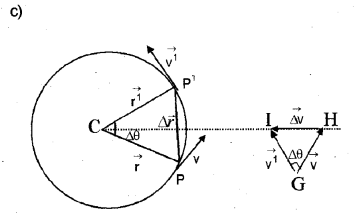
The velocity vectors \(\overrightarrow{\mathrm{v}} \text { and } \overrightarrow{\mathrm{v}^{1}}\) are always perendicular to \(\overrightarrow{\mathrm{r}} \text { and } \overrightarrow{\mathrm{r}^{1}}\) . Therefore the triangle CPP₁ (formed by the position vectors \(\overrightarrow{\mathrm{r}} \text { and } \overrightarrow{\mathrm{r}^{1}}\)) and the triangle GHI (formed by velocity vectors \(\overrightarrow{\mathrm{v}} \text { and } \overrightarrow{\mathrm{v}^{1}}\)) are similar triangles. Therefore the ratio of base length to side-length for one of the triangle is equal to the other triangle.

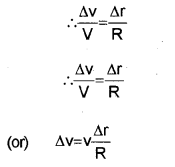
dividing the above equation with ∆t, we get

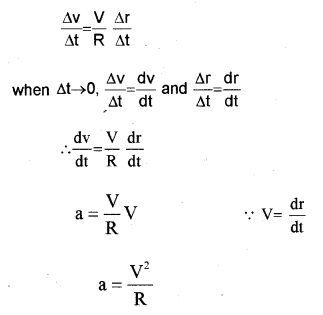
The acceleration is directed towards the centre of the circle and is called centripetal acceleration.
a₀ = v²/R
but V = Rω
substituting we get
a_c = rω²

Question 2.
Imagine yourself in a rain, steadily falling vertically with a speed of 2ms^{– 1}. (MARCH – 2010)
a) If you start moving with 1 ms_-1 due east, in which direction should you hold the umbrella to protect yourself from the rain?
b) On a sunny day at 12 noon, you hold the umbrella vertically. If you run at certain speed, do you need to incline the umbrella? Justify your answer.
Answer:
a)

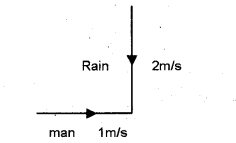
To find the direction of umbrella, reverse the velocity of man and add to velocity of rain using vector law.

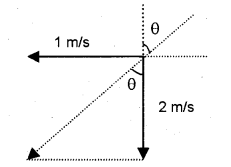
From the above triangle tanθ = 1/2 = 0.5 (or) θ = tan^{– 1} 0.5 = 26⁰ 34^{– 1}
Umbrella should hold at an angle 26⁰ 34^{– 1} from the vertical.
b) The speed of light is very large.
Hence the resultant vector will be in the direction of incident light.Hence we should hold umbrella at an angle 90⁰.

Question 3.
A ball is thrown horizontally from the top of a tower with a velocity of 40 ms^{– 1}. (MARCH – 2010)
Take g = 10 ms².
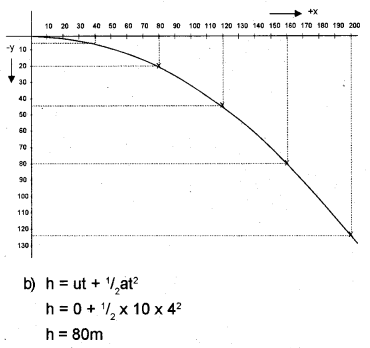
a) Find the horizontal and vertical displacement after 1,2, 3,4, 5 seconds, then plot the path of motion of the ball.
b) If the ball reaches the ground in 4 seconds, find the height of the tower.
Answer:
a) 1 second
Horizontal distance, x = 40 x 1 = 40m
Vertical distance, y = ut + 1/2 at²
= 0 + 1/2 x 10 x 1²
= 5m
2 second
Horizontal distance x = 40 x 2 = 80m
Vertical distance y = 1/2 x 10 x 2² = 20m
3 second
Horizontal distance x = 40 x 3 = 120m
Vertical distance y = 1/2 x 10 x 3² = 45m
4 second
Horizontal distance x = 40 x 4 = 160m
Vertical distance y = 1/2 x 10 x 4² = 80m
5 second
Horizontal distance x = 40 x 5 = 200m
Vertical distance y = 1/2 x 10 x 5² = 125m

Question 4.
A stone is thrown up with a velocity u which makes an angle θ with the horizontal. (MAY – 2010)
a) What are the magnitudes of the horizontal and vertical components of velocity ?
b) How do these components change with time?
c) After T second what will be the magnitude and direction of the resultant velocity ?
Answer:
a) ucosθ and usinθ
b) ucosθ remains constant.
usinθ decreases and becomes zero.
c) Vertical velocity aftertimet,

Question 5.
Motion along a plane is called two dimensional motion. A body moving in two dimensions is found to have an acceleration in one dimension. (MARCH – 2011)
a) Identify the motion.
b) A ball thrown by a player reaches another player in 2s. What is the maximum height attained by the ball above the point of projection ?
(Take g = 10 ms^-2).
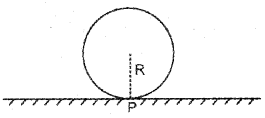
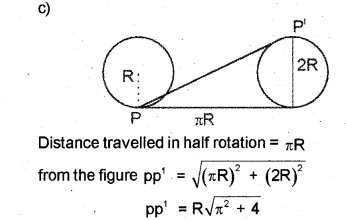
c) In the figure, the point P on a wheel of radius R is
in contact with the ground. What is the displacement of the point, when the wheel rolls a half revolution?

Answer:
b)
a) Projecticle motion.

Question 6.
A food packet is dropped from a plane flying horizontally. (MAY – 2011)
a) Sketch the path of the falling food packet.
b) If the time taken by the packet to reach the earth’s surface is ‘6’ seconds, calculate the height from which the packet is dropped. (Take g = 10m/s²)
Answer:
a)

b) Initial velocity in downward direction u = 0, a = 10 and t = 6 see. Substituting these values in this equation.
S = ut + 1/2 at²
S = 0 + 1/2 x 10 x 6²
S = 180 m
height = 180 m

Question 7.
A parallelogram law helps to find the magnitude and direction of the resultant of two forces: (MARCH – 2012)
a) State the law.
b) If the magnitude of two vectors and their resultant are the same, what is the angle between the two vectors?
c) Determine the value of \((\overrightarrow{\mathrm{A}}-\overrightarrow{\mathrm{B}}) \times(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}})\)
Answer:
a) Parallelogram law of vector addition
This law states that if two vectors acting at a point can be represented in magnitude and direction by the two adjacent sides of a parallelogram, then the diagonal of the parallelogram through that point represents the resultant vector.
b) R = \(\sqrt{A^{2}+B^{2}+2 A B \cos \theta}\)
Here R = F, A = F and B = F
F = \(\sqrt{F^{2}+F^{2}+2 F^{2} \cos \theta}\)
F² = F²+ F²+ 2F²Cos θ
F² = 2F² + 2F² Cos θ
F² – 2F² = 2F² Cos θ
F² = 2F² Cos θ
-1/2 = Cos θ
θ = 120°
c)

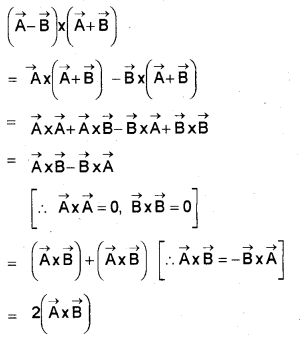
Question 8.
A boy throws a cricket ball with a velocity u at an angle θ with the horizontal. (MARCH – 2012)
a) Name the path followed by the ball.
b) At the highest point, what are the vertical and horizontal components of velocity?
c) Derive an expression for the maximum height reached by the ball.
d)

If θ₁ = 30°, then what is the value of θ₂
Answer:
a) parabola
b) Vertical velocity becomes zero at highest point, ie vertical velocity at heighest point, v_y = 0
Horizontal velocity does not change with height, ie horizontal velocity v_x = u Cos θ.
c) Vertical height of body is decided by vertical com-ponent of velocity (u sinθ). The vertical displace-ment of projectile can be found using the formula
v² = u² + 2as
When we substitute v = 0, a = – g,s = H and u = usinθ, we get
0 = (usinθ)² + 2 – g x H
2gH = u²sin²θ
H = \(\frac { u²sin²θ }{ 2g }\)
d) There are 2 angles of projection θ₁ and θ₂ giving the same range R.
The relation between θ₁ andθ₂
θ₂= 90 – θ₁
If θ₁ = 30°,
Then θ₂= 90 – 30 .
θ₂ = 60°

Question 9.
A car is moving along the circumference of a circle of radius r. (MAY – 2012)
a) What is the distance travelled in one revolution?
b) What is its displacement in one revolution?
c) What does the speedometer of the car measure?
d) Can a body have acceleration without velocity.Explain.
Answer:
a) distance travelled = 2πr
b) displacement = 0
c) Instantaneous speed
d) Yes. When a body is projected vertically up, its velocity becomes zero and acceleratoin is 9.8 m/s² at maximum height.

Question 10.
a) Find whether the given vectors \(2 \hat{i}+3 \hat{j}+4 \hat{k}\) and \(4 \hat{i}+6 \hat{j}+8 \hat{k}\) are parallel or not. (MAY – 2012)
b) What are orthogonal unit vectors?
c) What is a zero vector? Give its significance in Physics with an example.
Answer:
a)

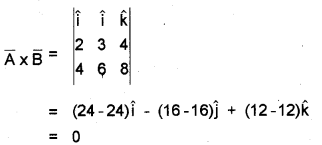
\(\bar{A} \times \bar{B}=0\), which means that angle between \(\overline{\mathrm{A}}\) and \(\overline{\mathrm{B}}\) is 0°.
b) \(\hat{\mathbf{i}}\), \(\hat{\mathbf{j}}\), and \(\hat{\mathbf{k}}\) are orthoganal unit vectors.
c) A vector having zero magnitude is called a zero vector.
Since magnitude is zero, we don’t have to specify its direction.
Example
Suppose that an object which is at p at time t moves to p’ and then comes back to p. In this case displacement is null vector.

Question 11.
a) Obtain expression for Time of flight for a projectile motion. (MAY – 2012)
b) What is the angle of projection for maximum horizontal range?
c) The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that the ball thrown with a speed of 40 m/s can go without hitting the ceiling of the hall?
Answer:
a) The time taken by the projectile to cover the horizontal range is called the time of flight.
Time of flight of projectile is decided by usinθ. The time of flight can be found using the formula
s = ut + 1/2 at²
Taking vertical displacement s=0, a = – g and initial vertical velocity = usinθ, we get
0 = usinθt – 1/2gt²
1/2 gt² = usinθt
t = \(\frac { 2usinθ }{ g }\)
b) We get maximum horizontal range at θ = 45
c) Here H = 25 m, u = 40 m/s
Suppose that the ball is thrown at an angle θ with the horizontal

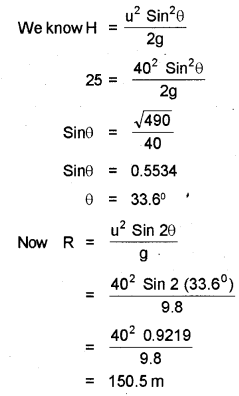
Question 12.
An athlete jumps at an angle of 30° with a maximum speed of 9.4 m/s.  (MARCH – 2013)
a) What is the shape of the path followed by the athlete in the jump?
b) Obtain an expression to calculate the horizontal range covered by the athlete.
c) Find the range covered by him in the above jump. Suggest the angle by which the athlete can attain the maximum range.
Answer:
a) Parabolic path
b) If we neglect the air resistance, the horizontal velocity (ucosθ) of projectile will be a constant. Hence the horizontal distance (R) can be found as

Question 13.
A stone is thrown upward from a moving train, (MAY – 2013)
a) Name the path followed by the stone.
b) A particle is projected with a velocity ‘u’ in the direction making an angle 9 with the horizontal.
Find:
1) Time of flight
2) Maximum height
c) A man can jump on moon six times as high as on earth. Why?
Answer:
a) Parabola
b) 1) The time taken by the projectile to coverthe hori-zontal range is called the time of flight.
Time of flight of projectile is decided by usin9. The time of flight can be found using the formula
s = ut + 1/2 at²
Taking vertical displacement s=0, a = – g and initial vertical velocity = usinθ, we get
0 = usinθt – 1/2gt²
1/2 gt² = usinθt
t = \(\frac { 2usinθ }{ g }\)
2) Vertical height of body is decided by vertical component of velocity (u sinθ). The vertical displacement of projectile can be found using the formula
v² = u² + 2as
When we substitute v = 0, a = – g,s = H and u = usinθ, we get
0 = (usinθ)² + 2 – g x H
2gH = u²sin²θ
H = \(\frac { u²sin²θ }{ 2g }\)
The value of g on the moon is one sixth of that on earth. Hence a man can jump on moon six times as high as on earth.

Question 14.
A and B are two objects moving with velocities\(\overline{\mathrm{V}_{\mathrm{A}}}\) and \(\overline{\mathrm{V}_{\mathrm{B}}}\) . (MARCH – 2014)
a) What is the velocity of A relative toB?
b) Rain is falling vertically with a speed of 35 m/s. A woman rides a bicycle with a speed of 12 m/s in the east to west direction. What is the direction in which she should hold her umbrella?
c) Assertion: The range of a projectile remains the same for the angle of projections 30° and 60°. Reason: The range does not depend on the angle of projection.
Choose the correct answer:
A : Both assertion and reason are correct.
B : Both assertion and reason are wrong.
C Assertion is correct, but reason is wrong.
D Assertion is wrong, but reason is correct.
Answer:

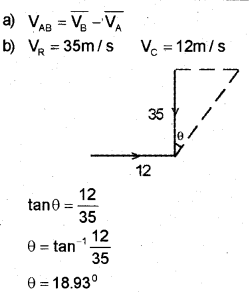
The boy should hold his umbrella at an angle of 18.93° from vertical.
c) C

Question 15.
Projectile is a particle which is projected into the air with an initial velocity against gravity. (MAY – 2014)
a) What is the angle of projection for maximum horizontal range?
b) Draw the trajectory of a projectile.
c) Obtain the expression for time of flight.
Answer:
a) θ = 45°
b)

c) The time taken by the projectile to coverthe hori-zontal range is called the time of flight.
Time of flight of projectile is decided by usin9. The time of flight can be found using the formula
s = ut + 1/2 at²
Taking vertical displacement s=0, a = – g and initial vertical velocity = usinθ, we get
0 = usinθt – 1/2gt²
1/2 gt² = usinθt
t = \(\frac { 2usinθ }{ g }\)

Question 16.
Uniform circular motion is a special case of two-dimensional motion having centripetal acceleration. (MAY – 2014)
a) Define centripetal acceleration.
b) Can a body have acceleration with constant speed? Explain.
c) Express angular velocity in terms of angular displacement.
Answer:
a) In circular motion, the direction of acceleration is towards the centre. This acceleration is called centripetal acceleration.
b)Yes. Eventhough magnitude of velocity (speed) is constant, change in direction of velocity produces acceleration.
c) ω = \(\frac { dθ }{ dt }\)

Question 17.
A stone is thrown with the help of a sling with initial velocity v0 at an angle 0 from the horizontal. (MARCH – 2015)

a) Working of a sling is based on law of vector addition.
b) With the help of a vector diagram.state this law.
c) Derive the expression for the maximum height reached by the stone.
Answer:
a) Parallelogram
b) Parallelogram law of vector addition
This law states that if two vectors acting at a point can be represented in magnitude and direction by the two adjacent sides of a parallelogram, then the diagonal of the parallelogram through that point represents the resultant vector.
c) Vertical height of body is decided by vertical com-ponent of velocity (u sinθ). The vertical displace-ment of projectile can be found using the formula
v² = u² + 2as
When we substitute v = 0, a = – g,s = H and u = usinθ, we get
0 = (usinθ)² + 2 – g x H
2gH = u²sin²θ
H = \(\frac { u²sin²θ }{ 2g }\)

Question 18.
A body is projected into air at an angle 0 with the horizontal. (MAY – 2015)
a) What is the trajectory followed by this projectile?
i) Ellipse
ii) Parabola
iii) Straight line
iv) Circle
b) Give a mathematical proof for your answer.
c) Trajectory of a body in a projectile motion is given by y = \(y=x-\frac{x^{2}}{80}\) and y are in meters. Find maximum height of this projectile.
Answer:
a) ii, Parabola
b) The vertical displacement of projectile at any time t, can be found using the formula.
s = ut + 1/2 at²
y = usinθt – 1/2gt²
But we know horizontal displacement,

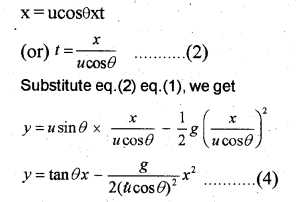
In this equation g, θ and u are constants. Hence eq.(4) can be written in the form
y = ax + bx²
where a and b are constants. This is the equation of parabola, ie. the path of the projectile is a parabola.
c) The standard equation for parabola is

Question 19.
When a body is projected into air with certain initial velocity making an angle with the horizontal, it will travel in a parabolic path. (MARCH – 2016)
a) What are the vertical and horizontal components of velocity?
b) With a diagram, derive an expression for:
i) Maximum height
ii) Time of flight
c) A ball is dropped through the window of a train travelling with high velocity, to a man standing nearthe track. The ball….
i) falls down vertically
ii) moves straight horizontally
iii) follows an elliptical path
iv) follows an parabolic path
Answer:
a) u cosθ and u sinθ
b) Vertical height of body is decided by vertical component of velocity (u sinθ). The vertical displacement of projectile can be found using the formula
v² = u² + 2as
When we substitute v = 0, a = – g,s = H and u = u sinθ, we get
0 = (usinθ)² + 2 – g x H
2gH = u²sin²θ
H = \(\frac { u²sin²θ }{ 2g }\)
ii) The time taken by the projectile to cover the horizontal range is called the time of flight.
Time of flight of projectile is decided by u sinθ. The time of flight can be found using the formula
s = ut + 1/2 at²
Taking vertical displacement s=0, a = – g and initial vertical velocity = u sinθ, we get
0 = u sinθt – 1/2gt²
1/2 gt² = u sinθt
t = \(\frac { 2usinθ }{ g }\)
c) iv) follows an parabolic path

Question 20.
a) Identify the scalar quantity from the following alternatives. (MAY – 2016)
i) Momentum
ii) Work
iii) Torque
iv) Acceleration
b) A man throws a stone up into air at an angle ‘θ’ with the horizontal. Draw the path of the projectile and mark directions of velocity and acceleration at the highest position.
c) Derive an expression for the maximum height reached by the stone.
Answer:
a) ii) work
b)

c) The time taken by the projectile to cover the horizontal range is called the time of flight.
Time of flight of projectile is decided by u sinθ. The time of flight can be found using the formula
s = ut + 1/2 at²
Taking vertical displacement s=0, a = – g and initial vertical velocity = u sinθ, we get
0 = u sinθt – 1/2gt²
1/2 gt² = u sinθt
t = \(\frac { 2usinθ }{ g }\)

Question 21.
Observe the following diagram. (MAY – 2016)

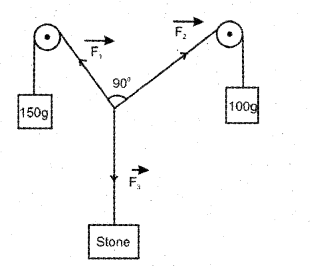
a) The forces \(\vec{F}_{1}\), \(\vec{F}_{2}\) and\(\vec{F}_{3}\) are together called ………….
b) Calculate the mass of the stone using the parallelogram law of vector addition.
Answer:
a) Concurrent froces
b) F₁ = 150 x g
F₂ = 100 x g and θ = 30°
F₃ = \(\sqrt{F_{1}^{2}+F_{2}^{2}+2 F_{1} F_{2} \cos \theta}\) .
F₃ = \sqrt{(150)^{2}+(100)^{2}+2 \times 150 \times 100 \cos 30^{\circ}}
F₃ = 241.82 g

Question 22.
a) Choose the correct statement / statements related to uniform circular motion. (MARCH – 2017)
i) The acceleration in uniform circular motion is tangential to the circle.
ii) The acceleration in uniform circular motion is directed radially inwards.
iii) The velocity in uniform circular motion has constant magnitude.
iv) The velocity in uniform circular motion is directed radially inwards.
b) A particle is projected up into air from a point with a speed of 20 m/s at an angle of projection 30°. What is the maximum height reached by it?
Answer:
a) ii) The acceleration in uniform circular motion is directed radially inwards.
iii) The velocity in uniform circular motion has constant magnitude.
b) u = 20 m/s, θ = 30°

Plus One Physics Chapter Wise Previous Questions