Kerala Plus One Physics Chapter Wise Previous Questions Chapter 3 Motion in a Straight Line
Question 1.
If ‘v’ is the velocity and ‘a’ is the acceleration, give an example of a physical situation for each of the following cases.(MARCH-2010)
a) v ≠ 0, a = 0
b) v = 0, a ≠ 0
c) v > 0, a <0
d) v < 0, a > 0
Answer:
a) A ball moving with uniform velocity.
b) A ball thrown upto reach highest point.
c) A ball moving upward (or) retarded motion while object is moving in the positive x – direction.
d) A ball moving down from a height
Question 2.
a) The figure shows the position time graph of a body moving along a straight line. (MARCH-2011)

i) Draw the velocity-time graph of the body.
ii) From the graph, find the displacement in 20 seconds.
b) From the velocity-time graph of a body moving with uniform acceleration, deduce the velocity-time relation and the velocity displacement relation.
Answer:
i) Slope of displacement-time graph gives velocity.

When we draw velocity – time graph, we get a graph as shown in the figure.
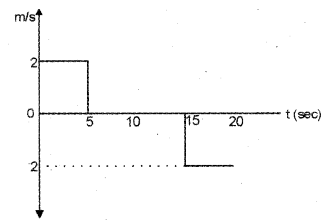
ii) Area under velocity – time graph gives displacement.
Area A = 2 x 5 + 2 x 5
A = 0
displacement = 0
b) Consider a body moving with uniform acceleration ‘a’. Let u be the initial velocity at a time t = 0 and v be the final velocity at time t. The velocity time graph of this body is given below.
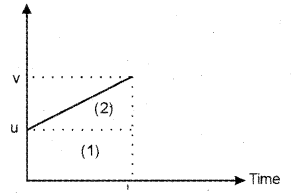
From this graph we get acceleration,
a = Slope of the graph
a = \(\frac { v – u }{ t }\)
at = v – u
v =u + at ……(1)
The area under velocity – time gives displacement.
ie : displacement S = area of triangle (2) + area of rectangle (1)
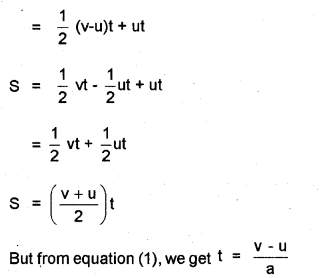
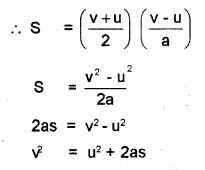
Question 3.
A physical quantity having both magnitude and direction is a vector and if it has only magnitude it is a scalar. Categories the following physical quantities into scalars and vectors. (MAY-2011)
a) Force
b) Angular momentum
c) Time
d) Work
Answer:
Vector : Force, Angular momentum
Scalar : Time, work.
Question 4.
Acceleration is the time rate of change of velocity. Give an example of a body possessing zero velocity and still accelerating. (MAY-2011)
Answer:
i) An oscillating pendulum at extreme position,
ii) At highest point of a stone that is thrown vertically upwards with a velocity.
Question 5.
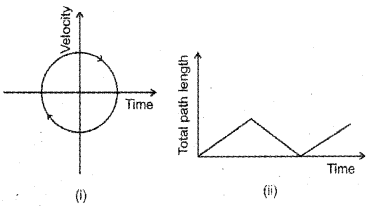
Graph representing the motion of two bodies are shown below. State with reason whether it can rep-resent one dimensional motion. (MAY-2011)
Answer:
i) Figure does not represent one dimensional motion. In one dimensional motion velocity can’t have two values at a given time.
ii) Figure also does not represent one dimensional motion. Total path length does not decrease with time.
Question 6.
Acceleration – time graph of a body starts from rest as shown below: (MARCH-2012)
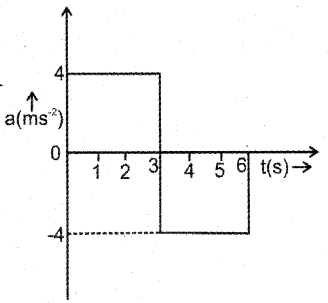
a) What is the use of the acceleration – time graph?
b) Draw the velocity-time graph using the above graph
c) Find the displacement in the given interval of time from 0 to 3 seconds.
Answer:
a) i) The area of acceleration – time graph gives change in velocity.
ii) From a-t graph we can find instantaneous acceleration.
iii) Slope of a-t (acceleration-time) graph gives rate of change of acceleration or jerk.
b)
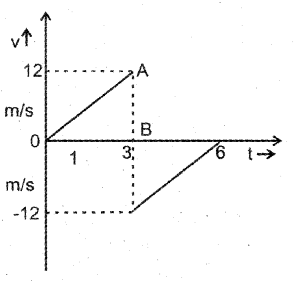
c) Displacement = Area under graph
= Area of ∆ OAB
= 1/2 x 3 x 12
= 18m
Question 7.
a) State in the following cases whether the motion is one, two or three dimensions. (MAY-2012)
i) A butterfly flying around a flower.
ii) A bus moving along a long and straight road.
b) Derive the equations of motion for non-uniform motion in one dimension.
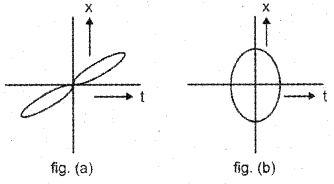
c) Look at the graphs in fig. (a) and fig. (b) carefully and state which of these can’t possibly represent one dimensional motion with reasons.
Answer:
a) 1) 3 D
2) 1 D
b) Velocity – time relation
Consider a body moving along a straight line with uniform acceleration ‘a’. Let ‘u’ be initial velocity and ‘v ‘ be the final velocity at time t.

We know acceleration a = \(\frac { Change in velocity }{ Time interval }\)
a= \(\frac { v – u }{ t }\)
at = v-u
v = u+at
Position-time relation
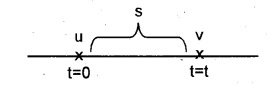
Consider a body moving along a straight line with uniform acceleration a. Let ‘u’ be initial velocity and ‘v’ be the final velocity. ‘S’ is the displacement travelled by the body during the time interval T.
Displacement of the body during the time interval t,
s = average velocity x time
s = \(\frac { v + u }{ 2 }\) t ……..(1)
But v = u + at ……….(2)
Substitute eq(2) in eq(1) we get
s = ut + 1/2 at²
Position velocity relation
s = \(\frac { v + u }{ 2 }\) t ………(1)
But we know v = u + at
\(\frac { v – u }{ a }\) = t ………..(2)
Substitute eq(2) in eq(1)
v² = u² + 2as
c) At a griven instant of time, the particle will have two positions. Which is not possible. Hence fig(a) is not possible fig (b) does not represent one dimensional motion. At a given instant of time, the particle will have two values of velocity in positive as well as negative direction which is not possible in one dimensional motion.
Question 8.
Figure given below shows the motion of a school bus starting from the point 0 and travels along a straight line. (MARCH-2013)
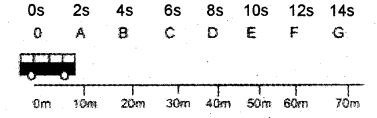
a) Complete the following table:

b) Is the motion of the bus uniform or nonuniform? Justify your answer.
c) Draw the position-time graph of the above motion.
d) A student in the school bus notices the speedometer of the bus. Which type of speed is shown by the speedometer?
Answer:
a) i) velocity = \(\frac { displacement }{ time }\)
= \(\frac { 10}{ 2 }\)
= 5 m/s
ii) Displacement = Velocity x time
= 5 x 10
= 50 m
b) Bus is moving with uniform velocity. Hence this motion is uniform motion.
c)

d) Instantaneous speed.
Question 9.
Acceleration-time graph of a body is shown below: (MAY-2013)
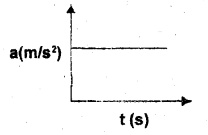
a) Draw the corresponding velocity – time graph.
b) What does the area under the velocity – time graph
represent?
c) Arrive at a relation connecting velocity (v) and time (t) for a uniformly accelerated body.
Answer:
a)
b) Displacement
c) v² = u² + 2as
0 = u² + 2as
s = \(\frac { u² }{ 2a }\)
Question 10.
Acceleration is defined as the rate of change of velocity. (MARCH-2014)
a) Is it possible for a body to have acceleration with-out velocity? Explain.
b) Draw the velocity – time graph of a body moving with uniform acceleration ‘a’ and initial velocity V0.
c) Using the above graph, obtain the equation for displacements time ‘t’.
Answer:
a) Yes
When a vertically projected body reaches at highest point, its velocity becomes zero and acceleration a = g.
b)
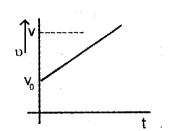
c) Area gives displacement
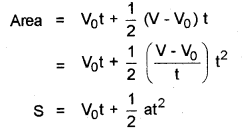
Question 11.
Velocity is defined as the rate of change of displacement. (MAY-2014)
a) Distinguish between average velocity and instantaneous velocity.
b) When does the average velocity become equal to the instantaneous velocity?
c) A car travels from A to Bat 60 km/hr and returns to A at 90 km/hr. What is its average velocity and average speed?
Answer:
a) Average – Velocity is the ratio of total displacement to the total time interval.
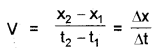
The velocity at an instant is called instantaneous velocity.
v = \(\frac { dx }{ dy }\)
b) In the limit ∆t -> 0,the average velocity becomes instantaneous velocity.
Instantaneous velocity,
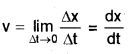
c) Refer Q. No. 5(a), June 2008 to get formula
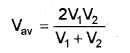
= \(\frac { 2 x 60 x 90 }{ 60 + 90 }\)
= 72 km/h
Question 12.
Position-time graph of a body is given. (MARCH-2015)
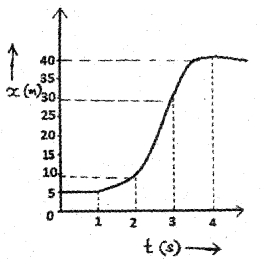
a) Estimate the velocity during the time interval t=2s to t = 3s.
b) Displacement of an object is proportional to t³. Show that its acceleration is increasing with time.
Answer:
Slope of position time graph gives velocity
![]()
b) x = t³
Differentiating on both sides

This equation shows that the acceleration varies with time.
Question 13.
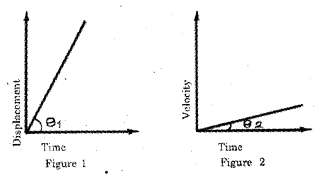
Figure 1 shows displacement time graph of runner A. Figure shows velocity -time graph of runner B. (MAY-2015)
Answer:
a) Identify the type of motion the runner A has.
i) Uniform motion
ii) Nonuniform motion
iii) Accelerated motion
iv) Jerking motion
b) Derive a mathematical relation that connects displacement, velocity and time for runner A.
c) Analyzing the above tow graphs, find which runner will win the race. Why? (Here θ1 > θ2).
a) i, uniform motion
b) v² = u² + 2as
0 = u² + 2as
s = \(\frac { u² }{ 2a }\)
c) Runner A is moving with constant velocity. For runner B, velocity is increasing with time (uniformly accelerated). Hence runner B will win the race.
Question 14.
Velocity – time graph of an object is given below. (MARCH-2016)
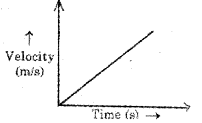
a) What type of motion is indicated by the above graph?
b) Derive a relation connecting the d is placement and time for this type of motion.
c) The ratio of velocity, to speed of an object is
i) one
ii) greater than one
iii) less than one
iv) either less than one or equal to one
Answer:
a) uniform acceleration
b) v² = u² + 2as
0 = u² + 2as
s = \(\frac { u² }{ 2a }\)
c) iv, less than one or equal to one
Question 15.
Velocity – time graph of a body is given below. (MAY-2016)
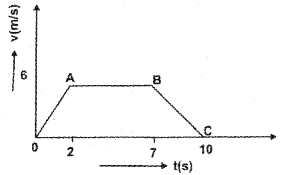
a) Which portion of the graph represents uniform retardation?
i) OA
ii) AB
iii) BC
iv) OC
b) Find the displacement in time 2s to 7s.
c) A stone is dropped from a height h. Arrive at an expression for the time taken to reach the ground.
Answer:
a) iii) BC
b) Area under AB gives displacement between 2s and 7s.
displacement = 6 x 5 = 30 cm
c)
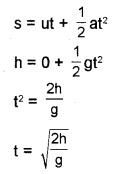
Question 16.
An object released near the surface of the earth is said to be in free fall. (Neglect the air resistance). (MARCH-2017)
a) Choose the correct alternative from the clues given at the end of the statement.
“Free fall is an example of accelerated motion”, (uniformly / non uniformly)
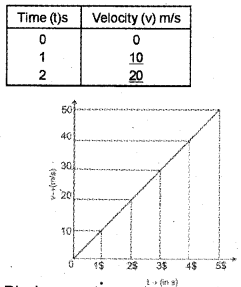
b) The incomplete table shows the velocity (v) of a freely falling object in a time interval of 1 s. (Take g=10m/s²)
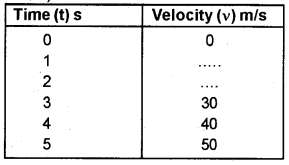
Complete the table and draw the velocity-time graph.
c) Area under velocity-time graph gives….
Answer:
a) Uniformly
b)
c) displacement