Plus One Maths Notes Chapter 5 Complex Numbers and Quadratic Equations is part of Plus One Maths Notes. Here we have given Kerala Plus One Maths Notes Chapter 5 Complex Numbers and Quadratic Equations .
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus One |
| Subject | Maths Notes |
| Chapter | Chapter 5 |
| Chapter Name | Complex Numbers and Quadratic Equations |
| Category | Plus One Kerala |
Kerala Plus One Maths Notes Chapter 5 Complex Numbers and Quadratic Equations
we have studied linear equations in one and two variables and quadratic equations in one variable. We have seen that the equation x2 + 1 = 0 has no real solution since the root of a negative number does not exist in a real number. So, we need to extend the real number system to a larger number system to accommodate such numbers.
I. Complex Numbers
A number of the form a + ib, where a and b are real numbers and i = √-1.
Usually, a complex number is denoted by z, a is the real part of z denoted by Re(z) and b is the imaginary part of z denoted by Im(z).
II. Algebra of Complex Numbers
Addition: Let z1 = a + ib and z2 = c + id be two complex numbers. Then the sum z1 + z2 is obtained by adding the real and imaginary parts.
1. z1 + z2 = z2 + z1, commutative.
2. z1 + (z2 + z3) = (z1 + z2) + z3, associative.
3. 0 + i0 is the identity element.
4. -z is the inverse of z.
Multiplication: Let z1 = a + ib and z2 = c + id be two complex numbers.
Then the product z1z2 is defined as follows:
z1z2 = (ac – bd) + i(ad + bc).
1. z1z2 = z2z1, commutative.
2. z1(z2z3) = (z1z2)z3, associative.
3. 1 + i0 is the identity element.
4. \(\frac{1}{z}\) is the inverse of z.
5. z1(z2 + z3) = z1z2 + z1z3, distributive law.
Power of ‘i’: i3 = -i, i4 = 1
In general i4k = 1, i4k+1 = i, i4k+2 = -1, i4k+3 = -i
Identities:
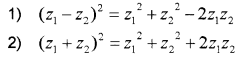
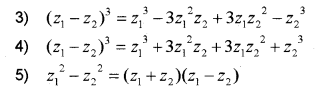
The Modulus and Conjugate of a complex number:
Consider a complex number z = a + ib . Then, the conjugate of z is denoted by \(\bar{z}\), defined as \(\bar{z}\) = a – ib and the modulus of z is denoted by |z|, defined as \(\sqrt{a^{2}+b^{2}}\).
Properties:
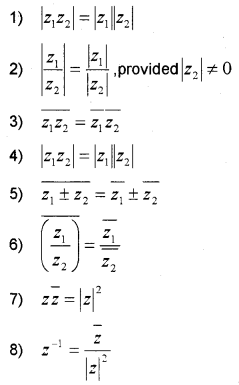
III. Representation of Complex Number
Argand Plane:
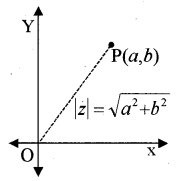
A complex number z = a + ib which corresponds to the ordered pair (a, b) can be represented geometrically as the unique point P(a, b) in the XY-plane, where the real part is taken along the x-axis and the imaginary part along the y-axis. Such a plane is called the Argand Plane or Complex plane.
Polar Form:
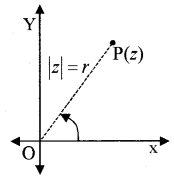
Let the point P represent the non-zero complex number z = x + iy. Let the directed line segment OP be of length ‘r’ and be the angle which OP makes with the positive direction of the x-axis. Then, P is determined by the unique ordered pair of a real number (r, θ) called polar coordinate of the point P, where x = r cos θ, y = r sin θ and therefore the polar form of z can be represented as z = r(cos θ + i sin θ).
The principle argument of z is value ‘θ’ such that -x ≤ θ ≤ π, denoted by arg z.
To find the principle argument, we find tan α = |\(\frac{y}{x}\)|, 0 ≤ α ≤ \(\frac{\pi}{2}\)
| The quadrant on which ‘P’ lies | arg z = |
| I | α |
| II | π – α |
| III | α – π |
| IV | -α |
| Positive real axis | 0 |
| Negative real axis | π |
| Positive imaginary axis | \(\frac{\pi}{2}\) |
| Negative imaginary axis | \(-\frac{\pi}{2}\) |
We hope the Plus One Maths Notes Chapter 5 Complex Numbers and Quadratic Equations help you. If you have any query regarding Kerala Plus One Maths Notes Chapter 5 Complex Numbers and Quadratic Equations, drop a comment below and we will get back to you at the earliest.