Plus One Maths Notes Chapter 13 Limits and Derivatives is part of Plus One Maths Notes. Here we have given Kerala Plus One Maths Notes Chapter 13 Limits and Derivatives.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus One |
| Subject | Maths Notes |
| Chapter | Chapter 13 |
| Chapter Name | Limits and Derivatives |
| Category | Plus One Kerala |
Kerala Plus One Maths Notes Chapter 13 Limits and Derivatives
Calculus is that branch of mathematics which mainly deals with the study of change in the value of a function as the points in the domain changes.
I. Limit
Limit of a function f(x) at x = a is the behaviors of f(x) at x = a.
x → a–: Means that ‘x’ takes values less than ‘a’ but not ‘a’.
x → a+: Means that ‘x’ takes values greater than ‘a’ but not ‘a’.
x → a: Read as ‘x’ tends to ‘a’, means that ‘x’ takes values very close to ‘a’ but not ‘a’.
\(\lim _{x \rightarrow a^{-}} f(x)=A\): Read as left limit of f(x) is ‘A’, means that f(x) → A as x → a–. To evaluate the left limit we use the following substitution \(\lim _{x \rightarrow a^{-}} f(x)=\lim _{h \rightarrow 0} f(a-h)\)
\(\lim _{x \rightarrow a^{+}} f(x)=B\): Read as right limit of f(x) is ‘B’, means that f(x) → B as x → a+. To evaluate the left limit we use the following substitution \(\lim _{x \rightarrow a^{+}} f(x)=\lim _{h \rightarrow 0} f(a+h)\).
If left limit and right limit of f(x) at x = a are equal, then we say that the limit of the function f(x) exists at x = a and is denoted
by lim \(\lim _{x \rightarrow a} f(x)\). Otherwise we say that \(\lim _{x \rightarrow a} f(x)\) does not exist.
II. Evaluation Methods
- Direct substitution method
- Factorisation method
- Rationalisation method
- Using standard results.
III. Algebra of Limits:
For functions f and g the following holds;
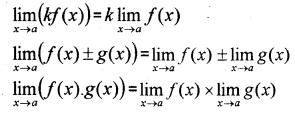
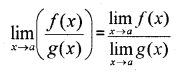
IV. Standard Results
\(\lim _{x \rightarrow a} k=k\), where k is constant.
\(\lim _{x \rightarrow a} f(x)=f(a)\), if f(x) is a polynomial function.
1. \(=\frac{0}{0}\), if possible we can factorise the numerator and denominator and then, cancel the common factors and again put x = a. This factorization method is not possible in all cases so we are studying some standard limits.
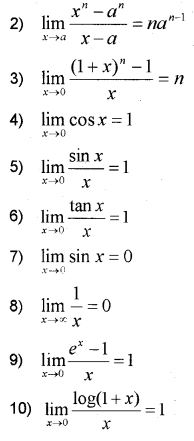
V. Derivatives
A derivative of f at a: Suppose f is a real-valued function and a is a point in its domain of definition. The derivative of f at a is defined by \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)
Provided this limit exists. A derivative of f (x) at a is denoted by f'(a).
Derivative of f at x. Suppose f is a real valued function, the function defined by \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
Wherever this limit exists is defined as the derivative of f at x and is denoted by f”(x) |\(\frac{d y}{d x}\)| |y1| y’. This definition of derivative is also called the first principle of the derivative.
VI. Algebra of Derivatives
For functions f and g are differentiable following holds;

VII. Standard Results
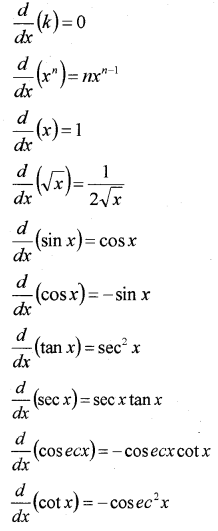
We hope the Plus One Maths Notes Chapter 13 Limits and Derivatives help you. If you have any query regarding Kerala Plus One Maths Notes Chapter 13 Limits and Derivatives, drop a comment below and we will get back to you at th earliest.