Kerala Plus One Maths Improvement Question Paper Say 2018 with Answers
| Board | SCERT |
| Class | Plus One |
| Subject | Maths |
| Category | Plus One Previous Year Question Papers |
Time Allowed: 2 1/2 hours
Cool off time: 15 Minutes
Maximum Marks: 80
General Instructions to Candidates :
- There is a ‘cool off time’ of 15 minutes in addition to the writing time.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read instructions carefully.
- Read questions carefully before you answering.
- Calculations, figures and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non programmable calculators are not allowed in the Examination Hall.
Answer any 6 from questions 1 to 7. Each question carries 3 score. (6 × 1 = 6)
Question 1.
(a) If A = {2, 3, 4, 5} and B = {4, 5, 6, 7}, then write:
(i) A∪B
(ii) A∩B
(b) Which one of the following is equal to {x : x∈R, 2 < x ≤ 4} ?
(i) {2, 3, 4} (ii) {3, 4} (iii) [2, 4] (iv) (2, 4]
Answer:
(a) (i) A∪B = {2, 3, 4, 5, 6, 7}
(ii) A∩B = {4, 5}
(b) (iv) (2, 4]
Question 2.
Consider the set A = {x: x is an integer 0 ≤ x < 4}
(a) Write A in Roster from.
(b) If B = {5, 6}, then write A × B
(c) Write the number of possible relations from A to B.
Answer:
(a) A = {0, 1, 2, 3}
(b) A × B = {(0, 5), (0, 6), (1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6)}
(c) Number of relations = 28
Question 3.

Answer:
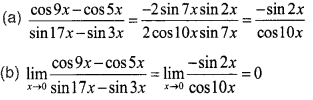
Question 4.
Solve the inequality \(\frac{x}{2} \geq \frac{5 x-2}{3}-\frac{7 x-3}{5}\)
Answer:

Question 5.
Find the Polar form of the complex number \(\frac{1+i}{1-i}\)
Answer:
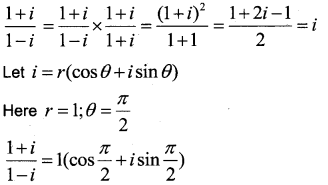
Question 6.
How many terms of the GP, 3, 3/2, 3/4,………….. are needed to give the sum \(\frac{3069}{512}\)
Answer:
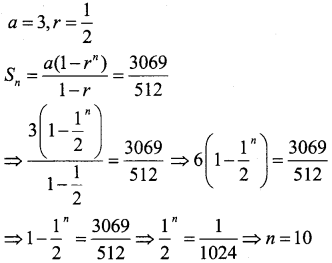
Question 7.
Consider the real valued function
f(x) = \(\frac{x-3}{x^{2}-x-6}\)
(a) Find the domain of f(x).
(b) Evaluate \(\lim _{x \rightarrow 3}\) f(x)
Answer:
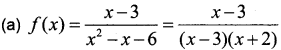
The function is not defined for values x = 3, -2
Hence the domain = R – {3, -2}
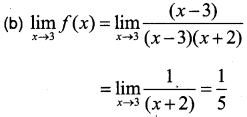
Answer any 8 from questions 8 to 17. Each question carries 4 score. (8 × 4 = 32)
Question 8.
(a) If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8}, B = {2, 3, 5, 7}. Verify (A∪B)’ = A’∩B’
(b) If A and B are two disjoint sets, with n(A) = 4 and n (B) = 2, then n (A – B) = ……..
Answer:
(a) A∪B = {2, 3, 4, 5, 6, 7, 8}
(A∪B)’ = {1, 9}
A’ = {1, 3, 5, 7, 9}, B’ = {1, 4, 6, 8, 9}
A’∩B’ = {1, 9}
(b) n(A – B) = 4
Question 9.
Consider the statement
P(n): 1 + 3 + 32 +………+ 3n-1 = \(\frac{3^{n}-1}{2}\)
(a) Show that P(1) is TRUE
(b) Prove by principle of mathematical induction, that P(n) is TRUE for all n∈N
Answer:
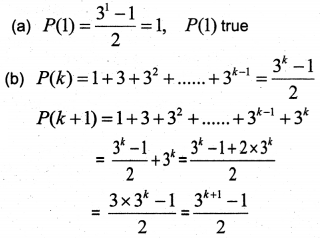
By PMI; true for all natural number n.
Question 10.
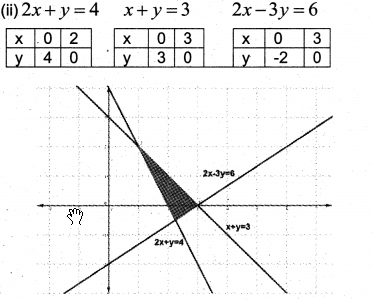
Solve the following inequalities graphically:
2x + y ≥ 4
x + y ≤ 3
2x – 3y ≤ 6
Answer:
Question 11.
Find the square roots of the complex number 3 + 4i
Answer:
Let x + iy = \(\sqrt{3+4 i}\)
Then (x + iy)2 = 3 + 4i
⇒ x2 – y2 + 2 xyi = 3 + 4i
Equating real and imaginary parts, we have
x2 – y2 = 3 ………(1)
2xy = 4
We know the identity
(x2 + y2)2 = (x2 – y2)2 + (2xy)2
= 9 + 16 = 25
Thus, x2 + y2 = 5 ………(2)
From (1) and (2), x2 = 4 and y2 = 1 or x = ±2 and y = ±1
Since the product xy is positive, we have x = 2, y = 1 or, x = – 2, y = -1
Thus, the square roots of 3 + 4i are 2 + i and -2 -i.
Question 12.
(a) Insert five numbers between 8 and 26 such that the resulting sequence is an AP.
(b) Find the sum to n terms of the series 1 × 2 + 2 × 3 + 3 × 4 + ……….
Answer:
(a) a = 8, a7 = 26
a + 6d = 26 ⇒ 8 + 6d = 26 ⇒ d = 3
Therefore AP is 8, 11, 14, 17, 20, 23, 26
(b) Given; 1 × 2 + 2 × 3 + 3 × 4 + ….
tn = n(n + 1)
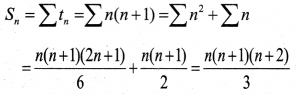
Question 13.
(a) Find the equation of the perpendicular bisector of the line joining the points (0, 0) and (-3, 4).
(b) Find the coordinate of the points on the line y = 3x – 2 that is equidistant from (0, 0) and (-3, 4)
Answer:
(a) Perpendicular bisector passes through the mid point (\(\frac{-3}{2}\), 2)
Slope of the line joining (0, 0) and (-3, 4)
= \(\frac{4-0}{-3-0}=\frac{-4}{3}\)
Slope of perpendicular bisector = \(\frac{3}{4}\)
The equation of the perpendicular bisector is
y – 2 = \(\frac{3}{4}\)(x + \(\frac{3}{2}\))
⇒ y – 2 = \(\frac{3}{8}\)(2x + 3)
⇒ 8y – 16 = 6x + 9
⇒ 6x – 8; y + 25 = 0
(b) The point equidistant from (0, 0) and (-3, 4) is the meeting point of above line and the line y = 3x – 2
Solving 6x – 8y + 25 = 0 and y = 3x + 2
6x – 8(3x + 2) + 25 = 0
⇒ 6x – 24x – 16 + 25 = 0
⇒ 18x = -9 ⇒ x = \(\frac{1}{2}\)
y = 3 × \(\frac{1}{2}\) + 2 = \(\frac{7}{2}\)
Question 14.
(a) Reduce the equation x – y = 4 into normal form.
(b) Write the distance of this line from origin.
Answer:
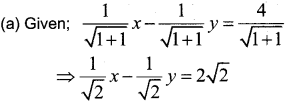
Comparing with the normal form xcos ω + ysin ω = p, we have
cos ω = \(\frac{1}{\sqrt{2}}\); sin ω = –\(\frac{1}{\sqrt{2}}\)
Therefore ω should line in the fourth quadrant
ω = \(-\frac{\pi}{4}\)
Hence normal form is
x cos(\(-\frac{\pi}{4}\)) + y sin(\(-\frac{\pi}{4}\)) = 2\(\sqrt{2}\)
(b) Distance of the line from the origin is p = 2\(\sqrt{2}\)
Question 15.
(a) Find the derivative of f(x) = x sinx with respect to x.
(b) Find the derivative of the function y = \(\sqrt{x}\) with respect to x by using first principles.
Answer:
(a) f(x) = x sinx
f'(x) = x cos x + sin x(1) = x cos x + sin x
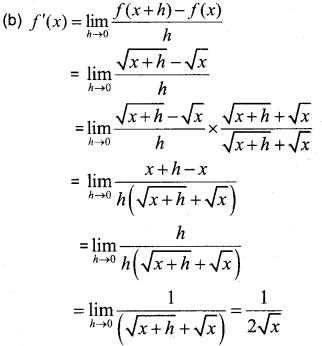
Question 16.
Consider the point A (3, 8, 10) and B (6, 10, -8)
(a) Find the ratio in which the line segment joining A and B is divided by the YZ coordinate plane.
(b) Find the coordinates of the point of division.
(c) Which coordinate plane divides the line segment AB internally? Justify your answer.
Answer:
(a) Let the ration be k : 1.
Point of division is
\(\left(\frac{6 k+3}{k+1}, \frac{10 k+8}{k+1}, \frac{-8 k+10}{k+1}\right)\)
Since the line joining A and B divides YZ plane, the point of intersection has x coordinate equal zero.
\(\frac{6 k+3}{k+1}\) = 0 ⇒ 6k + 3 = 0 ⇒ k = –\(\frac{1}{2}\)
Hence YZ plane divides externally in the ration 1 : 2.
(b) Substituting the value of k, we get the point.

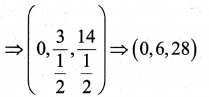
(c) The point A (3, 8, 10) and B (6, 10, -8) have z coordinates opposite in sign. So the point A will lie above and point B will lie below XY plane. Hence XY plane divide the line segment joining A and B internally.
Question 17.
(a) Write the contrapositive of the statement: “If the integer n is odd, then n2 is odd.”
(b) Prove by the method of contradiction: “\(\sqrt{7}\) is irrational.”
Answer:
(a) Contrapositive of the statement:
“If n2 is not an odd integer, then n is not odd.”
(b)Assume that \(\sqrt{7}\) is rational. Then \(\sqrt{7}\) can be written in the form \(\sqrt{7}\) = \(\frac{p}{q}\), where p and q are integers without common factors.
Squaring; 7 = \(\frac{p^{2}}{q^{2}}\) ⇒ 7q2 = p2
⇒ 7 divides p2 ⇒ 7 divides p
Therefore, p = 7k for some integer k.
⇒ p2 = 49k2 ⇒ 7q2 = 49k
⇒ q2 = 7k2
⇒ 7 divides q2 ⇒ 7 divides q
Hence p and q have common factor 7, which contradicts our assumption.
Therefore, \(\sqrt{7}\) is irrational.
Answer any 5 from questions 18 to 24. Each question carries 6 score. (5 × 6 = 30)
Question 18.
(a) If \(\left(\frac{x+3}{2}, \frac{y-1}{3}\right)\) =(4, 2), find the value of x and y.
(b) consider the funetion f(x) = |x| – 3, draw the graph or f(x)
(c) write the domaln and range of f(x).
Answer:
(a) \(\frac{x+3}{2}\) = 4; \(\frac{y-1}{3}\) = 2
⇒ x + 3 = 8; y – 1 = 6
⇒ x = 5; y = 7
(b)
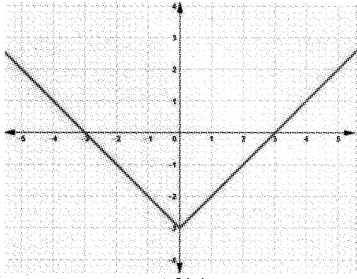
(c) From the graph of f(x) the domain and range is clear.
Domain = R
Range =[-3, ∞)
Question 19.
(a) Find the value of sin(75°)
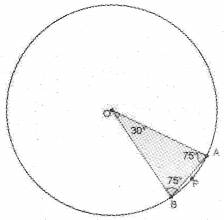
(b) In the given figure and radius of the circle 2 units. Find the length of arc APB.
(c) Find the length of chord AB.
Answer:
(a) sin(75°) = sin(45° +30°)
= sin 45° cos 30° + cos 45° sin 30°
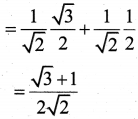
(b) l = rθ = 2 × \(\frac{\pi}{6}\) = \(\frac{\pi}{3}\) units
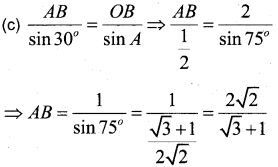
Question 20.
(a) Find the number of words with or without meaning, which can be made by using all the letters of the word ‘GANGA’.
(b) If these words are written as in a dictionary, what will be the 26th word?
(c) A group consists of 4 girls and 7 boys. In how many ways, can a team of 5 members be selected if the team should have at least 3 girls?
Answer:
(a) In the word GANGA, A and G are repeated

Now 25th word is NAAGG
26th word is NAGAG
(c) 3 Girls and 2 boys
= 4C3 × 7C2 =4 × \(\frac{7 \times 6}{1 \times 2}\) = 84
4 Girls and 1 boys = 4C4 × 7C1 = 1 × 7 = 7
Number for groups with at least 3 girls is 84 + 7 = 91
Question 21.
(a) Write the expansion of (a + b)n
(b) Find the coefficient of x5 y7 in the expansion of (x – 2y)12,
(c) Show that 9n+1 – 8n – 9 is divisible by 64.
Answer:
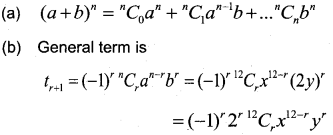
For coefficient of x5 y7 we have r = 7.
Hence coefficient =(-1)7 27 12C7
(c) We have;

Question 22.
Focii of the ellipse in the given figure are (±\(\sqrt{12}\), 0) and vertices are (±4, 0)
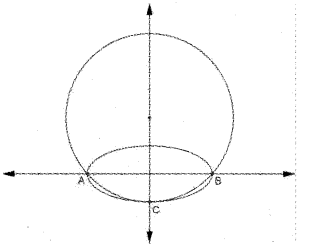
(a) Find the equation of the ellipse.
(b) Write the equation of a circle with centre (0, k) and radius r.
(c) The circle in the figure passes through the points A, B and C on ellipse. Find the equation of a circle.
Answer:
(a) Given, a = 4; c = \(\sqrt{12}\)
c2 = a2 – b2 ⇒ 12 = 16 – b2
⇒ b2 = 16 – 12 = 4
Equation of the ellipse is \(\frac{x^{2}}{16}+\frac{y^{2}}{4}\) = 1
(b) Equation of the circle is x2 + (y – k)2 = r2
We know that the coordinate of C can be obtained by putting x = 0 in the equation of ellipse.
0 + \(\frac{y^{2}}{4}\) = 1 ⇒ y = 2, -2
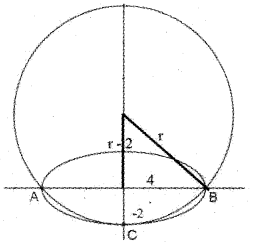
(r – 2)2 = r2 – 42
⇒ r2 – 4r – 4 = r2 – 42
⇒ r = 5
Centre is (0, 3)
Equation of the circle is
x2 + (y – 3)2 = 52
Question 23.
Consider the following table:
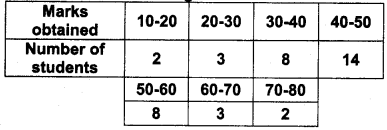
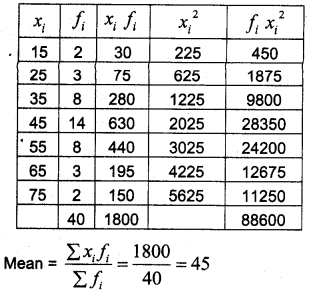
(a) Find the arithmetic mean of marks given in the above data.
(b) Find the standard deviation of marks in the above data.
(c) Find the coefficient of variation.
Answer:
(a)

Question 24.
(a) Consider the experiment in which a coin is tossed repeatedly until a head comes up. Write the sample space.
(b) If A and B are two events of a sample space with P(A) = 0.54, P(B) = 0.60 and P(A∩B) = 0.35. Find P(A’∩B’).
(c) 3 cards are drawn from a well shuffled pack of 52 cards. Find the probability that
(i) All the 3 cards are diamond.
(ii) At least one of the cards is non diamond.
(iii) One card is king and two are jacks.
Answer:
(a) S = {H, TH, TTH, TTTH,……}
(b) P(A’∩B’) = P((A∪B)’) = 1 – P(A∪B)
= 1 – P(A) – P(B) + P(A∩B)
= 1 – 0.54 – 0.69 + 0.35
= 1 – 0.88 = 0.12
(c) (i) All the 3 cards are diamond = \(\frac{{ }^{13} C_{3}}{{ }^{52} C_{3}}\)
(ii) At least one of the cards is non diamond = 1 – \(\frac{{ }^{13} C_{3}}{{ }^{52} C_{3}}\)
(iii) One card is king and two are jacks = \(\frac{{ }^{4} C_{1} \times{ }^{4} C_{2}}{{ }^{52} C_{3}}\)