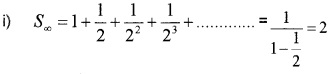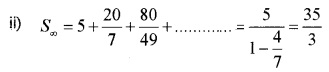Plus One Maths Chapter Wise Questions and Answers Chapter 9 Sequences and Series

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 9 Sequences and Series

Plus One Maths Sequences and Series Three Mark Questions and Answers

Question 1.
The 10^th term of an AP is 73 and the 20^th term is 43. Find the 44^th term.
Answer:
a + 9d = 73 ______(1)
a + 19d = 43 ______(2)
(1) – (2) ⇒ -10d = 30 ⇒ d = -3
(1) ⇒ a + 9(-3) = 73
⇒ a – 27 = 73 ⇒ a = 100
a₄₄ =100 + (44 – 1)(-3) = 100 + (43)(-3) = -29.

Question 2.
The 7^th term of an AP is 34 and the 15^th term is 74. Find the 40^th term.
Answer:
a + 6d = 34 ______(1)
a + 14d = 74 ______(2)
(1) – (2) ⇒ -8d = -40 ⇒ d = 5
(1) ⇒ a + 6(5) = 34 ⇒ a + 30 = 34 ⇒ a = 4
a₄₀ = 4 + (40 – 1)(5) = 4 + (39)(5) = 199.

Question 3.
Find the sum to 32 terms of an AP whose third term is 1 and the 6^th term is -11.
Answer:
a + 2d = 1 ______(1)
a + 5d = -11 ____(2)
(1) – (2) ⇒ -3d = 12 ⇒ d = -4
(1) ⇒ a + 2(-4) = 1 ⇒ a – 8 = 1 ⇒ a = 9
S₃₂ = \(\frac{32}{2}\)(2 × 9 + (32 – 1)(-4))
= 16(18 + (31)(-4)) = 16(18 – 124)
= 16(-106) = -1696.

Question 4.
The sum to n terms of a series is 7n² – 5n. Show that it is an AP and find the 15^th term.
Answer:
Given; S_n = 7n² – 5n
t_n = S_n – S_n-1
= 7n² – 5n – {7(n -1)² – 5(n – 1)}
= 7n² – 5n – {7n² – 14n + 7 – 5n + 5}
= 7n² – 5n – 7n² + 14n – 7 + 5n – 5}
= 14n – 12
Since t_n is linear the given series is an AP.
t₁₅ = 14(15) – 12 = 198.

Question 5.
Find three numbers in AP whose sum is -3 and whose product is 8.
Answer:
Let the three consecutive terms be a – d, a, a + d
a – d + a + a + d = -3 ⇒ 3a = -3 ⇒ a = -1
Given; (-1 – d)(-1)(-1 + d) = 8
⇒ (-1 – d)(-1)(-1 + d) = 8
⇒ (1 – d²)(-1) = 8 ⇒ 1 – d² = -8
⇒ d² – 9 ⇒ d = -3, 3
The AP is 2, -1, -4 or -4, -1, 2.

Question 6.
Find three numbers in AP whose sum is 21 and product is 231.
Answer:
Let the three consecutive terms be a – d, a, a + d
a – d + a + a + d = 21 ⇒ 3a = 21 ⇒ a = 7
Given; (7 – d)(7)(7 + d) = 231
⇒ (7 – d)(7 + d) = 33
⇒ 49 – d² = 33 ⇒ d² = 16 ⇒ d = -4, 4
The AP is 11, 7, 3 or 3, 7, 11.

Question 7.
Find the sum of all natural numbers between 100 and 1000 which are multiple of 5.
Answer:
105 will be the starting number and will end in 995.
⇒ 105 + (n – 1)5 = 995
⇒ (n – 1)5 = 890 ⇒ n – 1 = 178 ⇒ n = 179
S₁₇₉ = \(\frac{179}{2}\)(t₁ + t_n) = \(\frac{179}{2}\)( 105 + 995)
\(\frac{179}{2}\)(1100) = 98450.

Question 8.
If the AM and GM between two numbers are 34 and 16 respectively. Find the numbers.
Answer:
Let the numbers be a and b.

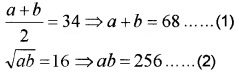
(2) ⇒ a(68 – a) = 256 ⇒ 68a – a² = 256
⇒ a² – 68a + 256 = 0
⇒ a² – 64a – 4a + 256 = 0
⇒ (a – 64)(a – 4) = 0 ⇒ a = 64, 4
When a = 64, b = 4 and when a = 4, b = 64.

Question 9.
If the p^th, q^th and r^th terms of a GP are a, b, c respectively, show that a^q-r b^r-p c^p-q = 1.
Answer:
t_p = AR^p-1 = a; t_q = AR^q-1 = b; t_r = AR^r-1 = c

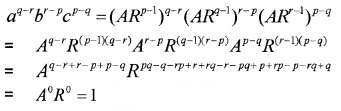
Plus One Maths Sequences and Series Four Mark Questions and Answers

Question 1.
The sum of the first p,g,r terms of an AP are a,b,c respectively, prove that

Answer:
Given;

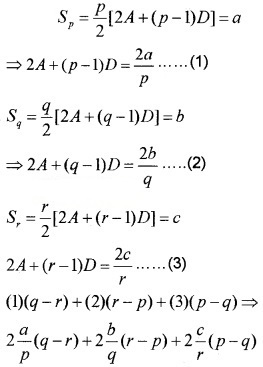
= 2A{q – r + r – p + p – q} + {(q – r)(p – 1) + (r – p)(q – 1) + (p – q)(r – 1)}D

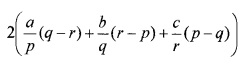
= 2A{0} + {qp – rp – q + r + rq – pq – r + p + pr – qr – p – q}D
= 0 + {0}D = 0
⇒ \(\frac{a}{p}\)(q – r) + \(\frac{b}{q}\)(r – p) + \(\frac{c}{r}\)(p – q) = 0.

Question 2.
The ratio between the sums to n terms of two AP is 7n + 1: 4n + 27. Find the ratio of their 11^th terms.
Answer:

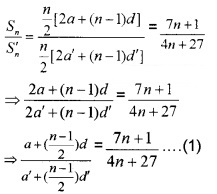
For 11^th term \(\frac{n-1}{2}\) = 10 ⇒ n = 21
Put n = 21 in (1), we have;

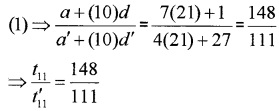
Question 3.
If the sum of p terms of an AP is the same as the sum of its q terms, show that the sum of its (p+q) terms is zero.
Answer:
Given; S_p = S_g
⇒ \(\frac{P}{2}\)[2a + (p – 1 )d] = \(\frac{q}{2}\)[2a + (q – 1 )d]
⇒ 2ap + (p – 1)pd = 2aq + (q – 1 )qd
⇒ 2a(p – q) + (p² – p – q² +q)d = 0
⇒ 2a(p – q) + (p² – q² – (p – q))d = 0
⇒ (p – q){2a + (p + q – 1)d} – 0
⇒ {2a + (p + q – 1 )d} = 0
⇒ \(\frac{p+q}{2}\){2a + (p + q – 1 )d} = 0
⇒ S_p+q = 0.

Question 4.
The sum of the first two terms of a GP is -4 and the fifth term is 4 times the third term.

1. Find the first term and the common ratio. (2)
2. Find the GP. (2)

Answer:
1. Given; S₂ = -4
a + ar = -4 ⇒ a(1 + r) = -4 _____(1)
Also given; t₅ = 4t₃ ⇒ ar⁴ = Aar²
⇒ r² = 4 ⇒ r = ±2
When r = 2(1) ⇒ a(1 + 2) = -4 ⇒ a = \(-\frac{4}{3}\)
When r = -2 (1) ⇒ a(1 – 2) = -4 ⇒ a = 4

2. When r= 2; GP is \(-\frac{4}{3},-\frac{8}{3},-\frac{16}{3}, \dots\)
When r = – 2; GP is 4, -8, 16,…

Question 5.
The sum of three numbers in GP is 38 and their product is 1728. Find the GP.
Answer:
Let the numbers be \(\frac{a}{r}\), a, ar, the given;

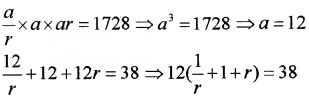
⇒ 6(1 + r + r²) = 19r ⇒ 6 + 6r + 6r² = 19r
⇒ 6r² – 13r + 6 = 0
⇒ 6r² – 9r – 4r + 6 = 0
⇒ 3r(2r – 3) – 2(2r – 3) = 0
⇒ (3r – 2)(2r – 3) = 0
⇒ r = \(\frac{2}{3}, \frac{3}{2}\)
Therefore GP is 8, 12, 18 or 18, 12, 8.

Question 6.
Find the three numbers in GP whose sum is 13 and the sum of whose squares is 91.
Answer:
Let the numbers be \(\frac{a}{r}\), a, ar, the given;

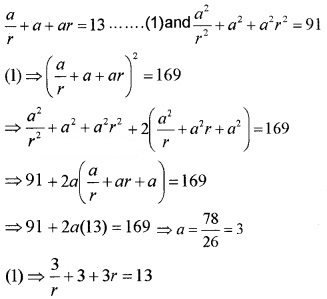
⇒ 3 + 3r + 3r² = 13r ⇒ 3r² – 10r + 3 = 0
⇒ 3r² – 9r – r + 3 = 0
⇒ 3r(r – 3) – (r – 3) = 0
⇒ (3 r – 1)(r – 3) = 0 ⇒ r = 3, \(\frac{1}{3}\)
Therefore the numbers are 1, 3, 9 and 9, 3, 1.

Question 7.
Find the sum to n terms of the following series. (4 score each)

1. 1 × 4 + 3 × 7 + 5 × 10 +……….
2. 1 × 2² + 2 × 3² + 3 × 4² +………..
3. \(\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\frac{1}{3 \times 4}+\ldots \ldots\)
4. 1² + 3² + 5²+……….

Answer:
1. The given series is the product of two AP
1 , 3, 5, with t_n = 1 + (n – 1)2 = 2n – 1
4, 7, 10, with t_n = 4 + (n – 1)3 = 3n + 1
Then the n^th term of the given series is
t_n = (2n – 1)(3n + 1) = 6n² – n – 1

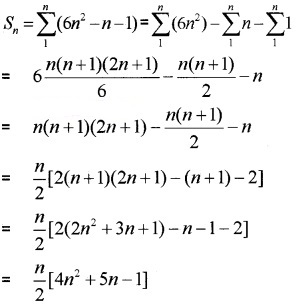
2. The given series has two AP
1, 2, 3,……. with t_n = 1 + (n – 1)1 = n
2, 3, 4,…… with t_n = 2 + (n – 1)1 = n + 1
Then the n^th term of the given series is
t_n = n(n + 1)² = n(n² + 2n + 1) = n³ + 2n² + n

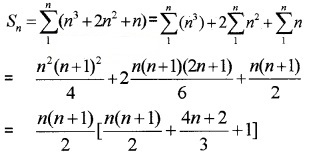
3.

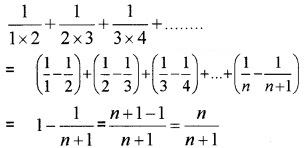
4. The given series has an AP
1, 3, 5……… with t_n = 1 + (n – 1)2 = 2n – 1
Then the n^th term of the given series is
t_n = (2n – 1)² = 4n² – 4n + 1

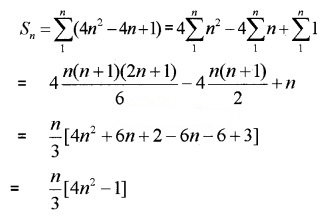
Question 8.
(i) n^th term of some sequence are given below. Which term can be the n th term ofanAP? (1)
(a) a_n = n(n + 1)
(b) a_n = 2 + 5n
(c) a_n = 2ⁿ + 2
(d) a_n = n² + n + 1
(ii) If the sum of 12^th and 22^nd terms of an AP is 100. Find the sum of first 33 terms. (3)
Answer:
(i) (b) a_n = 2 + 5n.

(ii) t₁₂ + t₂₂ = 100 ⇒ a + 11d + a + 21d = 100
⇒ 2a + 32d = 100

Plus One Maths Sequences and Series Six Mark Questions and Answers

Question 1.
1. The product of first 3 terms of a GP is 1000. If 6 terms to the second term and 7 is added to the third term, the terms become an AP.
(a) Find the second term of GP. (1)
(b) Find the terms of the GP. (2)
2. Find the sum of n terms of the series 7 + 77 + 777 +…………… (3)
Answer:
1. (a) \(\frac{a}{r}\) × a × ar = 1000 ⇒ a = 10
(b) \(\frac{a}{r}\), a + 6, ar + 7 from an AP
(a + 6) – \(\frac{a}{r}\) = (ar + 7) – (a + 6)
16 – \(\frac{10}{r}\) = 10r + 7 – 16
⇒ 16r – 10 = 10r² – 9r
⇒ 10r² – 25r + 10 = 0 ⇒ r = 2; \(\frac{1}{2}\)
Hence, 20, 10, 5 and 5, 10, 20;

2. S_n = 7 + 77 + 777 +……………
= 7(1 + 11 + 111 +…………)
= \(\frac{7}{9}\)(9 + 99 + 999 +………..)
= \(\frac{7}{9}\)(10 – 1 + 100 – 1 + 1000 – 1 +………..)
= \(\frac{7}{9}\)(10 + 100 + 1000+……….-1 – 1 – 1-………)

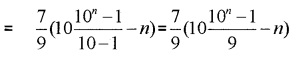
Plus One Maths Sequences and Series Practice Problems Questions and Answers

Question 1.
Find the n^th term of the following sequence (2 score each)

1. 5, 2, -1, -4, -7,…
2. 12, 7, 2, -3, -8,…….

Answer:
1. a = 5; d = 2 – 5 = -3
t_n = a + (n – 1)d = 5 + (n – 1)(-3)
= 5 – 3n + 3 = -3n + 8

2. a = 12; d = 7 – 12 = -5
t_n = a + (n – 1)d = 12 + (n – 1)(-5)
= 12 – 5n + 5 = -5n + 17.

Question 2.
A sequence is given {a_n} by a_n = n² – 1, n ∈ N Show that it is not an AP.
Answer:
Common difference = a_n+1 – a_n
= (n + 1)² – 1 -(n² – 1)
= n² + 2n + 1 – 1 – n² + 1
= 2n + 1.
Common difference is not independent of n so not an AP.

Question 3.
Find the sum to

1. 15 terms of the AP 3, 7, 11,………
2. 20 terms of the AP 10, 7, 4,……..
3. 81 terms of the AP -1, \(\frac{1}{4}, \frac{3}{2}, \ldots \ldots .\) (2 score each)

Answer:
a = 3; d = 7 – 3 = 4

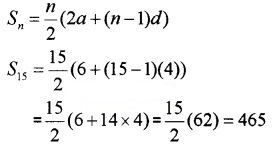
2. a = 10; d = 7 – 10 = -3

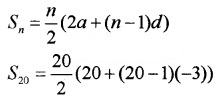
= 10(20 + 19(-3)) =10(-37) = -370

3. a = -1; d = \(\frac{1}{4}\) + 1 = \(\frac{5}{4}\)

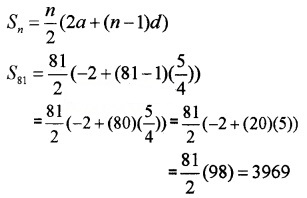
Question 4.
Insert 6 arithmetic means between 3 and 24.
Answer:
Let t₁ = 3, t₂, t₃, t₄, t₅, t₆, t₇, t₈ = 24 be the sequence.
Then;
t₈ = 24 ⇒ a + 7d = 24 ⇒ 3 + 7d = 24
⇒ 7d = 21 ⇒ d = 3
Hence the arithmetic means between 3 and 24 are 6, 9, 12, 15, 18, 21.

Question 5.
If the n^th term of a GP -2, 4, -8, 16 is 1024. Find n.
Answer:
Given; r = \(\frac{4}{-2}\) = -2; t_n = 1024 ⇒ 1024 = ar^n-1
⇒ 1024 = -2(-2)^n-1 ⇒ 1024 = (-2)ⁿ
⇒ (-2)¹⁰ = (-2)ⁿ ⇒ n = 10.

Question 6.
If the n^th term of a GP 2, 2\(\sqrt{2}\), 4,………is 64. Find n.
Answer:
Given; r = \(\frac{2 \sqrt{2}}{2}=\sqrt{2}\);
t_n = 64
⇒ 64 = ar^n-1
⇒ 64 = 2(\(\sqrt{2}\))^n-1

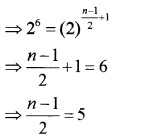
⇒ n = 11.

Question 7.
Find the sum of first 20 terms of the GP \(\sqrt{3}, 2 \sqrt{3}, 4 \sqrt{3}, 8 \sqrt{3}, \ldots \ldots\).
Answer:
Given;

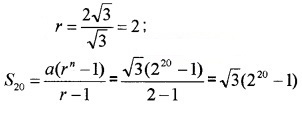
Question 8.
In a GP{a_n}, if a₁ = 3, a_n = 96 and S_n = 189. Find common ratio and n.
Answer:
Given; a₁ = 3, a_n = 96 ⇒ ar^n-1 = 96
⇒ 3 × r^n-1 = 96 ⇒ r^n-1 = 32 = 2⁵
⇒ r^n-1 = 2⁵
Then, r = 2; n = 6.

Question 9.
Find the sum to n terms of the following; (3 score each)

1. 9 + 99 + 999 +………..
2. 4 + 44 + 444 +………..

Answer:
S_n = 9 + 99 + 999 +………..
= 10 – 1 + 100 – 1 + 1000 – 1 +………..
= 10 + 100 + 1000 +…….-1-1-1-…….
= 10 + 10² + 10³ +………-n

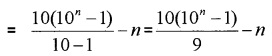
2. S_n = 4 + 44 + 444 +………..
= 4(1 + 11 + 111 +……..)

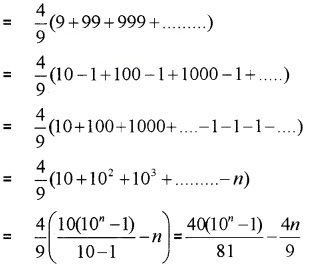
Question 10.
The third term of a GP is 4. Find the product of the first five terms.
Answer:
Given; t₃ = 4 ⇒ ar² – 4
The product of the first five terms
= a × ar × ar² × ar³ × ar⁴
= a⁵r¹⁰ = (ar²)⁵ = 4⁵ = 1024.

Question 11.
Insert 4 geometric means between 4 and 972.
Answer:
Let t₁ = 4, t₂, t₃, t₄, t₅, t₆ = 972 be the sequence. Then;
t₆ = 972 ⇒ ar⁵ = 972 ⇒ 4r⁵ = 972
⇒ r⁵ = 243 = 3⁵ ⇒ r = 3
Hence the arithmetic means between 4 and 972 are 12, 36, 108, 324.

Question 12.
Find the sum to infinity in each of the following Geometric Progression. (2 score each)

Answer:

Plus One Maths Chapter Wise Questions and Answers