Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 7 Permutation and Combinations
Plus One Maths Permutation and Combinations Three Mark Questions and Answers
Question 1.
Find the number of different signals that can be made by arranging at least three flags in order on a vertical pole, if 6 different coloured flags are available.
Answer:
| 3 flags | 6 × 5 × 4 = 120 ways |
| 4 flags | 6 × 5 × 4 × 3 = 360 ways |
| 5 flags | 6 × 5 × 4 × 3 × 2 = 720 ways |
| 6 flags | 6 × 5 × 4 × 3 × 2 × 1 = 720 ways |
Hence the number of different atleast 3 flag signals = 120 + 360 + 720 + 720 = 1920.
Question 2.
2. Find the value of n such that
- nP5 – 42 × nP3, n>4
- (n -1 )P3: nP4 = 1 : 9 (3 score each)
Answer:
1. Given; nP5 = 42 × nP3
⇒ n(n – 1 )(n – 2)(n – 3)(n – 4) = 42 × n(n – 1)(n – 2)
⇒ (n – 3)(n – 4) = 42
⇒ n2 – 7n + 12 = 42
⇒ n2 – 7n – 30 = 0
⇒ (n – 10)(n + 3) = 0
⇒ n = 10; n = -3
The acceptable value is n = 10.
2. Given; 9 × (n – 1)P3 = nP4
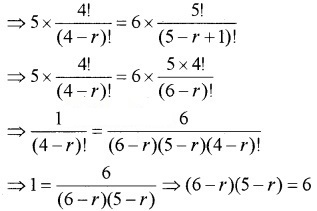
Question 3.
Find the value of r if
- 5 × 4Pr = 6 × 5Pr – 1
- 5Pr = 6Pr – 1 (3 score each)
Answer:
1. Given; 5 × 4Pr = 6 × 5Pr – 1
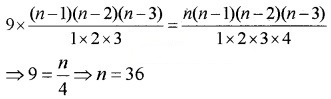
⇒ 30 – 11r + r2 = 6
⇒ r2 – 11r + 24 = 0
⇒ (r – 8)(r – 3) = 0
⇒ r = 8, 3
The acceptable answer is r = 3.
2. Given; 5Pr = 6Pr – 1
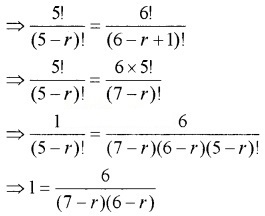
⇒ 42 – 13r + r2 = 6
⇒ r2 – 13r + 36 = 0
⇒ (r – 9)(r – 4) = 0
⇒ r = 9, 4
The acceptable answer is r = 4.
Question 4.
The letters of the word TUESDAY are arranged in a line, each arrangement ends in S.
- How many different arrangements are possible? (2)
- How many of them start with letter D? (1)
Answer:
- In the word TUESDAY there are 7 letters. When word end in S, there are only 6 possible arrangements. This can be done in 6! = 720
- The word start with D and end in S, this can be done in 5! = 120.
Question 5.
Consider the word ANNAMALAI
- How many new words can be formed using the given words? (2)
- Among the new words how many of them will begin with A and end with I. (1)
Answer:
- In the word ANNAMALAI there are 9 letters, of which A appears 4 times, N appears 2 times and the rest ail are different. Therefore the total number of ways is \(\frac{9 !}{4! \times 2 !}\) = 7560.
- The word start with A and end in I, this can be done in \(\frac{7 !}{3! \times 2 !}\) = 420.
Question 6.
Find the rank of the word NAAGI, if these words are written as in a dictionary.
Answer:
The order of the letters will be A, A, G, I, N
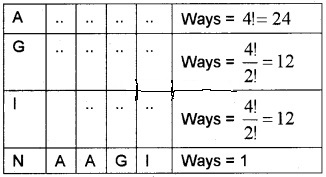
Therefore the position of ‘NAAGI’ is 24 + 12 + 12 + 1 = 49.
Question 7.
A committee of 3 persons is to be constituted from a group of 2 men and 3 women.
- In how many ways can be done? (1)
- How many of these committees would consist of 1 man and 2 women? (2)
Answer:
1. The required number of ways
= 5C3 = 5C2 = \(\frac{5 \times 4}{1 \times 2}\) = 10.
2. One man can be selected in 2C1. 2 women can be selected in 3C2
Therefore required number of ways
= 2C1 × 3C2 = 2 × 3 = 6.
Question 8.
It was found at a certain dinner meeting that after every member had shaken hand with every other members, 45 handshakes were interchanged. How many members were present at the metting?
Answer:
Let n be a member of person present in the meeting. The total number of handshakes is same as the number of ways of selecting 2 persons from among n persons.
The total number of handshakes = nC1 = 45
⇒ \(\frac{n(n-1)}{1 \times 2}\) = 45 ⇒ n2 – n – 90 = 0
⇒ (n – 10)(n + 9) = 0
⇒ n = 10, -9
n = 10 is acceptable.
Question 9.
In an exam, Arjun has to select 4 questions from each part. There are 6, 7 and 8 question in Part I, Part II and Part III, respectively. What is the number of possible combinations in which he can choose the question?
Answer:
Selecting 4 questions from Part I = 6C4 = 6C2
Selecting 4 questions from Part II = 7C4 = 7 C3
Selecting 4 questions from Part III = 8C4
The required number of ways
= 6C2 × 7C3 × 8C4 = 15 × 35 × 70 = 36750.
Plus One Maths Permutation and Combinations Four Mark Questions and Answers
Question 1.
Find the number of different 8-letter arrangements that can be made from the letters of the word DAUGHTER so that
- all vowels occur together. (2)
- all vowels do not occur together. (2)
Answer:
1. DAUGHTER this word has 8 different letters. A, U, E are the vowels. Treat these 3 as one unit, then there are 6 units and can be permuted in 6! ways. The above vowels can be permuted in 3! ways. Hence the total number of words is 6! × 3! = 4320.
2. Number of words all vowels do not occur together = Total number of different words – number of words in which vowels come together
= 8! – 6! × 3! = 6!(8 × 7 – 6) = 2 × 6!(28 – 3)
= 50 × 6! = 36000.
Question 2.
How many permutations are there of the 11 letters in MISSISSIPPI
- taken all together? (2)
- all the I’s not come together? (2)
Answer:
1. In the word MISSISSIPPI there are 11 letters, of which S appears 4 times, I appears 4 times, P appears 2 times and the rest all are different.
Therefore the total number of ways is \(\frac{11 !}{4 ! \times 4 ! \times 2 !}\) = 34650.
2. 4 I’s are kept together and should be counted as one unit, then there are 8 units. The number of ways is \(\frac{8 !}{4 \times 2 !}\) = 840. Therefore the I’s not come together = Total arrangements – 4 I’s together.
= 34650 – 840 = 33810.
Question 3.
Find the number of arrangements of 6 boys and 5 girls in a row so that
- no two girls sit together. (2)
- boys and girls occupy alternate positions. (2)
Answer:
1. Since no two girls sit together, we have first arrange the 6 boys among themselves. This can be done in 6! ways.
![]()
Now no two girls sit together if we place the girls in between boys. There are 7 places and it should be occupied by 5 girls, can be done in 7P5 ways. Therefore the total number of ways is 6! × 7P5 = 720 × 7 × 6 × 5 × 4 × 3 = 1814400.
2. Boys and girls occupy alternate position can be done as follows. First place the boys whose number is large.
![]()
Boys can be arranged in 6! ways. The place between boys can be filled by 5 girls, can be done in 5! ways. Therefore the total number of ways is 6! × 5! = 720 × 120 = 86400.
Question 4.
If the letters of the word DHRONA be permuted and arranged as in a dictionary, find the rank of the word.
Answer:
The order of the letters will be A, D, H, N, O, R
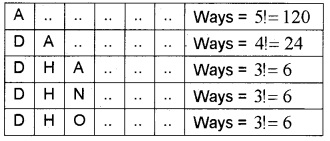
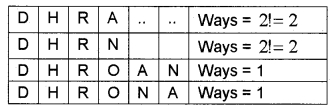
Therefore the position of ‘DHRONA’ is 120 + 24 + 6 + 6 + 6 + 2 + 2 + 1 + 1 = 168.
Question 5.
If the letters of the word MOTHER be permuted and arranged as in a dictionary, find the rank of the word.
Answer:
The order of the letters will be E, H, M, O, R, T
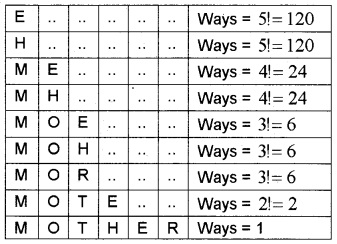
Therefore the position of ‘MOTHER’ is 120 + 120 + 24 + 24 + 6 + 6 + 6 + 2 + 1 = 309.
Question 6.
How many
- Straight line (2)
- Triangles can be formed by joining 12 points, 4 of which are collinear. (2)
Answer:
1. Number of straight lines that can be formed using 12 points = 12C2 = \(\frac{12 \times 11}{1 \times 2}\) = 66. Number of straight lines that can be formed using 4 collinear points = 4C2 = \(\frac{4 \times 3}{1 \times 2}\) = 6. Since the 4 points are collinear, the required number of lines = 66 – 6 + 1 = 61.
2. Number of triangles that can be formed using 12 points = 12C3 = \(\frac{12 \times 11 \times 10}{1 \times 2 \times 3}\) = 220.
Number of triangles that can be formed using 4 collinear points = 4C3 = 4. Since the 4 points are collinear, the required number of triangles = 220 – 4 = 216.
Question 7.
From 7 men and 4 ladies a committee of 6 is to be formed. In how many ways can this be done when the committee contains
- exactly two ladies. (2)
- at least two ladies. (2)
Answer:
1. Exactly two ladies can be selected from 4 in 4C2 = \(\frac{4 \times 3}{1 \times 2}\) = 6. The remaining 4 should be selected from 7 men in 7C4 = \(\frac{7 \times 6 \times 5 \times 4}{1 \times 2 \times 3 \times 4}\) = 35. The required number of ways = 6 × 35 = 210.
2. Atleast 2 ladies can be selected as follows;

The required number of ways = 210 + 140 + 21 = 371.
Question 8.
A box contains 6 apples, 5 oranges, and 8 mangoes.
- In how many ways a fruit is selected from the box. (1)
- In how many different ways can an apple and an orange be selected. (1)
- In how many different ways a person take one apple, one orange, and one mango. (2)
Answer:
- The box contains 6 + 5 + 8 = 19 fruits, from this one fruit can be selected in 19C1 = 19 ways.
- An apple is to be selected from 6 apples and orange be selected from 5 oranges. The required number of ways = 6C1 × 5C1 = 30.
- An apple is to be selected from 6 apples, an orange is to be selected from 5 oranges and one mango is to be selected from 8 mangoes. The required number of ways = 6C1 × 5C 1 × 8C1 = 240.
Question 9.
A student has to answer 6 out of 10 questions which are divided into two parts containing 5 questions each and he is permitted to attempt not more than 4 from any group. In how many ways can he make up his choice?
Answer:
The different possibilities are mentioned below;

The required number of ways
= 5C1 × 5C2 + 5C3 × 5C3 + 5C2 × 5C1
= 5 × 10 + 10 × 10 + 10 × 5 = 200.
Question 10.
- How many chords can be drawn through 15 points on a circle? (2)
- A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected? (2)
Answer:
- Number of chords = 15C2 = \(\frac{15 \times 14}{1 \times 2}\) = 105
- Selection of 2 black and 3 red balls = 5C2 × 6C3 = 10 × 20 = 200.
Question 11.
- If nC2 = nC8 then find n
- Find n if nP5 = 42 × nP3; n> 4
Answer:
1. n = 2 + 8 = 10.
2. DAUGHTER this word has 8 different letters. A, U, E are the vowels. Treat these 3 as one unit, then there are 6 units and can be permuted in 6! ways. The above vowels can be permuted in 3! ways. Hence the total number of words is 6! × 3! = 4320.
Plus One Maths Permutation and Combinations Six Mark Questions and Answers
Question 1.
Find the arrangements of letters of the word INDEPENDENCE. In how many of these arrangements,
- do the words start with P. (2)
- do all the vowels always occur together. (2)
- do the vowels never occur together. (1)
- do the words begin with I and end in P? (1)
Answer:
1. In the word INDEPENDENCE there are 12 letters, of which N appears 3 times, E appears 4 times, D appears 2 times and the rest all are different.
When the words start with P, then there are 11 letters to be filled in 11 spaces. Therefore the total number of ways is \(\frac{11 !}{3! \times 2 ! \times 4 !}\) = 138600.
2. The vowels EEEEI are to be kept together and should be treated as one unit. Then these vowels can be arranged in \(\frac{5 !}{4 !}\) ways. This single unit together with 7 letter will count to units, can be arranged in \(\frac{8 !}{3! \times 2 !}\). Therefore the total number of ways \(\frac{5 !}{4 !} \times \frac{8 !}{3 ! \times 2 !}\) = 16800.
3. Number of ways of arrangement with vowels do not come together = Total arrangement – vowels coming together.
= \(\frac{12 !}{3 ! \times 2 ! \times 4 !}\) – 16800 = 1663200 – 16800 = 1646400.
4. When the words start with I and ends with P, then there are 10 letters to be filled in 10 spaces. Therefore the total number of ways is \(\frac{10 !}{3 ! \times 2 ! \times 4 !}\) = 12600.
Question 2.
Consider the word ASSASSINATION.
- How many permutations are there of the letters of the given word? (2)
- How many different ways can be arranged so that the 4S’s come together? (2)
- How many different ways can be arranged so that the 4S’s do not come together? (1)
- How many begin with A? (1)
Answer:
1. In the word ASSASSINATION there are 13 letters, of which A appears 3 times, S appears 4 times, N appears 2 times, I appears 2 times and the rest all are different. Therefore the total number of ways is \(\frac{13 !}{3! \times 4 ! \times 2 ! \times 2 !}\) = 10810800.
2. 4 S’s are kept together and should be counted as one unit, then there are 10 units. The number of ways is \(\frac{10 !}{3! \times 2 ! \times 2 !}\) = 151200.
3. Number of words in which 4S’s do not come together = Total number of words – 4S’s together = 10810800 -151200 = 10659600.
4. The word will start with any one of the 4 A’s. Then total letter arrange will be 12. Number of words in which begin with A \(\frac{12 !}{2! \times 4 ! \times 2 ! \times 2 !}\) = 2494800.
Question 3.
A team of 11 cricket players is to be chosen from 15 players. In how many ways can this be done so as to:
- Include a particular player A. (2)
- Exclude a particular player B. (2)
- Include A and exclude B. (2)
Answer:
1. A particular player A is to be included, then selection of 10 is to be made from 14 players.
The required number of ways 14C10 = 14C4 = \(\frac{14 \times 13 \times 12 \times 11}{1 \times 2 \times 3 \times 4}\) = 7 × 13 × 11 = 1001.
2. A particular player B is to be excluded, then selection of 11 is to be made from 14 players.
The required number of ways = 14C11 = 14C3 = \(\frac{14 \times 13 \times 12}{1 \times 2 \times 3}\)
= 14 × 13 × 2 = 364.
3. A particular player A is to be included and player B is to be excluded, then selection of 10 is to be made from 13 players. The required number of ways
= 13C10 = 13C3 = \(\frac{13 \times 12 \times 11}{1 \times 2 \times 3}\)
= 13 × 2 × 11 = 286.
Question 4.
What is the number of ways of choosing 4 cards from a pack of 52 playing cards? In how many of these
- four cards are of the same suit, (2)
- are face cards, (1)
- two are red cards and two are black cards, (2)
- cards are of the same colour? (1)
Answer:
Selection of 4 cards from 52 = 52C4
1. There are 4 suits in a pack of 52 playing cards. They are Club, Spade, Diamond, and Heart. Selecting 4 from each can be done in,
= 13C4 + 13C4 + 13C4 + 13C4
= 4 × 13C4 = 4 × \(\frac{13 \times 12 \times 11 \times 10}{1 \times 2 \times 3 \times 4}\) = 2860.
2. There are 12 face cards in a pack of 52 playing cards. Selection 4 cards can be done in 12C4 = 495.
3. There are 26 red cards and 26 black in a pack of 52 playing cards. Selection of 2 cards should be done from each colour, this can be done in 26C2 × 26C2 = (325)2 = 105625.
4. Selection of 4 cards from same colour = 26C4 + 26C4 = 29900
Plus One Maths Permutation and Combinations Practice Problems Questions and Answers
Question 1.
There are 3 routes from place A to place B and 2 routes from place B to place C. Find how many different routes are there from A to C.
Answer:
By fundamental principle of counting, there are 2 × 3 = 6 different ways.
Question 2.
How many 3 digit numbers can be formed from the digits 1, 2 and 3, assuming that the repetition of digits is not allowed.
Answer:
![]()
By fundamental principle of counting, there are 1 × 2 × 3 = 6 different 3 digit numbers.
Question 3.
How many two-digit even numbers with distinct digits can be formed from the digits 1, 2, 3, 4, 5.
Answer:
| filled in 4 ways | filled by 2, 4 – 2ways |
Hence by the fundamental principle of counting, there are 4 × 2 = 8 different 2 digit even numbers.
Question 4.
Evaluate the following
- \(\frac{7 !}{5 !}\)
- \(\frac{12 !}{10 ! \times 2 !}\)
- 6P4
- 9P4
- 10P5
Answer:
1. \(\frac{7 !}{5 !}\) = \(\frac{7 \times 6 \times 5 !}{5 !}\) = 45
2.
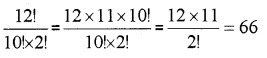
3. 6P4 = 6 × 5 × 4 × 3 = 360
4. 9P4 = 9 × 8 × 7 × 6 = 3024
5. 10P5 = 10 × 9 × 8 × 7 × 6 = 30240
Question 5.
Evaluate the following.
- 10C4
- 21C3
- 19C15
- 31C29 (1 score each)
Answer:
- 10C4 = \(\frac{10 \times 9 \times 8 \times 7}{1 \times 2 \times 3 \times 4}\) = 10 × 3 × 7 = 210
- 21C3 = \(\frac{21 \times 20 \times 19}{1 \times 2 \times 3}\) = 7 × 10 × 19 = 1330
- 19C15 = \(\frac{19 \times 18 \times 17 \times 16}{1 \times 2 \times 3 \times 4}\) = = 19 × 3 × 17 × 4 = 3876
- 31C29 = \(\frac{31 \times 30}{1 \times 2}\) = 465.
Question 6.
How many five digits telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Answer:
Digits 6, 7 already used, so only 8 digits available to fill remaining 3 places.
![]()
Hence by fundamental principle of counting there are 8 × 7 × 6 = 336 different 5 digit telephone numbers.
Question 7.
In how many ways can 5 persons sit in a car, two including the driver in the front seat and 3 in the back seat. If two particular person out of the 5 are to avoid the driver’s seat?
Answer:

Hence by fundamental principle of counting there are 3 × 4 × 3 × 2 × 1 = 72 different ways.
Question 8.
How many numbers can be formed from the digits 1, 2, 3 and 9 if repetition of digits is not allowed?
Answer:
| Single-digit | 4 ways |
| Two-digit | 4 × 3 = 12 ways |
| Three-digit | 4 × 3 × 2 = 24 ways |
| Four-digit | 4 × 3 × 2 × 1 = 24 ways |
Hence the number of total numbers = 4 + 12 + 24 + 24 = 64.
Question 9.
How many 3-digit even numbers can be formed from the digit 1, 2, 3, 4, 5, 6 if the digits can be repeated?
Answer:

Hence by fundamental principle of counting there are 6 × 6 × 3 = 108 different 3 digit even numbers.
Question 10.
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that
- repetition of the digits is allowed? (1)
- repetition of the digits is not allowed (1)
Answer:
1.
![]()
Hence by fundamental principle of counting there are 5 × 5 × 5 = 125 different 3 digit numbers.
2.
![]()
Hence by fundamental principle of counting there are 5 × 4 × 3 = 60 different 3 digit numbers.
Question 11.
How many 8 letter words, with or without meaning, can be formed using the word EQUATION, using each letter exactly once?
Answer:
EQUATION this word has 8 different letters. Different words that can be made from these letters is 81 = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 =40320.
Question 12.
Find the number of ways in which the letters of the word ASSISTANT can be arranged among themselves.
Answer:
In the word ASSISTANT there are 9 letters, of which S appears 3 times, A appears 2 times, T appears 2 times and the rest all are different. Therefore the total number of ways is
\(\frac{9 !}{3! \times 2 ! \times 2 !}\) = 15120.