A Plus Topper

Improve your Grades

Plus One Maths Chapter Wise Questions and Answers Chapter 16 Probability

by

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 16 Probability

Plus One Maths Probability Three Mark Questions and Answers

Question 1.
Two dice are thrown. The events A, B, and C are as follows:

  1. A: getting an even number on the first die.
  2. B: getting an odd number on the first die.
  3. C: getting sum of the numbers on the dice ≤ 5.

Describe the events.
Answer:

  1. A = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
  2. B = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
  3. C = {(1, 1), (1, 2), (2, 1), (2, 2), (1, 3), (3, 1), (2, 3), (3, 2), (1, 4), (4, 1)}

Question 2.
A bag contains 6 red and 12 green balls. Two balls are drawn. What is the probability that one is red and other is green?
Answer:
Here total number of balls = 6 + 12 = 18 Two balls from 18 can be drawn in
18C2 = \(\frac{18 \times 17}{1 \times 2}\) = 153
One red ball out of 6 red can be drawn in 6C1 = 6 ways. One green balls from 12 green may be done in 12C1 = 12 ways.
Therefore, number of favorable cases
= 6 × 12 = 72
The probability that one is red and other is green \(=\frac{72}{153}=\frac{8}{17}\).

Question 3.
In class XI of a school 40% of the students study Mathematics and 30% study Biology, 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.
Answer:
Let M- Mathematics and B – Biology be the events.
P(M) = \(\frac{40}{100}\) = \(\frac{2}{5}\); P(B) = \(\frac{3}{10}\);
P(M ∩ B) = \(\frac{1}{10}\)
P(M ∪ B) = P(M) + P(B) – P(M ∩ B)
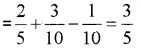
Plus One Maths Chapter Wise Questions and Answers Chapter 16 Probability 3M Q3

Plus One Maths Probability Four Mark Questions and Answers

Question 1.
Two die are rolled, A is the event that the sum of the numbers shown on the two die is 7 and B is the event that at least one of the die shows up 2. Are the two events A and B

  1. Mutually exclusive
  2. Exhaustive.

Answer:
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5),(2,6), (3, 1) , (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
A = {(6, 1), (1, 6), (4, 3), (3, 4), (2, 5), (5, 2)}
B = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (1, 2), (3, 2), (4, 2), (5, 2), (6, 2)}
1. Now; A ∩ B = {(2, 5), (5, 2)} ≠ Φ
Therefore not mutually exclusive.

2. A ∪ B = {(6, 1), (1, 6), (4, 3), (3, 4), (2, 5), (5, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 6), (1, 2), (3, 2), (4, 2), (6, 2)} ≠ S
Therefore not mutually exhaustive.

Question 2.
Letters of the word ASSASSINATION are randomly chosen. Find the probability that letter is

  1. a vowel. (2)
  2. a consonant (2)

Answer:
There 13 letter in the word, with 6 vowels and 7 consonants.
One letter is selected out of 13 in 13C1 = 13 ways.
1. One vowel is selected out of 6 in 6C1 = 6 ways.
Thus the probability of a vowel = \(\frac{6}{13}\).

2. One consonant is selected out of 7 in 7C1 = 7 ways.
Thus the probability of a consonant = \(\frac{7}{13}\).

Question 3.
If E and F are events such that P(E) = \(\frac{1}{4}\), P(F) = \(\frac{1}{2}\) and P(E and F) = \(\frac{1}{8}\). Find

  1. P(E or F)
  2. P(not E and not F)

Answer:
P(E) = \(\frac{1}{4}\), P(F) = \(\frac{1}{2}\); P(E ∩ F) = \(\frac{1}{8}\)
1. P(E ∪ F) = P(E) + P(F) – P(E ∩ F)
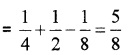
Plus One Maths Chapter Wise Questions and Answers Chapter 16 Probability 4M Q3

2. P(not E and not F) = P(E’ ∩ F’) = P(E ∪ F)’
= 1 – P(E ∪ F) = 1 – \(\frac{5}{8}\) = \(\frac{3}{8}\)

Plus One Maths Probability Practice Problems Questions and Answers

Question 1.
A die is thrown. Describe the following events: (1 score each)

  1. A: a number less than 7.
  2. B: a number greater than 7.
  3. C: a multiple of 3:
  4. D: a number less than 4.
  5. E: An even number greater than 4.
  6. F: a number not less than 3.

Also, find
A ∪ B, A ∩ B, B ∪ C, E ∩ F, D ∩ E, A – C, D – E F’, E ∩ F’.
Answer:

  1. A = {1, 2, 3, 4, 5, 6}
  2. B = Φ
  3. C = {3, 6}
  4. D = {1, 2, 3}
  5. E = {6}
  6. F = {3, 4, 5, 6}

Now; A ∪ B = {1, 2, 3, 4, 5, 6}
A ∩ B = Φ; B ∪ C = {3, 6}, E ∩ F = {6}
F’ = {1, 2}, E ∩ F’ = Φ.

Question 2.
Describe the sample space for the following events: (2 score each)

  1. A coin is tossed and a die is thrown.
  2. A coin is tossed and then a die is rolled.
  3. 2 boys and 2 girls are in a Room X and 1 boy and 3 girls in Room Y. Specify the sample space for the experiment in which a room is selected and then a person.
  4. One die of red colour, one of white colour and one of blue colour are placed in a bag. One die is selected at random and rolled, its colour and the number on its upper most face is noted.
  5. An experiment consists of tossing a coin and then throwing it second time if a head occur. If a tail occurs on the first toss, then a die is rolled once.
  6. A coin is tossed. If the outcome is a head, a die is thrown. If the die shows up shows up an head, a die is thrown. If the die shows up an even number, the die is thrown again.

Answer:
1. A coin is tossed then S1 = {H, T}
A die is rolled then S2 = {1, 2, 3, 4, 5, 6}
Hence sample space
S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}.

2. A coin is tossed then S1 = {H, T}
A die is rolled then S2 = {1, 2, 3, 4, 5, 6}
Hence sample space S = {H1, H2, H3,H4, H5,H6, T}

3. Let B1, B2 denotes the boys and G1, G2 girls in room X, B1 denote the boys and G3, G4, G5 girls in room Y. Hence sample space
S = {XB1, XB2, XG1, XG2, YB1, YG3, XG4, XG5}

4. Three die are R,W, and B, then S1 = {R, W, B)
A die is rolled then S2 = {1, 2, 3, 4, 5, 6}
Hence sample space S = {R1, R2, R3, R4, R5, R6, W1, W2, W3, W4, W5, W6, B1, B2, B3, B4, B5, B6}

5. A coin is tossed then S1 = {H, T}
A coin tossed again then S2 = {H, T}
A die is rolled then S3 = {1, 2, 3, 4, 5, 6}
Hence sample space
S = {HH, HT, T1, T2, T3, T4, T5, T6}

6. A coin is tossed then S1 = {H, T}
When the coin shows T, then there is no action. When the coin shows H, a die is thrown
S2 = {1, 2, 3, 4, 5, 6}
When the die shows {1, 3, 5}, then there is no action.
When the die shows {2, 4, 6}, then a die is thrown again.
Hence;
S = {T, H1, H3, H5, H21, H22, H23, H24, H25, H26, H41, H42, H43, H44, H45, H46,H61, H62, H63, H64, H65, H66}.

Question 3.
A die is rolled. Let E be the event “die shows 4” and F be the event “die shows even number”. Are E and F mutually exclusive?
Answer:
When die is rolled the sample space is S = {1, 2, 3, 4, 5, 6}.
E: die shows 4 = {4}
F: die shows even number = {2, 4, 6}
Now E ∩ F = {4} ≠ Φ
Thus E and F are not mutually exclusive.

Question 4.
Two die are thrown simultaneously. Find the probability of getting 4 as the product.
Answer:
n(S) = 36
A = {(1, 4), (4, 1), (2, 2)}
P(A) = \(\frac{n(A)}{n(S)}=\frac{3}{36}=\frac{1}{12}\).

Question 5.
A coin is tossed, twice, what is the probability that atleast one tail occurs?
Answer:
Here, S = {HH, HT, TH, TT}; n(S) = 4
A = {TH, HT, TT}; n(A) = 3
P(A) = \(\frac{n(A)}{n(S)}=\frac{3}{4}\).

Question 6.
A die is rolled, find the probability of the following events: (2 score each)

  1. A prime number will appear.
  2. A number greater than or equal to 3 will appear.
  3. A number less than or equal to one will appear.
  4. A number more than 6 will appear.
  5. A number less than 6 will appear.

Answer:
Here sample space is S = {1, 2, 3, 4, 5, 6}
1. A: A prime number will appear A = {2, 3, 5};
P(A) = \(\frac{n(A)}{n(S)}=\frac{3}{6}=\frac{1}{2}\)

2. B: A number greater than or equal to 3 will appear. B = {3, 4, 5, 6};
P(B) = \(\frac{n(B)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)

3. C: A number less than or equal to one will appear. C = {1};
P(C) = \(\frac{n(C)}{n(S)}=\frac{1}{6}\)

4. D: A number more than 6 will appear.
D = Φ; P(D) = \(\frac{n(D)}{n(S)}=\frac{0}{6}=0\)

5. E: A number less than 6 will appear. E = {1, 2, 3, 4, 5, 6};
P(E) = \(\frac{n(E)}{n(S)}=\frac{6}{6}=1\).

Question 7.
One card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that (2 score each)

  1. The card drawn is black.
  2. The card drawn is a king.
  3. The card drawn is black and a king.
  4. The card drawn is either black ora king.

Answer:
1. A pack of 52 cards has 26 black cards. So one black card may be drawn in 26 ways. Therefore; the Probability of card drawn is black
= \(\frac{26}{52}=\frac{1}{2}\)

2. A pack of 52 cards has 4 kings. So one king card may be drawn in 4 ways. Therefore; Probability of drawing a king
= \(\frac{4}{52}=\frac{1}{13}\)

3. A pack of 52 cards has 2 black king cards. So one black king card may be drawn in 2 ways. Therefore; Probability of drawing a king
= \(\frac{2}{52}=\frac{1}{26}\)

4. A pack of 52 cards has 26 black cards which include 2 black king and 2 red king cards. So number of cards which are black or king cards
= 26 + 2 = 28.
Therefore; Probability of drawing either a black or king card = = \(\frac{28}{52}=\frac{7}{13}\).

Question 8.
GivenP(A) = \(\frac{3}{5}\) and P(B) = \(\frac{1}{5}\). Find P(A or B), if A and B are mutually exclusive events.
Answer:
Here; P(A) = \(\frac{3}{5}\) and P(B) = \(\frac{1}{5}\)
Since A and B mutually exclusive events
P(A ∪ B) = P(A) + P(B)
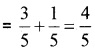
Plus One Maths Chapter Wise Questions and Answers Chapter 16 Probability Practice Questions Q8

Plus One Maths Chapter Wise Questions and Answers