Plus One Maths Chapter Wise Questions and Answers Chapter 15 Statistics

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 15 Statistics

Plus One Maths Statistics Three Mark Questions and Answers

Question 1.
Find the mean deviation about the median for the following data: (3 score each)

1. 13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17.
2. 36, 72, 46, 42, 60, 45, 53, 46, 51, 49.

Answer:
1. Arrange the data in the ascending order we have;
10, 11, 11, 12, 13, 13, 14, 16, 16, 17, 17, 18
Here n = 12. So median is the average of 6^th and 7^th observations.
Therefore; Median, M =\(\frac{13+14}{2}\) = 13.5

Mean deviation = \(\frac{\sum_{i=1}^{n}\left|x_{i}-M\right|}{n}=\frac{28}{12}\) = 2.33

2. Arrange the data in the ascending order we have; 36, 42, 45, 46, 46, 49, 51, 53, 60, 72
Here n = 10. So median is the average of 5^th and 6^th observations.
Therefore; Median, M = \(\frac{46+49}{2}\) = 47.5

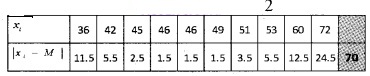
Mean deviation = \(\frac{\sum_{i=1}^{n}\left|x_{i}-M\right|}{n}=\frac{70}{10}\) = 7.

Question 2.
The mean and standard deviation of marks obtained by 50 students of a class in three subjects, mathematics, Physics, and Chemistry are given below:

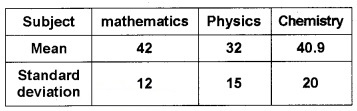
Which of the three subject shows the highest variability in marks and which shows the lowest?
Answer:
For Mathematics:
\(\bar{x}\) = 42, σ = 12
∴ CV of Mathematics = \(\frac{12}{42}\) × 100 = 28.57%
For Physics:
\(\bar{x}\) = 32, σ = 15
∴ CV of Physics = \(\frac{15}{32}\) × 100 = 46.88%
For Chemistry:
\(\bar{x}\) = 40.9, σ = 20
∴ CV of Chemistry = \(\frac{20}{40.9}\) × 100 = 48.9%
Thus Chemistry with highest CV shows highest variability and Mathematics with lowest CV shows lowest variability.

Plus One Maths Statistics Four Mark Questions and Answers

Question 1.
Find the mean deviation about the mean for the following data: (4 scores each)
1.

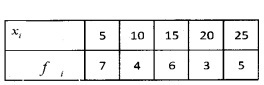
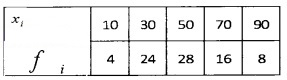
2.

Answer:
1.

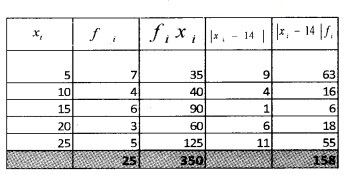
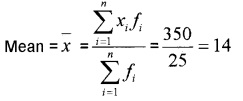
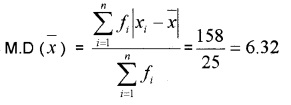
2.

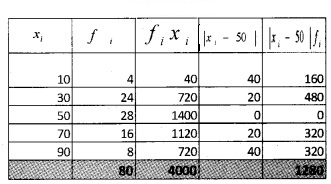
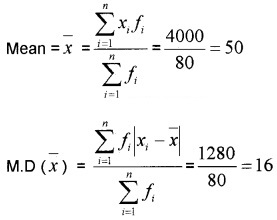
Question 2.
Find the mean deviation about the median for the following data: (4 score each)
1.

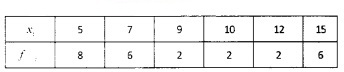
2.

Answer:
1.

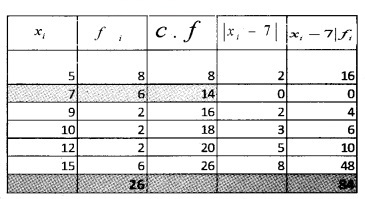
\(\frac{\sum_{i=1}^{n} f_{i}}{2}=\frac{26}{2}\) = 13
The c.f just greater than 13 is 14 and the corresponding value of x is 7. Therefore; median, M = 7
Hence; M.D about median

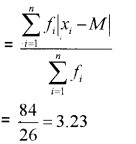
2.

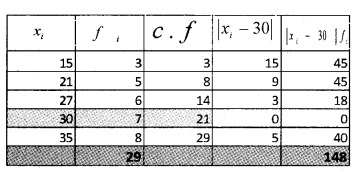
\(\frac{\sum_{i=1}^{n} f_{i}}{2}=\frac{29}{2}\) = 14.5
The c.f just greater than 14.5 is 21 and the corresponding value of x is 30. Therefore; median, M = 30
Hence; M.D about median

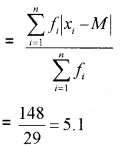
Question 3.
Find the mean deviation about the mean for the following data: (4 score each)
1.

2.

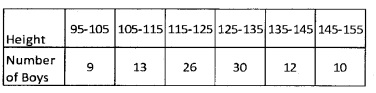
Answer:
1.

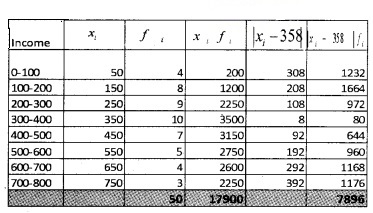
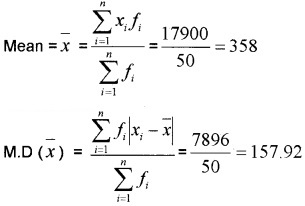
2.

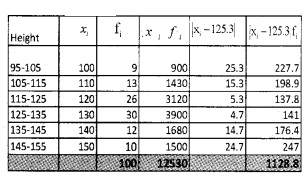
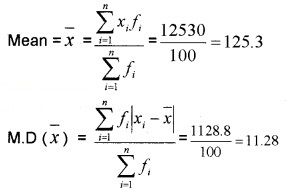
Question 4.
Find the mean deviation about the median for the following data: (4 score each)
1.

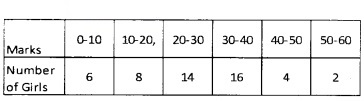
2.

Answer:
1.

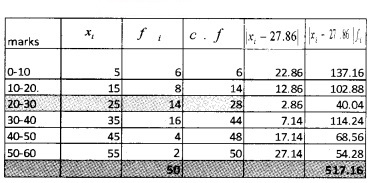
Median class is the class in which the \(\left(\frac{N}{2}\right)^{th}\) observation lies.
\(\frac{N}{2}=\frac{50}{2}\) = 25
Median class = 20 – 30
M = Median

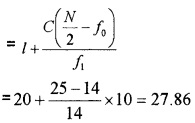
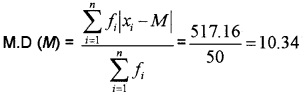
2.

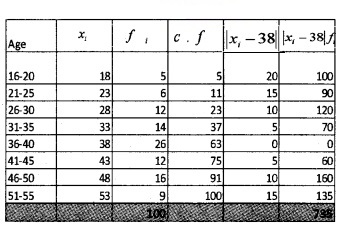
Median class is the class in which the \(\left(\frac{N}{2}\right)^{th}\) observation lies.
\(\frac{N}{2}=\frac{100}{2}\) = 50
Median class = 35.5 – 40.5
M = Median

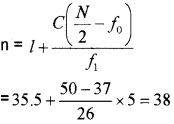
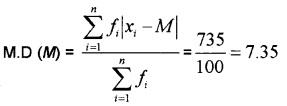
Question 5.
Find the variance and standard deviation of 3, 4, 6, 5, 5, 3, 8, 1, 7, 5
Answer:

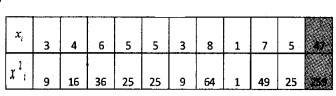
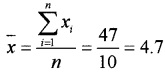
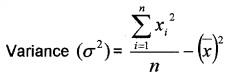
\(\frac{259}{10}\) – (4.7)² = 25.9 – 22.09 = 3.8
Standard Deviation (σ) = \(\sqrt{\text {Variance}}\) = \(\sqrt{3.8}\) =1.95.

Question 6.
Find the variance and standard deviation of

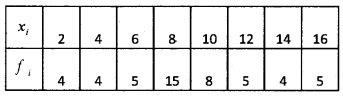
Answer:

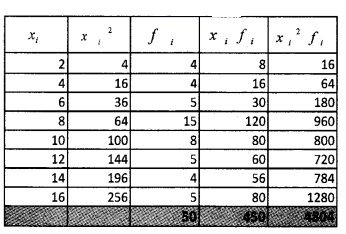
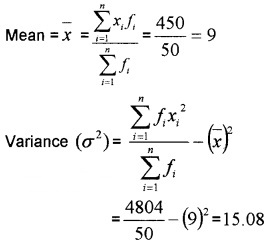
Standard Deviation (σ) = \(\sqrt{\text {Variance}}\)
= \(\sqrt{15.08}\) = 3.88.

Question 7.
An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following result.

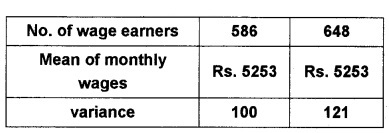
1. Which firm A or B pays larger amount as monthly wages?
2. Which firm A or B, shows greater variability in individual wages?

Answer:
1. Firm: A
Number of wages earners (n₁) = 586
Number of wages earners (\(\bar{x}_{1}\)) = 5253
Total monthly wages = 5253 × 586 = 3078258
Firm: B
Number of wages earners (n₁) = 648
Number of wages earners (\(\bar{x}_{1}\)) = 5253
Total monthly wages = 5253 × 648 = 3403944

2. Since both the firms have same mean of monthly wages, so the firm with a greater variance will have more variability in individual wages. Thus firm B will have more variability in individual wages.

Question 8.
The sum and sum of squares corresponding to length x (in cm) and weight y (in gm) of 50 plant products are given below:

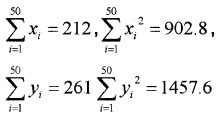
which is more varying, the length or weight?
Answer:
Here,

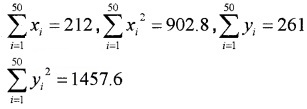
Now

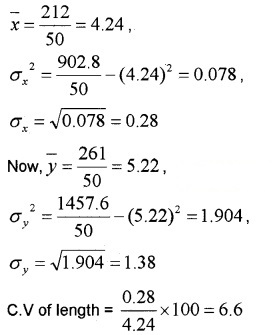
C.V of weight = \(\frac{1.38}{5.22}\) × 100 = 26.44
C.V of weight > C.V of length
Thus weight have more variability than the length

Plus One Maths Statistics Six Mark Questions and Answers

Question 1.
Find the variance and standard deviation of

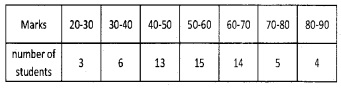
Answer:

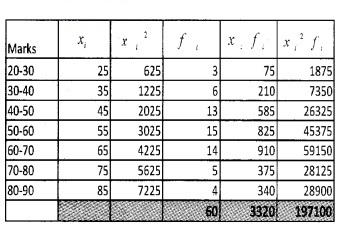
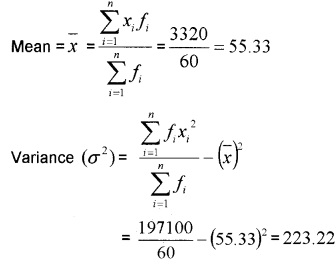
Standard Deviation (a) = \(\sqrt{\text {Variance}}\)
= \(\sqrt{223.22}\) = 14.94.

Plus One Maths Statistics Practice Problems Questions and Answers

Question 1.
Find the mean deviation about the mean for the following data: (2 score each)

1. 4, 7, 8, 9, 10, 12, 13, 17.
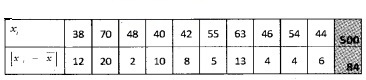
2. 38, 70, 48, 40, 42, 55, 63, 46, 54, 44.

Answer:
1.

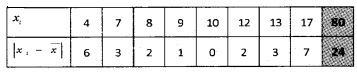
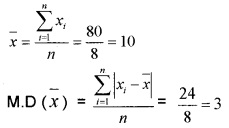
2.

Plus One Maths Chapter Wise Questions and Answers