Plus One Maths Chapter Wise Questions and Answers Chapter 10 Straight Lines

Kerala Plus One Maths Chapter Wise Questions and Answers Chapter 10 Straight Lines

Plus One Maths Straight Lines Three Mark Questions and Answers

Question 1.
Find the equation of the line passing through the point (2, 2) and cutting off intercepts on the axis whose sum is 9.
Answer:
Let equation of the line is \(\frac{x}{a}+\frac{y}{b}\) = 1 ______(1)
Given a + b = 9
Since (1) passes through (2, 2) we have;
\(\frac{2}{b}+\frac{2}{b}\) = 1 ⇒ 2a + 2b – ab ⇒ 2 (a + b) = ab
⇒ 18 = ab. Then the numbers are 3 and 6.
Hence the equation of the line is
\(\frac{x}{3}+\frac{y}{6}\) = 1 ⇒ 6x + 3y = 18 ⇒ 2x + y = 6

OR

\(\frac{x}{6}+\frac{y}{3}\) = 1 ⇒ 3x + 6y = 18 ⇒ x + 2y = 6.

Question 2.
The perpendicular from the origin to a line meets it at the point (-2, 9), find the equation of the line.
Answer:
Slope of the line through the origin and (-2, 9)

Then the slope of the required line is \(\frac{2}{9}\).
Hence the equation is y – y₁ = m(x – x₁)
⇒ y – 9 = \(\frac{2}{9}\)(x – (-2))
⇒ 9y – 81 = 2x + 4 ⇒ 2x – 9x + 85 = 0.

Question 3.
Reduce the following into normal form. (3 score each)

1. \(\sqrt{3}\)x + y – 8 = 0
2. 3x + 3y – 1 = 0

Answer:
1. The given equation can be written in the form \(\sqrt{3}\)x + y = 8
Divide the above equation by

we get;

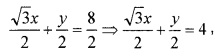
which is the normal form. On comparing with
x cos θ + y sin θ = p
Where; cosθ = \(\frac{\sqrt{3}}{2}\); sinθ = \(\frac{1}{2}\) and p = 4.

2. The given equation can be written in the form 3x + 3y = 1
Divide the above equation by

we get;

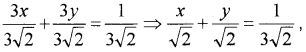
which is the normal form. On comparing with x cosθ + y sinθ = p
Where; cosθ = \(\frac{1}{\sqrt{2}}\); sinθ = \(\frac{1}{\sqrt{2}}\) and p = \(\frac{1}{3 \sqrt{2}}\).

Question 4.
Find the angle between the given lines. (3 score each)

1. y – \(\sqrt{3}\)x – 5 = 0 and \(\sqrt{3}\)y – x + 6 = 0
2. 3x – 2y + 9 = 0 and 2x + y – 9 = 0

Answer:
1. Given; y – \(\sqrt{3}\)x – 5 = 0 and \(\sqrt{3}\)y – x + 6 = 0

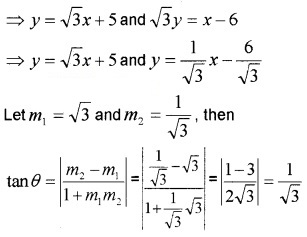
⇒ θ = 30°.

2. Given; 3x – 2y + 9 = 0 and 2x + y – 9 = 0
⇒ 2y = 3x + 9 and y = -2x + 9

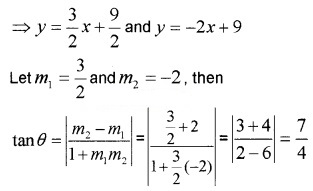
Question 5.
Find the transformed equation of the straight line 2x – 3y + 5 = 0, when the origin is shifted to the point (3, -1) after translation of axes.
Answer:
Let coordinates of a point P changes from (x, y) to (X, Y) in new coordinate axes whose origin has the coordinates h = 3, k = -1. Therefore, we can write the transformation formulae as x = X + 3 and y = y – 1.

Substituting, these values in the given equation of the straight line, we get 2(X + 3) – 3 (Y – 1) + 5 = 0 or 2X – 3Y + 14 = 0. Therefore, the equation of the straight line in new system is 2x – 3y + 14 = 0.

Question 6.
Find what the following equations become when the origin is shifted to the point (1, 1) x² + xy – 3y² – y + 2 = 0.
Answer:
We can write the transformation formulae as x = X + 1 and y = Y+ 1.
The new equation is
(X + 1)² + (X + 1)(Y + 1) – 3(Y + 1)² – (Y + 1) + 2 = 0
X² + XY – 3Y² + 3X – 6Y + 1 = 0
Therefore, the equation of the straight line in new system is x² + xy – 3y² + 3x – 6y + 1 = 0.

Question 7.
1. Identify the figure in which the line has a positive slope. (1)
a.

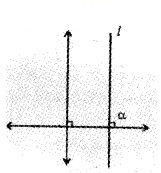
b.

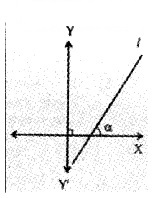
c.

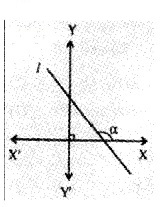
d.

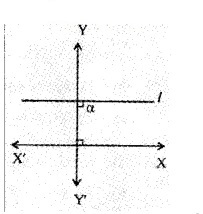
2. Find the x and y intercepts of the line 3x + 4y – 12 = 0 (2)
Answer:
1. Figure b

2. 3x + 4y = 12

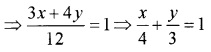
x – intercept = 4; y – intercept = 3.

Plus One Maths Straight Lines Six Mark Questions and Answers

Question 1.
Consider the line 4x – 3y + 12 = 0

1. Find the equation of the line passing through the point (1, 2) and parallel to the given line. (2)
2. Find the distance between these two parallel lines. (1)
3. Which among the following lines is perpendicular to the line 4x – 3y + 12 = 0 (1)
   • 2x + 3y – 8 = 0
   • 4x – 3y + 5 = 0
   • x + y = 7
   • 3x + 4y + 9 = 0

Answer:
1. Equation of the parallel line 4x – 3y + k = 0
Passing through (1, 2)
4(1) – 3(2) + k = 0 ⇒ k = 2
⇒ 4x – 3y + 2 = 0.

2. Distance \(\left|\frac{12-2}{\sqrt{25}}\right|=\frac{10}{5}=2\).

3. 3x + 4y + 9 = 0.

Plus One Maths Straight Lines Practice Problems Questions and Answers

Question 1.
Find the slope of the lines passing through the points (1 score each)

1. (3, -2) and (-1, 4)
2. (4, -5) and (2, 1)
3. (0, -2) and (4, 3)

Answer:
1. Slope

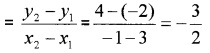
2. Slope

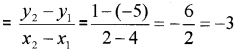
3. Slope

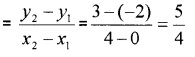
Question 2.
Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
Answer:
Let (x, 0) be the points on the x-axis. Then the distance will be same;
(x – 3)² + 16 = (x – 7)² + 36
⇒ x² – 6x + 9 + 16 = x² – 14x + 49 + 36
⇒ 14x – 6x = 49 + 36 – 9 – 16
⇒ 8x = 60 ⇒ x = \(\frac{15}{2}\)
Hence the point is (\(\frac{15}{2}\), 0).

Question 3.
Find the value of x for which the points (x, -1), (2, 1) and (4, 5) are collinear.
Answer:
The slope of the lines joining the points (x, -1) and (2, 1); (2, 1) and (4, 5) are same.

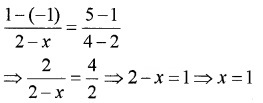
Question 4.
Line through the points (-2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x.
Answer:
The product of the slopes of the lines joining the points (-2, 6) and (4, 8); (8, 12) and (x, 24) will be equal to -1.

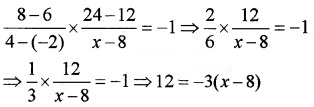
⇒ 12 = -3x + 24 ⇒ 3x = 12⇒ x = 4.

Question 5.
Find the equation the following lines satisfying the given conditions. (2 score each)

1. Passing through the point (-2, 3) with slope -4.
2. Passing through the point (-4, 3) with slope \(\frac{1}{2}\).
3. Line with y-intercept \(-\frac{3}{2}\) and slope \(\frac{1}{2}\)
4. Line with x-intercept – 3 and slope – 2.
5. Line which makes intercepts -3 and 2 on the x- and y-axis respectively.
6. Perpendicular distance from origin is 5 units and the angle the perpendicular makes with the positive direction of x-axis is 30°.
7. Passing through the point (-1, 1) and (2, -4).
8. Passing through the point (1, -1) and (3, 5).

Answer:
1. Equation of the line is y – y₁ = m(x – x₁)
⇒ y – 3 = -4(x – (-2))
⇒ y – 3 = -4x – 8 ⇒ 4x + y + 5 = 0.

2. Equation of the line is y – y₁ = m(x – x₁)
⇒ y – 3 = \(\frac{1}{2}\)(x – (-4))
⇒ 2y – 6 = x + 4 ⇒ x – 2y + 10 = 0.

3. Equation of the line is y = mx + c
⇒ y = \(\frac{1}{2}\) x – \(\frac{3}{2}\) ⇒ 2y = x – 3
⇒ x – 2y – 3 = 0.

4. Equation of the line is y = m(x – d)
⇒ y = -2(x – (-3)) ⇒ y = -2x + 6
⇒ 2x + y = 6.

5. Equation of the line is \(\frac{x}{a}+\frac{y}{b}\) = 1
⇒ \(\frac{x}{-3}+\frac{y}{2}\) = 1 ⇒ 2x – 3y = -6
⇒ 2x – 3y + 6 = 0.

6. Equation of the line is xcosθ + ysinθ = p
⇒ xcos30° + ysin30° = 5

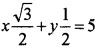
7. Equation of the line is

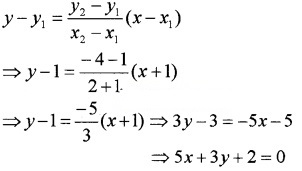
8. Equation of the line is

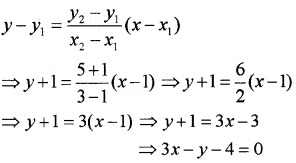
Question 6.
Find the equation of the line passing through the point (-3, 5) and perpendicular to the line through the points (2, 5) and (-3, 6).
Answer:
Slope of the line through the points (2, 5) and (-3, 6)

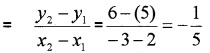
Then the slope of the required line is 5. Hence the equation is y – y₁ = m(x – x₁)
⇒ y – 5 = 5(x – (-3)
⇒ y – 5 = 5x + 15 ⇒ 5x – y + 20 = 0.

Question 7.
Find the equation of the line that cut off equal intercepts on the coordinate axis and passes through the point (2, 3).
Answer:
Let the equal intercept is ‘a’, then equation of the required line is \(\frac{x}{a}+\frac{y}{a}=1\)
Since this line passes through the point (2, 3),
we have; \(\frac{2}{a}+\frac{3}{a}=1\) ⇒ \(\frac{5}{a}\) = 1 ⇒ a = 5
Therefore the equation of the line is \(\frac{x}{5}+\frac{y}{5}=1\)
⇒ x + y = 5.

Question 8.
P(a, b) is the mid-point of a line segment between axis. Show that equation of the line is \(\frac{x}{a}+\frac{y}{a}=2\).
Answer:
Since the P(a, b) is the mid-point of the line segment, then the x-intercept and the y-intercept will be 2a and 2b. Hence the equation of the line is

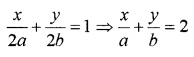
Question 9.
Find the slope, x-intercept and y-intercept of the following lines. (2 score each)

1. 3x – 4y + 10 = 0
2. 6x + 3y – 5 = 0
3. 4x – 3y = 6

Answer:
1. Given the equation of the line is 3x – 4y + 10 = 0 ⇒ 4y = 3x + 10

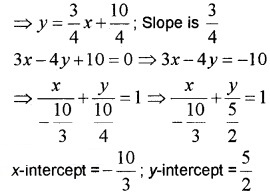
2. Given the equation of the line is 6x + 3y – 5 = 0 ⇒ 3y = -6x + 5

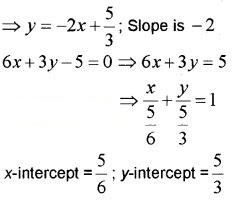
3. Given the equation of the line is
4x – 3y = 6 ⇒ 3y = 4x – 6

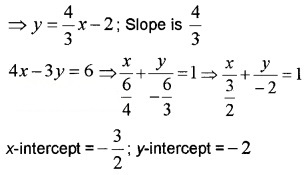
Question 10.
Find the distance between the parallel lines. (2 score each)

1. 3x – 4y + 7 = 0 and 3x – 4y + 5 = 0
2. 15x + 8y – 34 = 0 = 0 and 30x + 16y + 62 = 0

Answer:
1. The distance between the lines 3x – 4y + 7 = 0 and 3x – 4y + 5 = 0

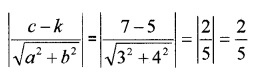
2. The distance between the lines
15x + 8y – 34 = 0 = 0 and 15x + 8y + 31 = 0 is

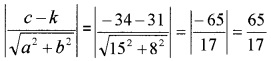
Question 11.
Find the distance between the given point and the line. (2 score each)

1. Line 3x – 4y – 26 = 0 and point (3, -5)
2. Line 12(x + 6) = 5(y – 2)and point(-1, 1)

Answer:
1. The distance between the line and the

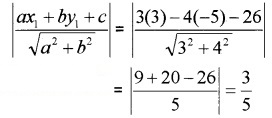
2. Express the line in standard form
12(x + 6) = 5(y – 2) ⇒ 12x + 72 = 5y – 10
⇒ 12x – 5y + 82 = 0
The distance between the line and the point is

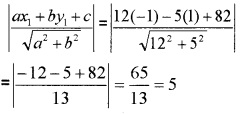
Question 12.
Find the equation of the line parallel to the line 3x – 4y + 2 = Oand passing through the point (-2, 3).
Answer:
The equation of the line parallel to the line 3x – 4y + 2 = 0 is of the form 3x – 4y + k = 0.
Since it passes through (-2, 3), we have;
3(-2) – 4(3) + k = 0 ⇒ -6 – 12 + k = 0
⇒ -18 + k = 0 ⇒ k = 18
Hence the equation is 3x – 4y + 18 = 0.

Question 13.
Find the equation of the line x – 7y + 5 = 0 perpendicular to the line and having x-intercept 3.
Answer:
The equation of the perpendicular line will be 7x + y + k = 0.
Since x-intercept is 3, the line passes through the point (3, 0). So we have;
7(3) + 0 + k = 0 ⇒ 21 + 0 + k = 0 ⇒ k = -21
Therefore the equation is 7x + y – 21 = 0.

Question 14.
Find the new coordinates of point (3, -4) if the origin is shifted to (1, 2) by a translation.
Answer:
The coordinates of the new origin are h = 1, k = 2, and the original coordinates are given to be
x = 3, y = -4
X = x – h; Y = y – k
Substituting the values, we have
X = 3 – 1 = 2 and Y = -4 – 2 = -6
Hence, the coordinates of the point (3, -4) in the new system are (2, – 6).

Plus One Maths Chapter Wise Questions and Answers