Plus One Maths Chapter Wise Previous Questions Chapter 4 Principle of Mathematical Induction

Kerala Plus One Maths Chapter Wise Previous Questions Chapter 4 Principle of Mathematical Induction

Plus One Maths Principle of Mathematical Induction 3 Marks Important Questions

Question 1.
Consider the statement “p(n): 9ⁿ – 1 is a multiple of 8 ”. Where n is a natural number. (MARCH-2011)
i) is p true?
ii) Assuming p(k) is true, Show that p(k+1) is true.
Answer:

Question 2.
Consider the statement “ P(n): xⁿ – yⁿ is divisible by x – y” (MAY-2017)
i) Show that P is true.
ii) Using the principle of Mathematical induction verify that P(n) is true for all natural numbers.
Answer:

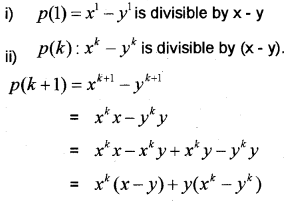
Hence divisible by (x – y).
Therefore by using the principle of mathematical induction true for all n ∈ N .

Plus One Maths Principle of Mathematical Induction 4 Marks Important Questions

Question 1.
Consider the statement “ 7ⁿ – 3ⁿ is divisible by 4” (MARCH-2010)
i) Verify the result for n = 2.
ii) Prove the statement using mathematical induction.
Answer:


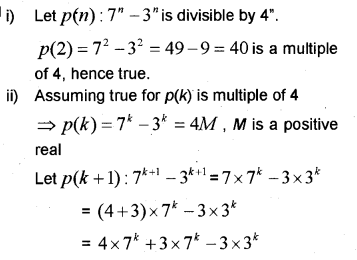
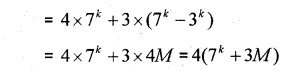
Therefore p(k +1) is multiple of 4. Hence p(n) is true for all natural number n.

Question 2.
i) Which among the following is the least number that will divide 7²ⁿ-4²ⁿ for every positive integer n? [4,7,11,13] (IMP-2010)
ii) Prove by mathematical induction.
(cos θ + i sin θ)ⁿ = (cosnθ + i sin nθ)
Answer:

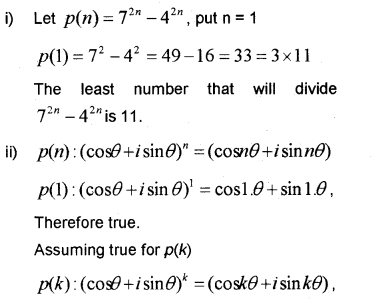
Therefore true for p(k +1). Hence p(n) is true for all natural number n.

Question 3.
Given P(n): 3²ⁿ -1 is divisible by 8. (IMP-2011)
i) Check whether P(1) is true.
ii) If P(k) is true then prove P(k+1) is true.
iii) Is the statement P(n) true for all natural numbers? Justify your answer.
Answer:
i) P(1):3²⁽¹⁾ = 9 -1 = 8 divisible by 8, hence true.
ii) P(k) : 3^2k -1 is divisible by 8.
3^2k– 1 = 8M .
M is a positive real
P(k + 1):3^2k+1 – 1= 3^2k+2 – 1
= 3^2k3² – 1
= 3^2k x 9 – 1
=3^2k x 9 – 9 + 8
= 9(3^2k – 1) + 8
= 9(8M) + 8
Hence divisible by 8
iii) By PMI; true for all natural number n.

Question 4.
Prove that by 1.2 +2.3 + 3.4 + + n(n +1) = \(\frac{n(n+1)(n+2)}{3}\) by using the principle of mathematical induction for all n∈N. (IMP-2012)
Answer:

Hence by using the principle of mathematical induction true for all n∈N .

Question 5.
By the principle of Mathematical Induction, Prove that (IMP-2012)

Answer:


Hence by using the principle of mathematical induction true for all n∈N .

Question 6.
Consider the statement P(n): n(n+1)(2n+1) is divisible by 6 (MARCH-2012)
i) Verify the statement for n = 2.
ii) By assume that P(k) is true for a natural number k, verify that P(k+1) is true.
Answer:
P : 2(2 + 1)(2 x 2 + 1) = 2 x 3 x 5 = 30
Which is divisible by 6.
ii) Assuming that true for p(k)
p(k): k(k +1)(2k +1) is divisible by 6.
k(k +1)(2k +1) = 6M, M is a positive real
Let p(k +1): (k +1)(k + 2)(2(k +1) +1)
= (k + 1)(k + 2)(2k + 3)
= {k + 1){2k² +7k + 6)}
= {(k + 1){(2k²+k) + (6k + 6)}
= k(k + 1)(2k +1) + 6(k + 1)(k +1)
= 6M + 6(k + 1)(k +1)
Hence divisible by 6. Therefore by using the principle of mathematical induction true for all n∈N .

Question 7.
Consider the statement (MARCH-2013)

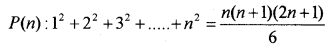
i) Check whether P is true.
ii) By assume that P(k) is true, prove that P(k+1) is true.
iii) Is P(n) true for all natural number n?
justify your answer.
Answer:


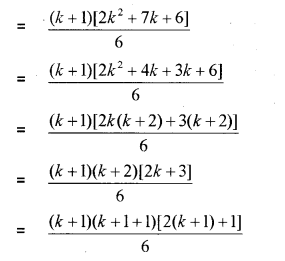
iii) Hence by using the principle of mathematical induction true for all n∈ N .

Question 8.
Consider the statement (MARCH-2013)

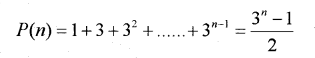
i) Check whether P is true.
ii) If P(k)is true, prove thatP(k+1) is true.
iii) Is P(n) true for all natural number n?
Justify your answer.
Answer:


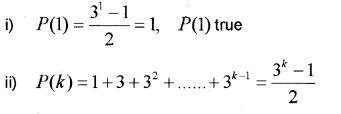
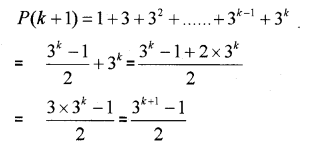
iii) By PMI; true for all natural number n.

Question 9.
Consider the statement (IMP-2014)

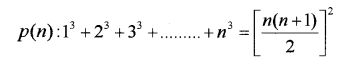
i) Verify the result for n = 2.
ii) Prove the statement using mathematical induction.
Answer:

Hence by using the principle of mathematical induction true for all n∈ N

Question 10.
Consider the statement (MARCH-2014)
P(n) : 1.2 + 2.3 + 3.4 +……… + n(n +1) = \(\frac{n(n+1)(n+2)}{3}\)
i) Prove that P is true.
ii) Assume that P(k) is true for a natural number k, verify that P(k+1) is true.
Answer:

Therefore p(k+1) is true.

Question 11.
Consider the statement (MARCH-2014)
P{n) = 3²ⁿ⁺² – 8n – 9 is divisible by 8
i) Verify the statement for n = 1.
ii) Prove the statement using the principle of mathematical induction for all natural numbers.
Answer:
i) P(1) = 3²⁺² – 8 – 9 = 64 is divisible by 8 . hence true
ii) Assuming true for P(k) is divisible by 8
P(k) = 3^2k+2 – 8k – 9=8M,
M is a positive real
Let P(k +1) = 3^2(k+1)+2 – 8(k) – 9
3^2k+2+2 – 8k – 8 – 9
3^2k+2 x 3² – 8k – 17
= (8M + 8k + 9)9 – 8k – 17
= 72M + 12k + 81 – 8k – 17
= 72M + 64k + 64 = 8(9M + 8k + 8)
Therefore p(k +1) is divisible by 8. Hence p(n) is true for all natural number n.

Question 12.
Consider the statement:(IMP-2014)

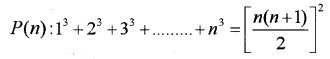
i) Prove that P is true.
ii) If P(k) is true, Prove that P(k+1) is true
iii) Is P(n) true for all natural number n? Why?
Answer:
11 i,ii

Question 13.
Using the principal of mathematical induction, prove that

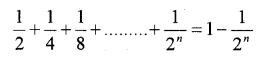
Answer:

It is true.
Therefore P(k+1) is true when ever P(k) is true. By PMI P(n) is true for all n.

Question 14.
A statement p(n) for a natural number n is given by (MARCH-2015)

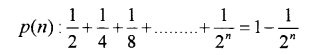
i) Verify that p(1) is true.
ii) By assuming that p(k) is true for a natural number k, show that p(k+1) is true.
Answer:

Question 15.
Consider the statement (IMP-2015)
P(n): 7ⁿ-3ⁿ is divisible by 4.
i) Show that P(1) is true.
ii) Verify, by the method of Mathematical induction, that P (n) is true for all natural numbers.
Answer:

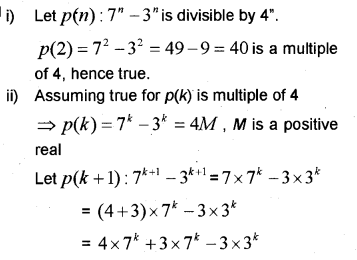
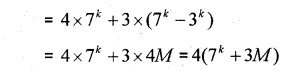
Question 16.
Consider the following statement:

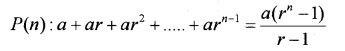
i) Prove that P is true.
ii) Hence by using the principle of mathematical induction, prove that P(n) is true for all natural numbers n. (MARCH-2016)
Answer:

Hence by PMI the result is true for all natural numbers.

Question 17.
Consider the statement “10^2n-1+1 is divisible by 11” verify that P is true and prove the statement by using Mathematical induction.
(MARCH-2017)
Answer:
p(1): 10¹ + 1 = 11 divisible by 11, hence true. Assuming that true for p(k)
p(k): 10^{2k – 1} + 1 is divisible by 11.
10^{2k – 1} + 1 = 11M
p(k + 1):10^{2(k+1) – 1} + 1
= 1o^{2k + 2 – 1} +1
=10^{2k – 1} x 10² + 1
= 10^{2k – 1} x 100 + 1
(11M – 1)100 + 1
= 1100M – 100+1
= 1100M – 99
= 11(100M – 9)
Hence p(k+1)divisible by 11. Therefore by using the principle of mathematical induction true for all n ∈ N .

Plus One Maths Chapter Wise Previous Questions and Answer