Kerala Plus One Economics Chapter Wise Questions and Answers Chapter 17 Correlation
Plus One Economics Correlation One Mark Questions and Answers
Question 1.
Who developed rank correlation co-efficient.
(i) Karl Pearson
(ii) Karl Marx
(iii) Spearman
(iv) None of the above
Answer:
(iii) Spearman
Question 2.
If r= +1, if shows:
(i) Positive correlation
(ii) Perfect positive correlation
(iii) No correlation
(iv) Rank correlation
Answer:
(ii) Perfect positive correlation
Question 3.
If ‘r’ is positive the two variables will more in
(i) Opposite direction
(ii) Inverse direction
(iii) Same direction
(iv) None of the above
Answer:
(iii) Same direction
Question 4.
Which of the following correlation can be used to measure numerically only linear relationships between two variables?
(i) Karl Pearsons coefficient of correlation
(ii) Spearman correlation
(iii) Rank correlation
(iv) None of the above
Answer:
(i) Karl Pearsons coefficient of correlation
Question 5.
The unit of correlation coefficient between height in feet and weight in kgs is
(i) kg/feet
(ii) percentage
(iii) non-existent
Answer:
(iii) non-existent
Question 6.
The range of simple correlation coefficient is
(i) 0 to infinity
(ii) minus one to plus one
(iii) minus infinity to infinity
Answer:
(ii) minus one to plus one
Question 7.
If rxy is positive the relation between X and Y is of the type.
(i) When Y increases X increases
(ii) When Y decreases X increases
(iii) When Y increases X does not change
Answer:
(i) When Y increases X increases
Question 8.
If rxy = 0 the variable X and Y are
(i) linearly related
(ii) not linearly related
(iii) independent
Answer:
(ii) not linearly related
Question 9.
Of the following three measures which can measure any type of relationship
(i) Karl Pearson’s coefficient of correlation
(ii) Spearman’s rank correlation
(iii) Scatter diagram
Answer:
(iii) Scatter diagram
Question 10.
If precisely measured data are available the simple correlation coefficient is
(i) more accurate than rank correlation coefficient
(ii) less accurate than rank correlation coefficient
(iii) as accurate as the rank correlation coefficient
Answer:
(iii) as accurate as the rank correlation coefficient
Question 11.
Define correlation.
Answer:
Correlation studies and measures the direction and intensity of relationship among variables.
Question 12.
Write the formula for calculating correlation.
Answer:
1. Karl Pearson’s coefficient of correlation
\(r=\frac{\sum x y}{\sqrt{\sum x^{2} \times \sum y^{2}}}\)
2. Spearman’s Rank correlation coefficient
\(R=1-\frac{6 \Sigma D^{2}}{N\left(N^{2}-1\right)}\)
Plus One Economics Correlation Two Mark Questions and Answers
Question 1.
Can r lie outside the -1 and 1 range depending on the type of data?
Answer:
No, r cannot lie outside -1 and 1 range depending on the types of data. It lies between minus one and plus one.
Question 2.
Indicate the kind of relationship between X and Y, if the points of the scatter diagram tend to cluster about.
- A straight line sloping upward.
- A straight line sloping downward.
Answer:
- A straight line sloping upward: it is the case of positive correlation.
- A straight line sloping downward: it is the case of negative correlation.
Question 3.
Name the correlation mentioned in the graph.

Answer:
(a) Positive correlation
(b) Negative correlation
(c) No correlation
(d) Perfect positive correlation
(e) Perfect negative correlation
Question 4.
Give two examples each for positive and negative correlation.
Answer:
1. Positive Correlation
- Relation between price and supply
- Relation between height and weight
2. Negative Correlation
- Relation between price and demand
- Sale of woolen garment and day temperature
Question 5.
What are perfect correlations? Give examples.
Answer:
Perfect correlation is that where changes in two related variables are exactly proportional. It is of two types:
a) Positive perfect correlation and
b) Negative perfect correlation
There is perfect positive correlation between the two variables of equal proportional changes are in the same direction. It is expressed as +1. If equal proportional changes are in the reverse direction. Then there is negative perfect correlation and it is described as -1.

Question 6.
Show in scatter diagram the following.
- Positive correlation
- Negative correlation
Answer:

Plus One Economics Correlation Three Mark Questions and Answers
Question 1.
Interpret the values for as 1, -1 and 0.
r=1 r = -1 r = 0
Answer:
r as 1 means that there is perfect positive relationship between two variables r as -1 means that there is perfect negative relationship between two variables r as 0 means that there lack correlation between two variables
Question 2.
List some variables where accurate measurement is difficult.
Answer:
The following are some variables where accurate measurement is difficult.
- Secularism
- Honesty
- Beauty
- Impartiality
- Patriotism
Question 3.
State the nature of relationship.
- sale of woolen garments and the day temperature
- amount of rainfall and yield of crop
- the colour of dress and intelligence of the lady
Answer:
- negative correlation
- positive correlation
- no correlation
Question 4.
Write down the merits of scatter diagram.
Answer:
Merits of scatter diagram are pointed out below:
- It is a very simple method of studying correlation.
- Just a glance of the diagram will show the relationship.
- It indicates whether the relationship is positive or negative.
Question 5.
Construct a flow chart showing the methods of measuring correlation?
Answer:

Question 6.
Illustrate positive correlation and negative correlation.
Answer:
Correlation is commonly classified into negative and positive correlation.
The correlation is said to be positive when the variables move together in the same direction. When the income rises, consumption also rises. When income falls, consumption also falls. For instance, sale of ice-cream and temperature move in the same direction.
The correlation is negative when they move in opposite directions. When the price of apples falls its demand increases. When the prices rise its demand decreases. When you spend more time in studying, chances of your failing decline. These are instances of negative correlation. The variables move in opposite direction.
Question 7.
Calculate the coefficient of correlation from the following data.
![]()
Answer:

Question 8.
The following are the ranks obtained by 10 students in two subjects. Calculate Spearman’s rank correlation.
| Rank of Statistics | Rank of Economics |
| 1 | 2 |
| 2 | 4 |
| 3 | 1 |
| 4 | 5 |
| 5 | 3 |
| 6 | 9 |
| 7 | 7 |
| 8 | 10 |
| 9 | 6 |
| 10 | 8 |
Answer:

Question 9.
Calculate coefficient of correlation using the following data.
![]()
Answer:

Plus One Economics Correlation Five Mark Questions and Answers
Question 1.
What do you mean by Spearman’s rank correlation coefficient? Point out the situations where it is used. Also, bring about its usefulness.
Answer:
Spearman’s rank correlation was developed by the British psychologist C.E. Spearman. It is used when the variables cannot be measured meaningfully as in the case of price, income, weight, etc. The ranking may be more meaningful when the measurements of the variables are suspect.
There are also situations when you are required to quantify qualities such as fairness, honesty, etc. Ranking may be a better alternative to the quantification of qualities. Moreover, sometimes the correlation coefficient between two variables with extreme values may be quite different from the coefficient without the extreme values. Under these circumstances, rank correlation provides a better alternative to simple correlation.
Rank correlation coefficient and simple correlation coefficient have the same interpretation. Its formula has been derived from simple correlation coefficient where individual values have been replaced by ranks. These ranks are used for the calculation of correlation. This coefficient provides a measure of linear association between ranks assigned to these units, not their values. It is the Product Moment Correlation between the ranks.
Question 2.
“Correlation Coefficient has certain essential properties”-substantiate.
Answer:
Correlation Coefficient has certain essential properties as discussed below.
1. r has no unit. It is a pure number. It means units of measurement are not part of r. r between height in feet and weight in kilograms, for instance, is 0.7.
2. A negative value of /-indicates an inverse relation. A change in one variable is associated with change in the other variable in the opposite direction. When price of a commodity rises, its demand falls. When the rate of interest rises the demand for funds also falls. It is because now funds have become costlier.
3. If r is positive the two variables move in the same direction. If/”= 0 the two variables are uncorrelated. There is no linear relation between them. However other types of relationships may be there.
4. If r = 1 or r = -1 the correlation is perfect. The relation between them is exact.
5. A high value of r indicates strong linear relationship. Its value is said to be high when it is close to+1 or-1.
6. A low value of r indicates a weak linear relation. Its value is said to be low when it is dose to zero.
7. The value of the correlation coefficient lies between minus one and plus one, -1 < r < +1. If, in any exercise, the value of r \s outside this range indicates error in calculation.
8. The value of r is unaffected by the change of origin and change of scale. Given two variables X and Y let us define two new variables.
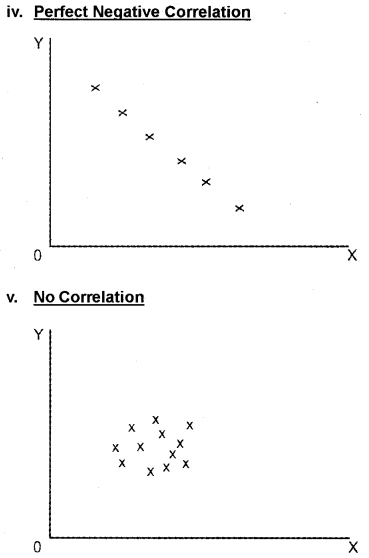
Question 3.
Illustrate the following ideas in scatter diagrams.
i. Positive correlation
ii. Perfect positive correlation
iii. Negative correlation
iv. Perfect negative correlation No correlation
Answer: