Pair Of Linear Equations In Two Variables

Pair Of Linear Equations In Two Variables

A statement of equality of two algebraic expressions, which involve one or more unknown quantities is known as an equation. If there are two unknown quantities then equation is called linear equation in two variables.
A linear equation is an equation which involves linear polynomials.
A value of the variable which makes the two sides of the equation equal is called the solution of the equation.
Same quantity can be added/subtracted to/from both the sides of an equation without changing the equality.
Both the sides of an equation can be multiplied/divided by the same non-zero number without changing the equality.
Note :- To find value of variables in any equation we required number of equation equal to number of variables in equation.

General Form Of Pair Of Linear Equation

a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0
where a₁, b₁, c₁ & a₂, b₂, c₂ are constants.

Graph Of Linear Equation ax + by + c = 0 in Two Variables, where a ≠ 0, b ≠ 0

Step I: Obtain the linear equation, let the equation be ax + by + c = 0.
Step II: Express y in terms of x to obtain \(y=-\left( \frac{ax+c}{b} \right)\)
Step III: Give any two values to x and calculate the corresponding values of y from the expression in step II to obtain two solutions, say (α₁, β₁) and (α₂, β₂). If possible take values of x as integers in such a manner that the corresponding values of y are also integers.
Step IV: Plot points (α₁, β₁) and (α₂, β₂) on a graph paper.
Step V: Join the points marked in step IV to obtain a line. The line obtained is the graph of the equation ax + by + c = 0.

Graph Of Linear Equation ax + by + c = 0 in Two Variables Example Problems With Solutions

https://www.youtube.com/watch?v=DWj-aRuMaJU

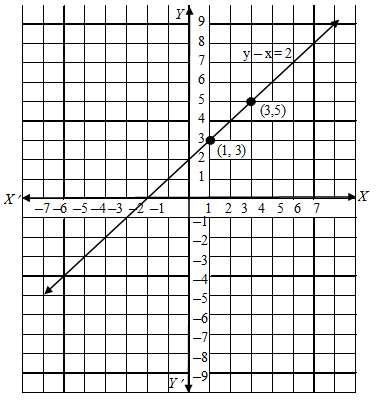
Example 1:    Draw the graph of the equation y – x = 2.
Solution:    We have,
y – x = 2
⇒  y = x + 2
When x = 1,     y = 1 + 2 = 3
When x = 3,    y = 3 + 2 = 5
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation.
Plotting the points (1, 3) and (3, 5) on the graph paper and drawing a line joining them, we obtain the graph of the line represented by the given equation as shown in Fig.

Example 2:    Draw a graph of the line x – 2y = 3. From the graph, find the coordinates of the point when (i) x = – 5   (ii) y = 0.
Solution:    We have x – 2y = 3
⇒   \(y=\frac { x-3 }{ 2 }\)
When x = 1, y = = –1
When x = –1, y = = –2
Plotting points (1, –1) & (–1, –2) on graph paper & joining them, we get straight line as shown in fig. This line is required graph of equation x – 2y = 3.

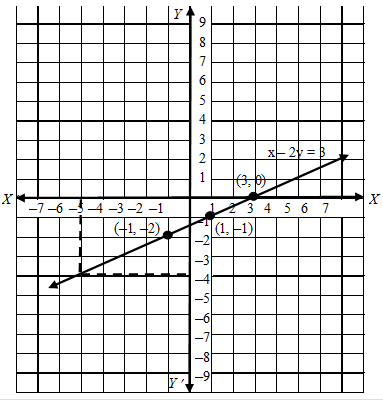
To find the coordinates of the point when x = –5, we draw a line parallel to y-axis and passing through (–5, 0). This line meets the graph of x – 2y = 3 at a point from which we draw a line parallel to x-axis which crosses y-axis at y = –4. So, the coordinates of the required point are (–5, –4).
Since y = 0 on x-axis. So, the required point is the point where the line meets x-axis. From the graph the coordinates of such point are (3, 0).
Hence, required points are (–5, –4) and (3, 0).

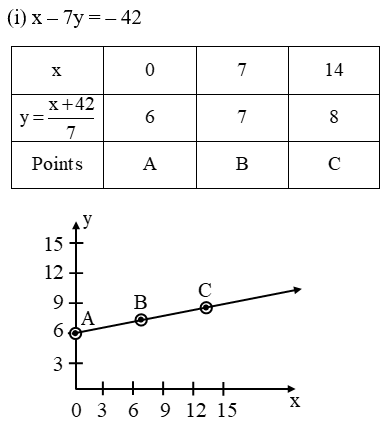
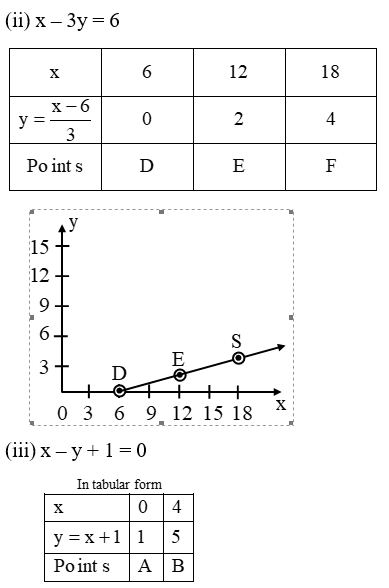
Example 3:    Draw the graph of
(i) x – 7y = – 42
(ii) x – 3y = 6
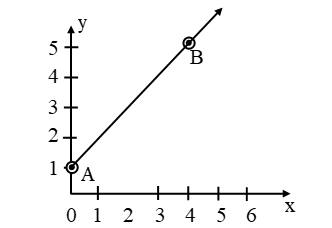
(iii) x – y + 1 = 0
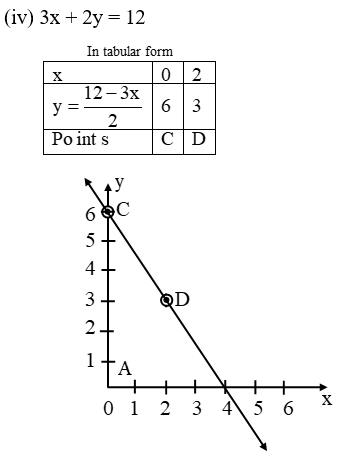
(iv) 3x + 2y = 12
Solution:




Note:
(i) The graph of any linear equation is a line and every solution of equations lies on the graph of that equation.
(ii) If a point (a, b) is not on the line then this point is not a solution of given equation.

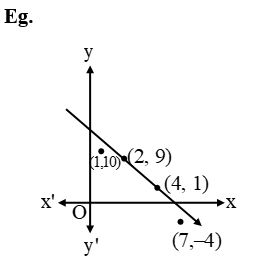
∵ (2, 9) and (4, 1) are on the line
∴ These two points are solution of given equation
But (1, 10) and (7, –4) are not on the line so these two are not solutions.

Example 3:    If  (9/2, 6) is lies on graph of 4x + ky = 12 then find value of k.
Solution:

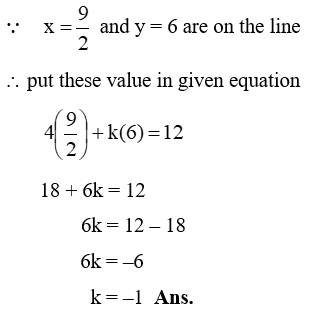
Note:
(1) Equation of x-axis is y = 0 and any point in ordered pair form which is on the x axis is (±a, 0).
(2) Equation of y axis is x = 0 and any point on y axis is (0, ±b)

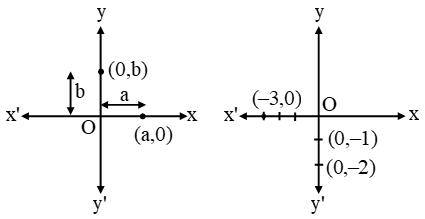
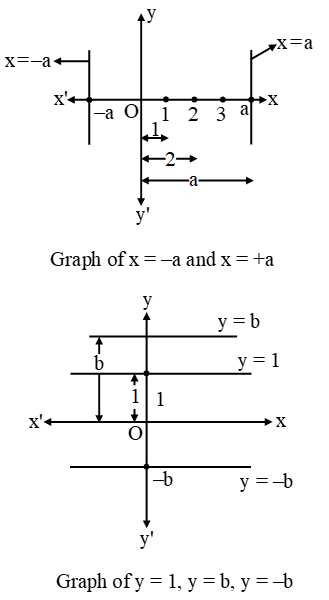
(3) Graph of line x = ±a is parallel to y axis
(4) Graph of line y = ±b is parallel to x axis

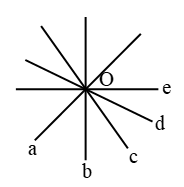
Concurrent lines:
Three or more lines are called concurrent if all lines passes through a common point. These all lines a, b, c, d, e are passes through O.
∴ These are concurrent lines

Note:
From a point there are infinite lines can pass, so we can find (or make) infinite equations of lines which passes through a given point.

Example 4:    Find five equations of lines which passes through (3, –5).
Solution:    x + y = –2, x – y = 8,
2x + y = 1, 2x – y = 11,
2x + 3y + 9 = 0