Newton’s Law Of Universal Gravitation
Any two particles in the universe attract each other. This force is called the force of gravitation.
This concept was given by Newton.
According to newton, “Any two bodies in universe attract each other with a force directly proportional to the product of their masses and inversely proportional to the square of the distance between them.”
Mathematical expression:
Lat A and B be two particle of mass m1 and m2 respectively. Let the distance AB = r.
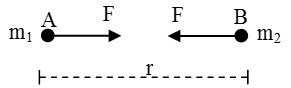
By the law of gravitational, the particle A attracts the particle B with a force F such that
F ∝ m1m2 (for a given pair of particles)
\( \text{F}\propto \frac{\text{1}}{{{\text{r}}^{\text{2}}}}\text{ }\left( \text{for a given separation between the particles} \right) \)
\( \text{So F}\propto \frac{{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}{{{\text{r}}^{\text{2}}}} \)
\( \text{or F}=\text{G}\frac{{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}{{{\text{r}}^{\text{2}}}} \)
Here G is a constant known as the universal constant of gravitation. G = 6.67 × 10-11 Nm2/kg2
G is independent of the masses of the bodies and the distance between them.
Newton’s law of gravitation is applicable for everybody in the universe.
Note: The force between any two bodies in the universe is called the force of gravitation while the force with which earth attracts a body is called the force of gravity.
Some Scientific Phenomenon Based on Gravitational Force:
- The gravitational force between the sun and the earth keeps the earth moving around the sun.
- The gravitational force b/w the earth and the moon keeps the moon moving around the earth.
Existence of our solar system is due to gravitational force. - Gravitation force of the sun and the moon on the earth’s water surface is responsible for the tides in sea.
- Atmosphere above the earth is held due to gravitational force of the earth.
- Gravitational force between the sun and planet keeps the planet moving around the sun.
- Gravitational force is responsible for providing the centripetal force required by the planets.
- The attractive force of the earth is responsible for providing the centripetal force required by moon.
Newton’s Third Law of Motion and Law of Gravitation:
- Newton’s third law of motion is applicable to gravitation also.
Example: If the earth exerts a force of attraction on a body, the body also exerts an equal and opposite force of attraction on the earth. - As a = F/m
mass of the body is larger, acceleration produced will be smaller and vice versa.
Newton’s Law Of Gravitation Example Problems With Solutions
Example 1: Calculate the force between two masses of 100 kg and 1000 kg separated by a distance of 10 m (G = 6.67 × 10-11 Nm2/kg2).
Solution: According to Newton’s law of gravitation, force of attraction between two bodies is
\(F=\text{G}\frac{{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}{{{\text{r}}^{\text{2}}}} \)
Here, m1 = 100 kg; m2 = 1000 kg;
r = 10 m; G = 6.67 × 10-11 Nm2/kg2
\(\therefore F=\frac{6.67\times {{10}^{-11}}\times 100\times 1000}{{{(10)}^{2}}}\)
= 6.67 × 10-8 N
Example 2: Given mass of earth = 6 × 1024 kg, radius of earth = 6.4 × 106 m. Calculate the force of attraction experienced by a man of mass 50 kg.
Solution: Force of gravitation is given by the expression,
\(F=\text{G}\frac{{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}{{{\text{r}}^{\text{2}}}} \)
Here, mass of earth, m1 = 6 × 1024 kg;
mass of man, m2 = 50 kg
Distance between them is to be taken equal to the radius of earth.
∴ r = 6.4 × 106 m
Substituting these values, we get
\(\text{F}=\frac{6.67\times {{10}^{-11}}\times 6\times {{10}^{24}}\times 50}{{{(6.4\times {{10}^{6}})}^{2}}}\)
F = 488.5 N
Example 3: Compare the gravitational forces exerted by the sun and the moon on earth. Which exerts a greater force on earth ?
(Given: mass of sun, Ms = 4 × 1031 kg; mass of moon, Mm = 6.3 × 1022 kg; distance between sun and earth, rse = 1.3 × 1012 m and the distance between moon and earth, rme = 4.5 × 108m)
Solution: If mass of sun is Ms and mass of earth is Me and distance between the sun and earth is rse, then force exerted by the sun on earth is
\( {{F}_{s}}=\frac{G{{M}_{s}}{{M}_{e}}}{{{({{r}_{se}})}^{2}}}\text{ }….\text{(1)} \)
Similarly, if mass of moon is Mm, mass of earth is Me, the distance between moon and earth is rme, then force exerted by moon on the earth is
\( {{F}_{m}}=\frac{G{{M}_{m}}{{M}_{e}}}{{{({{r}_{me}})}^{2}}}\text{ }….\text{(2)} \)
Dividing equation (1) by equation (2), we get
\( \frac{{{F}_{s}}}{{{F}_{m}}}=\frac{G{{M}_{s}}{{M}_{e}}}{{{({{r}_{se}})}^{2}}}\times \frac{r_{me}^{2}}{G{{M}_{m}}{{M}_{e}}} \)
\( =\frac{{{M}_{s}}}{{{M}_{m}}}\times \frac{{{({{r}_{me}})}^{2}}}{{{({{r}_{se}})}^{2}}} \)
\( =\frac{4\times {{10}^{31}}}{6.3\times {{10}^{22}}}\times {{\left( \frac{4.5\times {{10}^{8}}}{1.3\times {{10}^{12}}} \right)}^{2}} \)
= 76.07
∴ The force exerted by the sun on earth is about 76 times the force exerted by the moon on earth.
Example 4: If mass and radius of earth is 6.0 × 1024 kg and 6.4 × 106 m respectively, calculate the force exerted by earth on a body of mass 1 kg. Also, calculate
(i) acceleration produced in the body of mass 1 kg, and
(ii) acceleration produced in the earth
Solution: From Newton’s law of gravitation, we know that the force of attraction between two bodies is given by
\(F=\text{G}\frac{{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}{{{\text{r}}^{\text{2}}}} \)
Here, m1 = mass of earth = 6.0 × 1024 kg;
m2 = mass of body = 1 kg
r = distance between the two bodies
= radius of earth = 6.4 × 106 m
G = 6.67 × 10–11 Nm2/kg2
\( \therefore F=\frac{6.67\times {{10}^{-11}}\times 6.0\times \,{{10}^{24}}\times 1}{{{(6.4\times {{10}^{6}})}^{2}}} \)
= 9.8 N
This shows that earth exerts a force of 9.8 N on a body of mass of 1 kg. The body will exert an equal force of attraction of 9.8 N on earth.
(i) Acceleration produced in the body of mass 1kg
Force = mass × acceleration
∴ Acceleration,
\( a=\frac{F}{m}=\frac{9.8}{1}=9.8\text{ }m/{{s}^{2}} \)
Thus, the acceleration produced in a body of mass 1 kg due to attraction of earth is 9.8 m/s2 , which is quite large. Thus, when a body is released, it falls towards the earth with an acceleration of 9.8 m/s2 , which can be easily observed.
(ii) Acceleration produced in the earth
Similarly, acceleration of earth is given by
\( =\frac{\text{Force}\,}{\text{Mass}\,\text{of}\,\text{earth}}=\frac{9.8}{6.0\times {{10}^{24}}} \)
= 1.63 × 10-24 m/s2
This shows that the acceleration produced in the earth by a body of mass 1 kg is 1.63 × 10-24 m/s2 which is very small and cannot be observed.