NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.3 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 8 Introduction to Trigonometry Class 10 NCERT Solutions Ex 8.3.
- Introduction to Trigonometry Class 10 Ex 8.1
- Introduction to Trigonometry Class 10 Ex 8.2
- Introduction to Trigonometry Class 10 Ex 8.4
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 8 |
| Chapter Name | Introduction to Trigonometry |
| Exercise | Ex 8.3 |
| Number of Questions Solved | 7 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.3
NCERT Solutions for Class 10 Maths
Page No : 189
Question 1. Evaluate :
(i) \(\frac { { sin18 }^{ 0 } }{ { cos72 }^{ 0 } } \)
(ii) \(\frac { { tan26 }^{ 0 } }{ { cot64 }^{ 0 } } \)
(iii) cos 48° – sin 42°
(iv) cosec 31° – sec 59°
Solution:
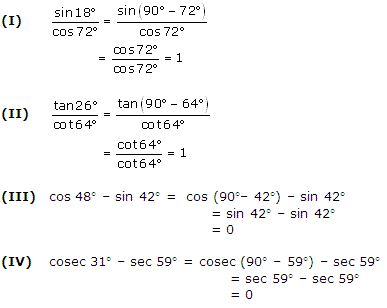
Question 2. Show that :
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:
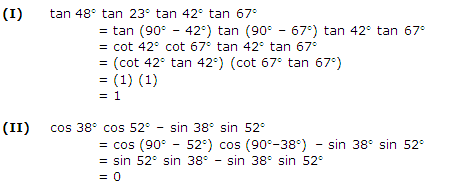
Question 3. If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution:
Given that
tan 2A = cot (A – 180)
cot (900 – 2A) = cot (A -180)
900 – 2A = A – 180
1080 = 3A
A = 360
Question 4. If tan A = cot B, prove that A + B = 90°.
Solution:
Given that
tan A = cot B
tan A = tan (900 – B)
A = 900 – B
A + B = 900
Question 5. If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:
Given that
Sec 4A = cosec (A – 200)
Cosec (900 – 4A) = cosec (A – 200)
900 – 4A = A – 200
1100 = 5A
A = 220
Page No : 190
Question 6. If A, B and C are interior angles of a triangle ABC, then
Show that \(sin\left( \frac { B+C }{ 2 } \right) =cos\frac { A }{ 2 } \)
Solution:
We know that for a triangle ∆ABC
∠A + ∠B + ∠C = 180:
∠B + ∠C = 180 – ∠A
\(\frac { \angle B+\angle C }{ 2 } ={ 90 }^{ 0 }-\frac { \angle A }{ 2 } \)
\(sin\left( \frac { B+C }{ 2 } \right) =sin\left( { 90 }^{ 0 }-\frac { A }{ 2 } \right) \)
\(=cos\left( \frac { A }{ 2 } \right) \)
Question 7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
sin 670 + cos 750
= sin (900 – 230) + cos (900 – 150)
= cos 230 + sin 150
We hope the NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.3 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.3, drop a comment below and we will get back to you at the earliest.