NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 3 Pair of Linear Equations in Two Variables Class 10 NCERT Solutions Ex 3.3.
- Pair of Linear Equations in Two Variables Class 10 Ex 3.1
- Pair of Linear Equations in Two Variables Class 10 Ex 3.2
- Pair of Linear Equations in Two Variables Class 10 Ex 3.4
- Pair of Linear Equations in Two Variables Class 10 Ex 3.5
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 3 |
| Chapter Name | Pair of Linear Equations in Two Variables |
| Exercise | Ex 3.3 |
| Number of Questions Solved | 3 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
Page No: 53
Question 1. Solve the following pair of linear equations by the substitution method.
(i) x + y = 14 ; x – y = 4
(ii) s – t = 3 ; s/3 + t/2 = 6
(iii) 3x – y = 3 ; 9x – 3y = 9
(iv) 0.2x + 0.3y = 1.3 ; 0.4x + 0.5y = 2.3
(v) √2x+ √3y = 0 ; √3x – √8y = 0
(vi) 3/2x – 5/3y = -2 ; x/3 + y/2 = 13/6
Solution:
(i) x + y = 14 … (i)
x – y = 4 … (ii)
From (i), we obtain:
x = 14 – y … (iii)
Substituting this value in equation (ii), we obtain:
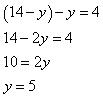
Substituting the value of y in equation (iii), we obtain:
x = 9
∴ x = 9 , y = 5
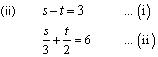
From (i), we obtain:
s = t + 3 …(iii)
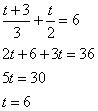
Substituting this value in equation (ii), we obtain:
Substituting the value of t in equation (iii), we obtain:
s = 9
∴ s = 9 , t = 6
(iii) 3x – y = 3 … (i)
9x – 3y = 9 … (ii)
From (i), we obtain
y = 3x – 3 … (iii)
Substituting this value in equation (ii), we obtain:
![]()
9 = 9
This is always true.
Thus, the given pair of equations has infinitely many solutions and the relation between these variables can be given by
y = 3x – 3
So, one of the possible solutions can x = 3, y = 6.


Substituting the value of y in equation (iii), we obtain:
x = 0
∴ x = 0, y = 0

Concept Insight: In order to solve the given pairs of equations, we need to substitute the value of any one of the variable from any one of the equation. But make sure to substitute the value of that variable which simplifies calculations. For example, in part (iv) it is most convenient to substitute the value of x from the first equation to the second equation, as the division by 0.2 is more easier than the division by 0.3, 0.4 and 0.5.
Question 2. Solve 2x + 3y = 11 and 2x – 4y = – 24 and hence find the value of ‘m‘ for which y =mx + 3.
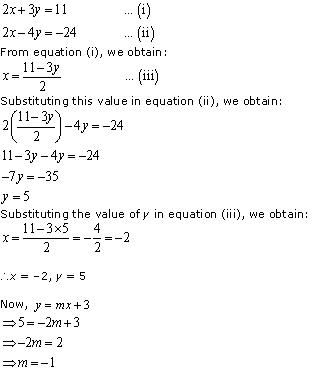
Thus, the value of m is -1.Concept Insight: Firstly the solution of the given pair of linear equations can be found out by substituting the value of one variable, say x, from one equation into the other equation. Then after finding out the values of x and y, substitute them in the equation y = m x + 3 in order to find the value of m.
Question 3. Form the pair of linear equations for the following problems and find their solution by substitution method
(i) The difference between two numbers is 26 and one number is three times the other. Find them.
Solution:
Let one number be x and the other number be y such that y > x.
According to the question:
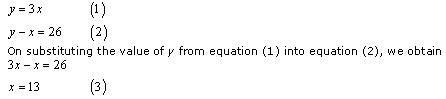
Substituting this in equation (1), we obtain
y = 39
Hence, the numbers are 13 and 39.
Concept Insight: In this problem, two relations between two numbers are given. So, the two numbers have to be found out here. So the two numbers will be represented by variables x and y explicitly state the greater variable.
A pair of equations can be obtained from the given conditions. The pair of equations can then be solved by suitable substitution.
(ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
Solution:
Let the larger angle be x and smaller angle be y.
We know that the sum of the measures of angles of a supplementary pair is always 180º.
According to the given information,
x + y = 180º — (1)
x – y = 180º — (2)
From (1), we obtain
x = 180º – y — (3)
Substituting this in equation (2), we obtain
180º – y – y = 18º
162º = 2y
81º = y —- (4)
Putting this in equation (3), we obtain
x = 180º – 81º
= 99º
Hence, the angles are 99º and 81º.
Concept Insight: This problem talks about the measure of two supplementary angles. So, the two angles will be written as variables. The pair of equations can be formed using the fact that the sum of two supplementary angles is 180° and using the condition given in the problem. The pair of equations can then be solved by suitable substitution.
(iii) The coach of a cricket team buys 7 bats and 6 balls for Rs 3800. Later, she buys 3 bats and 5 balls for Rs 1750. Find the cost of each bat and each ball.
Solution:
Let the cost of a bat and a ball be x and y respectively.
According to the given information,

Hence, the cost of a bat is Rs 500 and that of a ball is Rs 50.
Concept Insight: Cost of bats and balls needs to be found so the cost of a ball and bat will be taken as the variables. Applying the conditions of total cost of bats and balls algebraic equations will be obtained. The pair of equations can then be solved by suitable substitution.
(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is Rs 105 and for a journey of 15 km, the charge paid is Rs 155. What are the fixed charges and the charge per km? How much does a person have to pay for traveling a distance of 25 km?
Solution:

Concept Insight: In this problem, we are required to find out the fixed charge and the charge per km. So, we will represent these two by using different variables. Now, two linear equations can be written by using the conditions given in the problem. The pair of equations can then be solved by suitable substitution.
(v) A fraction becomes 9/11, if 2 is added to both the numerator and the denominator. If, 3 is added to both the numerator and the denominator it becomes 5/6 . Find the fraction.
Solution:
Let the fraction be x/y.
According to the given information,

Concept Insight: This problem talks about a fraction which is not known to us. So numerator and denominators will be taken to be variables x and y respectively and y will be strictly non zero. Then, a pair of linear equations can be formed from the given conditions. The pair of equations can then be solved by suitable substitution.
(vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?
Solution:
Let the age of Jacob be x and the age of his son be y.
According to the given information,

Hence, the present age of Jacob is 40 years whereas the present age of his son is 10 years.
Concept insight: Here, Jacob’s and his son’s present age are not known. So, we will write both these in terms of variables. The problem talks about their ages five years ago and five years hence. Here, five years ago means we have to subtract 5 from their present ages, and five years hence means we have to add 3 to their present ages. So, using the given conditions, a pair of linear equations can be formed. The pair of equations can then be solved by suitable substitution.
We hope the NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3, drop a comment below and we will get back to you at the earliest.