NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.2 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 10 Circles Class 10 NCERT Solutions Ex 10.2.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 10 |
| Chapter Name | Circles |
| Exercise | Ex 10.2 |
| Number of Questions Solved | 13 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.2
NCERT Solutions for Class 10 Maths
Page No: 213
Question 1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5 cm
Solution:

Concept Insight: To answer such type of problems, remember to use the result that the radius is perpendicular to the tangent at the point of contact and then make use of Pythagoras theorem in the right triangle.
Question 2. In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(A) 60° (B) 70° (C) 80° (D) 90°
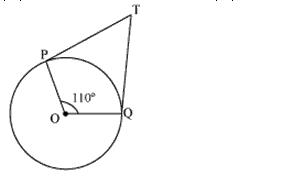
Solution:

Concept Insight: Here, TP and TQ are tangents to the circle and OP and QQ are the radii of the circle. So, here the result, radius is perpendicular to tangent at the point of contact, will be used. Also, remember that the sum of all the interior angles of a quadrilateral is 360°.
Question 3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠ POA is equal to (A) 50° (B) 60° (C) 70° (D) 80°
Solution:


Concept Insight: Here, PA and PB are tangents to the circle and OA and OB are the radii of the circle. So, here the result, radius is perpendicular to tangent at the point of contact, will be used. Also, remember that the sum of all the interior angles of a
quadrilateral is 360°. The key step in this question is to use the congruency of triangles OPB and OPA obtained by joining OP.
Page No: 214
Question 4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:
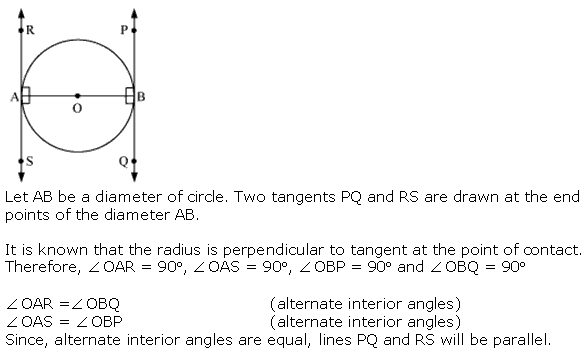
Concept Insight: Here, the result that the radius is perpendicular to tangent at the point of contact, can be used. Then, the criteria of two lines to be parallel will be used here.
Question 5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
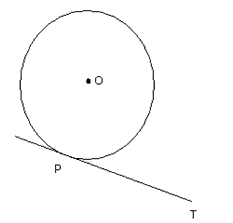
Let P be the point of contact and PT be the tangent at the point P on the circle with centre O,
Since OP is radius of the circle and PT is a tangent at P, OP ⊥ PT.
Thus, the perpendicular at the point of contact to the tangent passes through the centre.
Question 6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution:
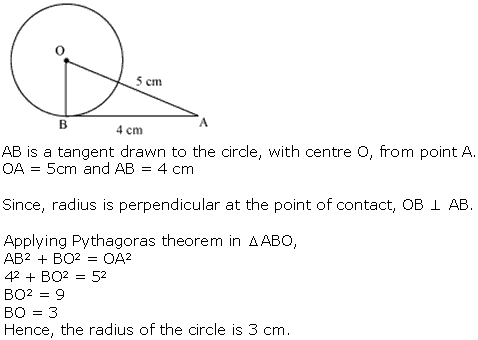
Question 7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the
larger circle which touches the smaller circle.
Solution:

In ∆OPQ, as OA ⊥ PQ, AP = AQ
(Perpendicular from center of circle bisects the chord)
∴ PQ = 2AP =2 x 4 cm = 8 cm
So, length of chord of larger circle is 8cm.
Concept Insight: Here, PQ is a chord of the larger circle and it touches the smaller circle at a point. So, it will act as a tangent to the smaller circle, Then, by applying the result that the radius is perpendicular to the tangent at the point of contact, a right traingle will be obtained in which Pythagoras theorem will be applied. Then, to find the length of the chord PQ, a result can be used, which states that, perpendicular drawn from center of a circle bisects the chord.
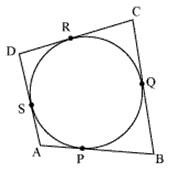
Question 8. A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC.
Solution:
It can be observed that:
DR=DS (tangents from point D)
CR = CQ (tangents from point C)
BP=BQ (tangents from point B)
AP = AS (tangents from point A)
Adding the above four equations,
DR + CR + BP + AP = DS + CQ + BQ + AS
(DR+CR)+(BP+AP)=(DS +AS)+(CQ +BQ)
CD + AB = AD + BC
Concept Insight: AP and AS; BP and BQ; CR and CQ; DR and DS are the pair tangents drawn to the circle drawn from the external points A, B, C, D respectively. So, the result that the tangents drawn from an external point are equal, will be applied here.
Question 9. In Fig. 10.13, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°.
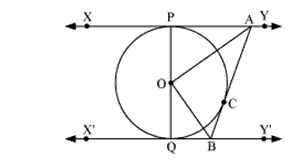
Solution:
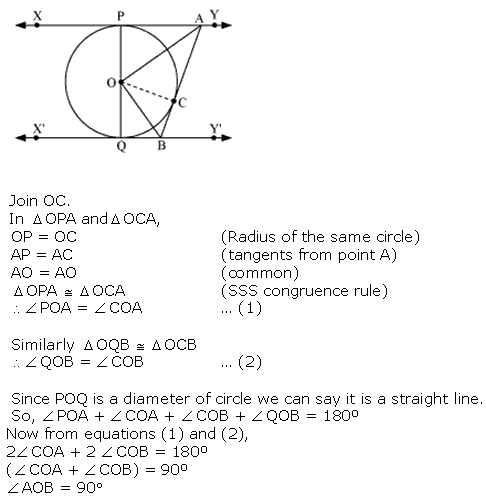
Concept Insight: Here, the key idea is to establish the equality of ∠ POA and ∠ COA by proving the congruency of ∆OPA and ∆OCA and the equality of ∠ QOB and ∠ COB by proving the congruency of ∆OQB and ∆OCB.
Question 10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Solution:

Hence, the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Question 11. Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
Since, ABCD is a parallelogram,
(i) AB = CD
(ii) BC = AD
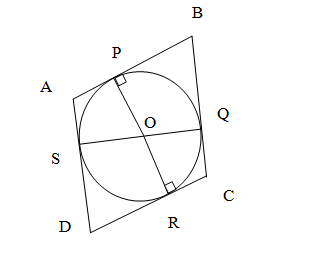
Now, it can be observed that:
DR = DS (tangents on circle from point D)
CR = CQ (tangents on circle from point C)
BP = BQ (tangents on circle from point B)
AP = AS (tangents on circle from point A)
Adding all the above four equations,
DR + CR + BP + AP = DS + CQ + BQ + AS
(DR + CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD + AB = AD + BC
(iii) From equation (i) (ii) and (ii):
2AB = 2BC
AB = BC
AB = BC = CD = DA
Hence, ABCD is a rhombus.
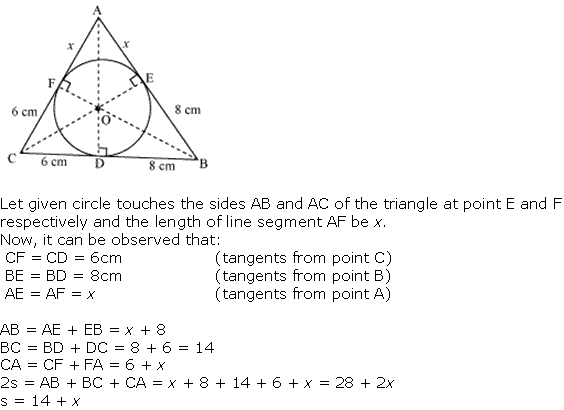
Question 12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
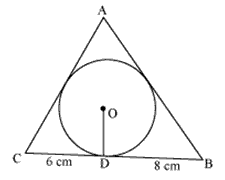
Solution:
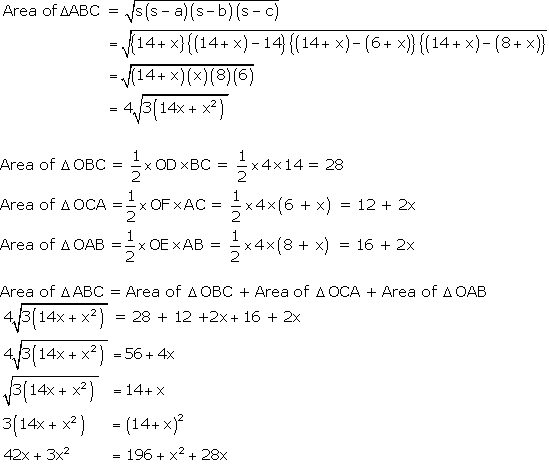

Question 13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:
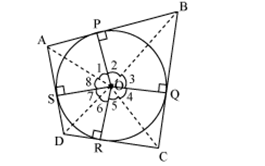


Concept Insight: Here, ¡t ¡s given that a quadrilateral ¡s circumscribing a circle so draw the diagram carefully. From the figure, you can observe pairs of tangents drawn from external points, so the result that tangents from an external point are
equal in length will be applied. Then, the fact that the angle at a point is 3600 will be used.
We hope the NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.2 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 10 Circles Ex 10.2, drop a comment below and we will get back to you at the earliest.