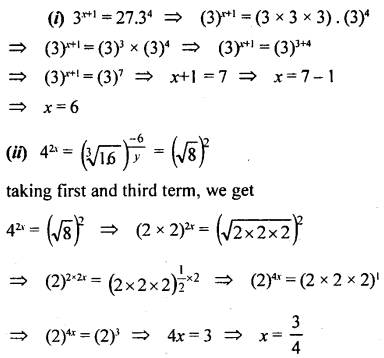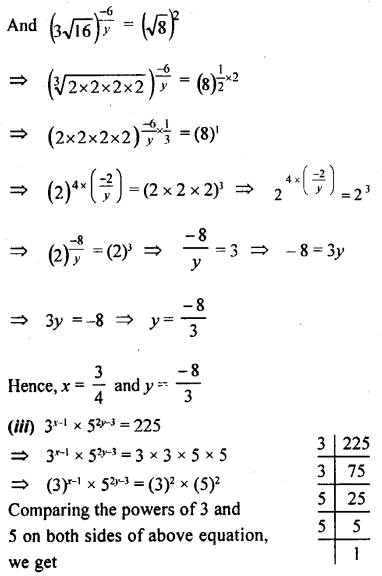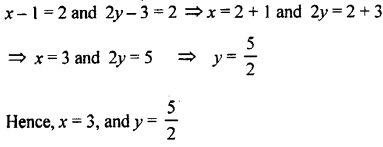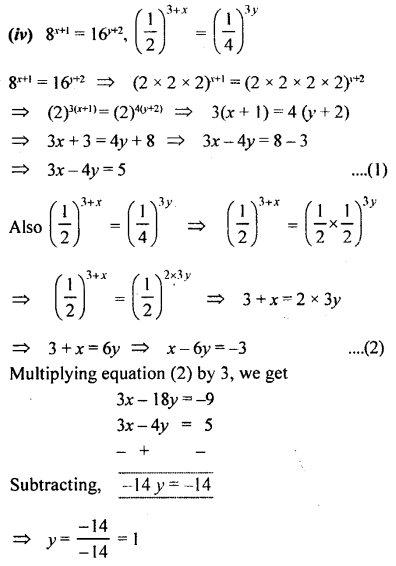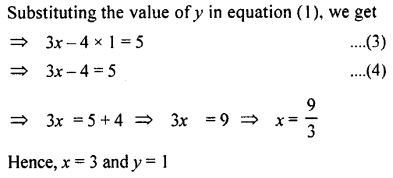ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 8 Indices Chapter Test
Question 1.
If 2x . 3y. 5z = 2160 find the values of x, y and z. Hence compute the value of 3x. 2-y 5-z.
Answer:
2x . 3y. 5z = 2160
=> 2x . 3y. 5z = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 5
=> 2x . 3y. 5z = (2)4.(3)3 . (5)1
Comparing powers of 2, 3 and 5, on both sides of above equation we get
x = 4, y = 3, z = 1
Also 3x. 2-y 5-z = (3)4 × (2)-3 × (5)-1
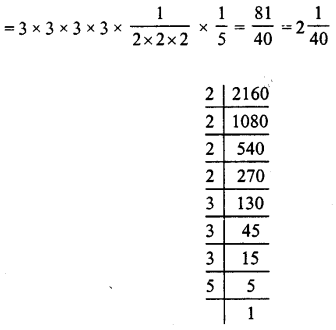
Question 2.
If x = 2 and y = -3, find the values of
(i) xx + yy
(ii) xy + yx.
Answer:
(i) xx + yy, Given that x = 2 and y = 3
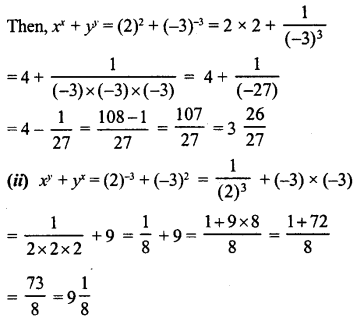
Question 3.
If p = xm+n . yt , q = xn+l. ym and r = xl+m . yn. Prove that pm-n. qn-l . rl-n = 1
Answer:
Given that p = xm+n. yt ………(1)
q = xn+l. ym ….(2)
r = xl+m . yn ..(3)
L.H.S. = pm-n . qn-l . rl-m ……(4)
Putting the value of a, b, c from (1), (2), (3) respectively in (4), we get
L.H.S = (xm+nyt )m-n ,(xn+l ,ym )n-l .(xl+m yn)l-m
= (xm+n)m-n . yl(m-n) . (x)(n+l)(n-l) . ym(n-l). (x)(l+m)(l-m) ym(l-m)
= (x(m+n)(m-n) ylm+ln . (x)(n+l)(n-l) . ymn-l . (x)(l+m)(l-m) . yln+nm
= (x)m2-n2 . ylm-ln . (x)n2-l2 . ymn-ml . (x) l2-m2 . y nl-nm
= (x)m2 – n2 + n2 – l2 + l2 = m2 (y)lm-ln+mn-ml+nl-nm
= (x)o(y)o = 1 × 1 = 1
Hence, Proved L.H.S = R.H.S.
Question 4.
If x = am+n, y = an+1 and z = al+m, prove that xm.ynzl = xn yt zm
Answer:
x = am+n,y = an+l, z = al+m
L.H.S. =xm yn zp
= am[m+n] . yx[n+l] . zl[l+m]
= am2+mn . yn2+nl . zl2+lm
= am2+mn+n2+nl+l2+lm = al2+m2+n2+lm+mn+np
R.H.S. = xn . yl . zm
= an(m+n) . al(n+p) . am(l+m)
= amn+n2 . al(n+p) . am(l+m)
= amn+n2 . aln+l2 . alm+m2
= amn+n2+ln+l2+lm+m2
= al2+m2+n2+lm+mn+nl
∴ L.H.S. = R.H.S.
Question 5.
Show that
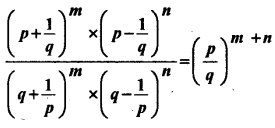
Answer:
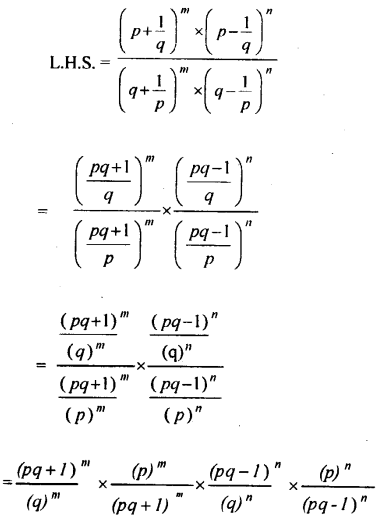
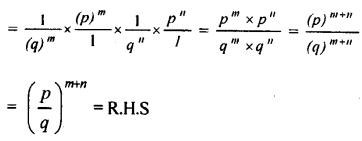
Hence, L.H.S = R.H.S, Proved the result.
Question 6.
If x is a positive real number »nd exponents are rational numbers, then simplify the following :
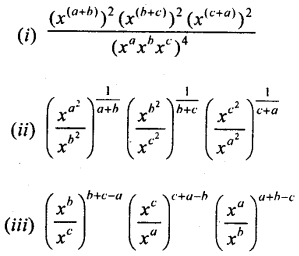
Answer:
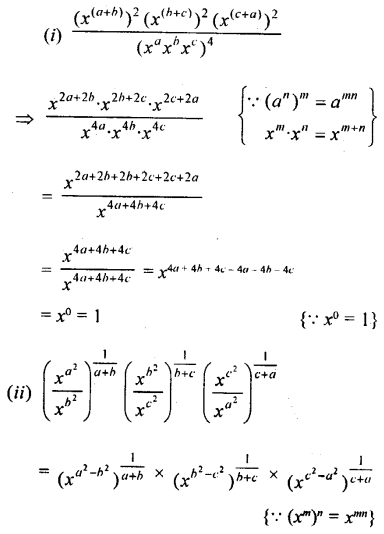
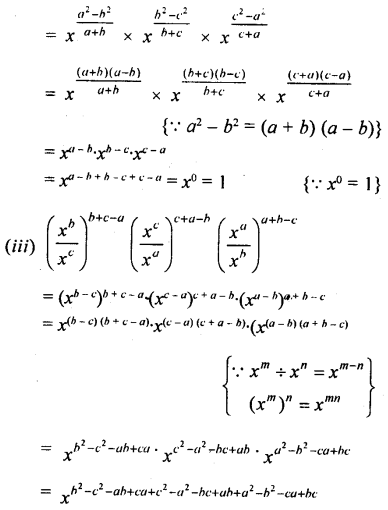

Question 7.
Show that:
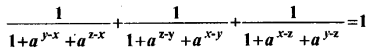
Answer:
L.H.S =

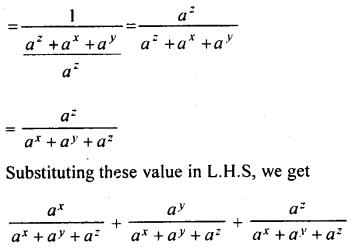
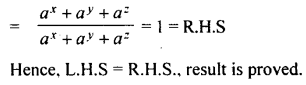
Question 8.
If 3x = 5y = (75)z show that z = \(\frac{x y}{2 x+y}\).
Answer:
Let 3x = 5y = (75)z = k

Question 9.
Solve the following equations:
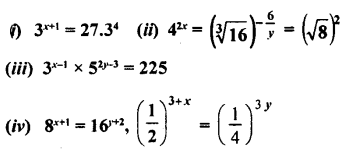
Answer: