ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 19 Coordinate Geometry Chapter Test
Question 1.
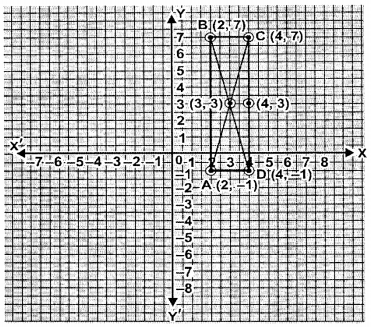
Three vertices of a rectangle are A (2, -1), B (2, 7) and C(4, 7). Plot these points on a graph and hence use it to find the co-ordinates of the fourth vertex D Also find the co-ordinates of
(i) the mid-point of BC
(ii) the mid point of CD
(iii) the point of intersection of the diagonals. What is the area of the rectangle ?
Answer:
Given three vertices of a rectangle are A (2, -1), B (2, 7) and C (4, 7)
From graph the co-ordinates of the fourth vertex D (4, -1)
(i) mid-point of BC is (3, 7)
(ii) mid-point of CD is (4, 3)
(iii) The point of intersection of the diagonals (3, 3). Area of rectangle ABCD = AB × BC = 8 × 2 sq. units = 16 sq. units.
Question 2.
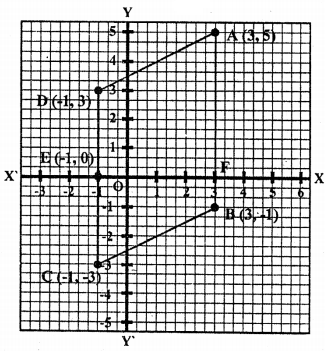
Three vertices of a parallelogram are A (3, 5), B (3, -1) and C (-1, -3). Plot these points on a graph paper and hence use it to find the coordinates of the fourth vertex D. Also find the coordinates of the mid-point of the side CD. Waht is the area of the parallelogram?
Answer:
The vertices A, B and C of parallelogram are A (3, 5), B (3, -1) and C (-1,-3)
D is the fourth vertex of the parallelogram which is (-1, 3)
E is the mid-piont of CD whose coordinates are (-1, 0)
Now area of the parallelogram ABCD
= Base × Height = AB × EF = 6 × 4 = 24 sq. units
Question 3.
Draw the graphs of the following linear equations.
(i) y = 2x – 1
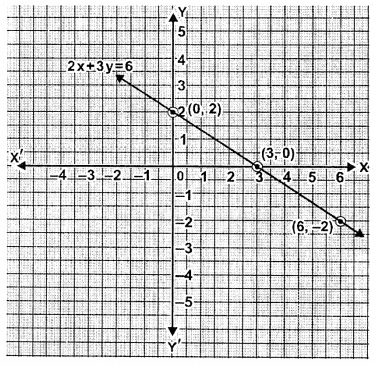
(ii) 2x + 3y = 6
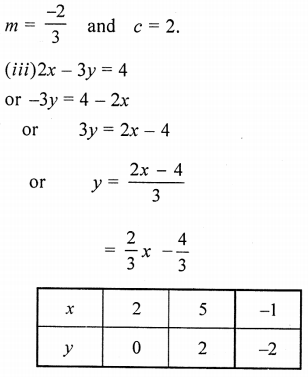
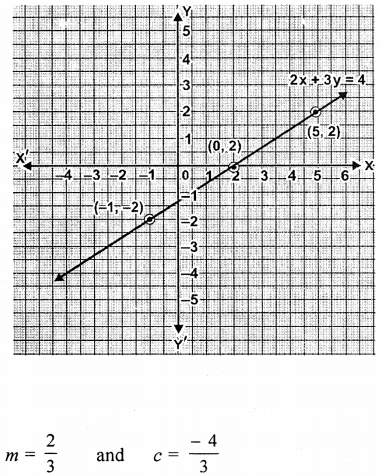
(iii) 2x – 3y – 4.
Also find slope and j-intercept of these lines.
Answer:
(i) y = 2x – 1
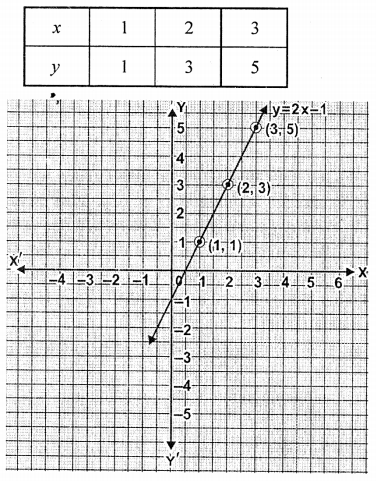
m = 2 and c = -1
(ii) 2x + 3y = 6 or 3y = 6 – 2x
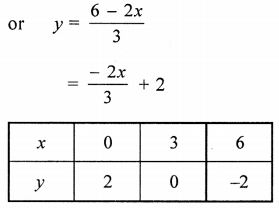
Question 4.
Draw the graph of the equation 3x – 4y = 12. From the graph, find :
(i) the value of y when x = -4
(ii) the value of x when y = 3.
Answer:
Given equation is 3x – 4y = 12

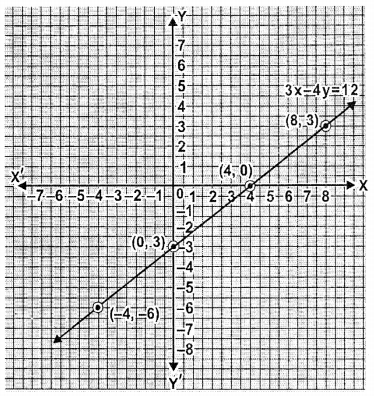
(i) when x = -4 then value of y = -6
(ii) when y = 3 then value of x = 8.
Question 5.
Solve graphically, the simultaneous equations: 2x – 3y = 1; x + 6y = 11.
Solution:
2x – 3y = 7, x + 6y = 11
2x – 3y = 7 ⇒ 2x = 3y + 7
⇒ x = \(\frac{3 y+7}{2}\)
Giving some different value to y, we get corresponding value of x.
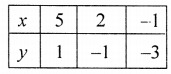
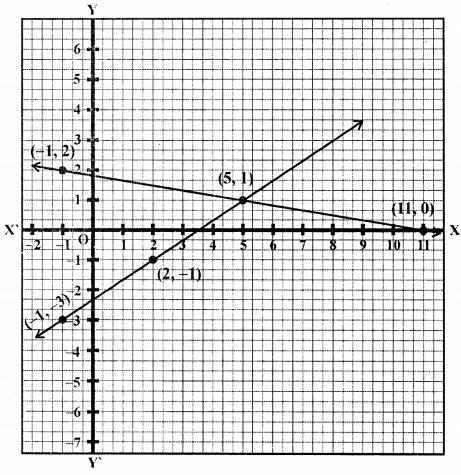
Plot the points (5, 1), (2, -1) and (-1, -3) on the graph and join them to get a line. Similarly in
x + 6y = 11 ⇒ x = 11 – 6y
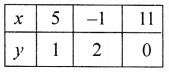
Now plot the points (5, 1), (-1, 2) and (11, 0) and join them to get another line.
We see that there two lines intersect at (5, 1)
Hence x = 5, y = 1
Question 6.
Solve the following system of equations graphically: x – 2y – 4 = 0, 2x + y – 3 = 0.
Solution:
x – 2y – 4 = 0 and 2x + y – 3 = 0
x – 2y – 4 = 0 ⇒ x = 2y + 4
Giving some different value toy, we get corresponding values of x
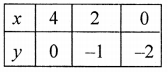
Plot the points (4, 0), (2, -1) and (0, -2) on the graph and join them to get a line.
Similarly in 2x + y – 3 = 0 ⇒ y = 3 – 2x
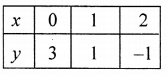
Plot the points (0, 3), (1, 1) and (2, -1) and join them to get another line.
We see that these lines intersect each other at x = 2, y = -1

Question 7.
Using a scale of 1 cm to 1 unit for both the axes, draw the graphs of the following equations : 6p = 5x + 10, y = 5x – 15. From the graph, find
(i) the coordinates of the point where the two lines intersect.
(ii) the area of the triangle between the lines and the x-axis.
Solution:
6y = 5x + 10, y = 5x – 15
6y = 5x + 10 ⇒ y = \(\frac{5 x+10}{6}\)
Giving some different values to x, we get corresponding values of y

Plot the points (1, 2, 5), (-2, 0) and (4, 5) on the graph and join them to get a line.
Similarly in y = 5x – 15
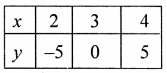
Plot the points (2, -5), (3, 0) and (4, 5) on the graph and join them to get a line.
We see that three two lines intersect each other at
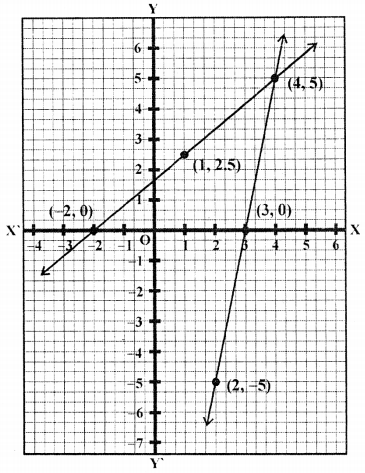
Question 8.
Find, graphically, the coordinates of the vertices of the triangle formed by the lines : 8y – 3x + 7 = 0, 2x – y + 4 = 0 and 5x + 4 y = 29.
Solution:
8y – 3x + 7 = 0 ⇒ 8y = 3x – 7
⇒ y = \(\frac{3 x-7}{8}\)
Giving some different values to x, we get corresponding values of y
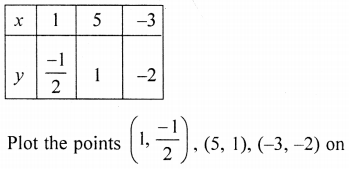
the graph and join them to get a line
2x – xy + 4 = 0 ⇒ 2x = y – 4
⇒ x = \(\frac{y-4}{2}\)
Giving some different values to y, we get corresponding value of x.
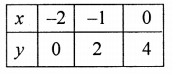
Plot the point on the graph and join them to get a line
and 5x + 4y = 29 ⇒ 5x = 29 – 4y
⇒ x = \(\frac{29-4y}{5}\)
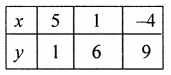
Plot the points on the graph and join them to get another line.
We see that there three lines intersect each other at (-3, -2), (1, 5) and (1, 6) respectively Therefore vertices of (-3, -2, (1, 5), (1, 6).
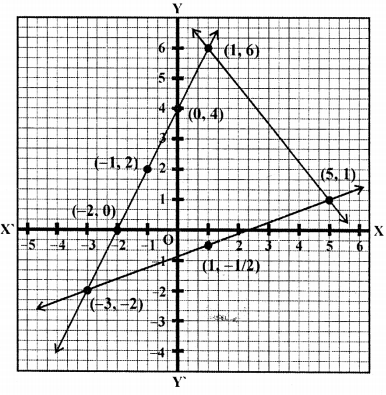
Question 9.
Find graphically the coordinates of the vertices of the triangle formed by the lines y – 2 = 0, 2y + x = 0 and y + 1 = 3(x – 2). Hence, find the area of the triangle formed by these lines.
Solution:
y – 2 = 0
y = 2, which is parallel to x-axis
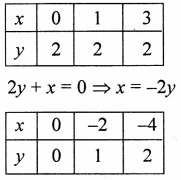
Plot the points (0, 0), (-2, 1) and (-4, 2) on the graph and join them to get a line.
y + 1 = 3(x – 2) = 3x – 6
Giving some different values to x, we get corresponding the value of y
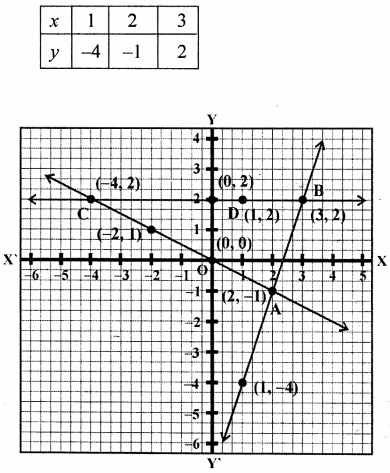
Plot the points (1, -4), (2, -1) and (3, 2) on the graph and join them to get another line. Now we see that three lines intersect each other.
Coordinates of the vertices of the triangle are (2, -1), (3, 2), (-4, 2) and
∴ Area of triangle = \(\frac{\mathrm{BC} \times \mathrm{AB}}{2}\)
= \(\frac{7 \times 3}{2}=\frac{21}{2}\) = 10.5 cm2
Question 10.
A line segment is of length 10 units and one of its end is (-2, 3). If the ordinate of the other end is 9, find the abscissa of the other end.
Solution:
Ordinates of the point on the other end (y) = 9
Let abscissa (x) = x
Then distance between the two ends (-2, 3)

⇒ x2 + 4x + 4 + 36 = 100
⇒ x2 + 4x = 100 – 36 – 4 = 60
⇒ x2 + 4x – 60 = 0
⇒ x2 + 10x – 6x – 60 = 0
⇒ x(x + 10) – 6(x + 10) = 0
⇒ (x+ 10) (x – 6) = 0
Either x + 10 = 0, then x = -10
or x – 6 = 0, then x = 6
∴ Abscissa will be -10 or 6
Question 11.
A (-4, -1), B (-1, 2) and C (α, 5) are the vertices of an isosceles triangle. Find the value of α, given that AB is the unequal side.
Solution:
A (-4, -1), B (-1, 2) and C (a, 5) are vertices of an isosceles triangle. AB is the unequal side.
∴ AC = BC
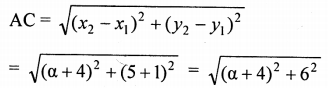
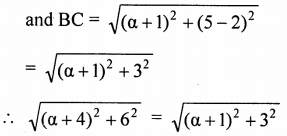
Squaring both sides,
(α + 4)2 + 36 = (α + 1)2 + 9
a2 + 8α + 16 + 36 = α2 + 2α + 1 + 9
8α – 2α = 1 + 9 – 16 – 36
6α = -42 ⇒ α = \(\frac{-42}{6}\) = -7
∴ α = -7
Question 12.
If A (-3, 2), B (α, β) and C (-1, 4) are the vertices of an isosceles triangle, prove that α + β = 1, given AB = BC.
Solution:
A (-3, 2), B (α, β) and C (-1, 4) are the value of an isosceles triangle AB = BC

Squaring both sides,
(α + 3)2 + (β – 2)2 = (α + 1) + (β – 4)2
⇒ α2 + 6α + 9 + β2 – 4β + 4 = α2 + 2α + 1 + β2 – 8β + 16
6α – 2α – 4β + 8β = 16 – 9 – 4 + 1
4α + 4β = 4 ⇒ α + β = 1 (dividing by 4)
Hence α + β = 1
Question 13.
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right angled isosceles triangle.
Solution:
Let points A (3, 0), B (6, 4) and (-1, 3) are the vertices of a right angled.
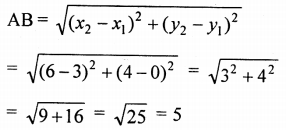
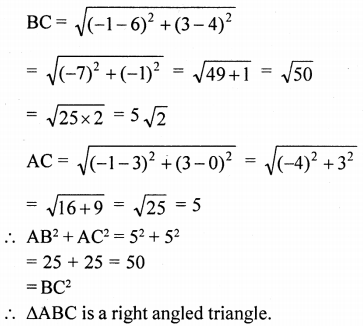
Question 14.
(i) Show that the points (2, 1), (0, 3), (-2, 1) and (0, -1), taken in order, are the vertices of a square. Also find the area of the square.
(ii) Show that the points (-3, 2), (-5, -5), (2, -3) and (4, 4), taken in order, are the vertices of rhombus. Also find its area. Do the given points form a square?
Solution:
(i) Let points A (2, 1), B (0, 3), C (-2, 1) and D (0, -1) taking in order, are the vertices of the square

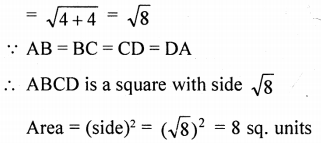
(ii) Let the given points are A (-3, 2), B (-5, -5), C(2, -3) and D (4, 4)
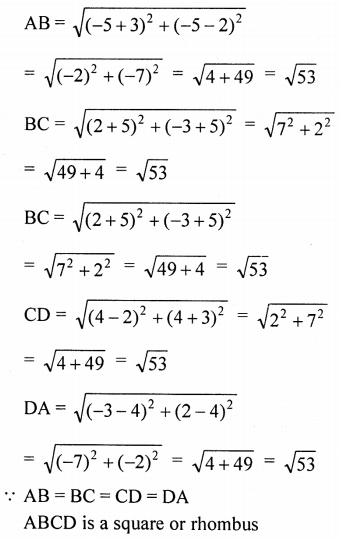

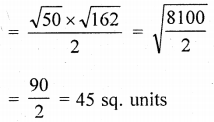
Question 15.
The ends of a diagonal of a square have co-ordinates (-2, p) and (p, 2). Find p if the area of the square is 40 sq. units.
Solution:
Ends of a diagonal of a square are (-2, p) and (p, 2)
Area of square = 40 sq. units
∴ Side = \( \sqrt{{40}} \) units = 2\( \sqrt{{10}} \) units
and diagonal = \( \sqrt{{2}} \) × side
= \( \sqrt{{2}} \) × \( \sqrt{{40}} \) = \( \sqrt{{80}} \) = 4\( \sqrt{{5}} \) unit
Diagonal = AC = \(\sqrt{\left(x_{2}-x_{1}\right)^{2} \times\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(p+2)^{2}+(2-p)^{2}}=4 \sqrt{5}\)
Squaring both side,
(p + 2)2 + (2 – p)2 = 16 × 5 = 80
⇒ p22 + 4p + 4 + 4 – 4p + p2 = 80
⇒ 2p2 + 8 = 80 ⇒ 2p2 = 80 – 8 = 72
⇒ p2 = \(\frac{72}{2}\) = 36 = (±6)2
∴ p = ±6
∴ P = 6, -6
Question 16.
What type of quadrilateral do the points A (2, -2), B (7, 3), C (11, -1) and D (6, -6), taken in the order, form?
Solution:
Vertices of a quadrilateral ABCD are A (2, -2), B (7, 3), C (11, -1), D (6, -6) taken on order.
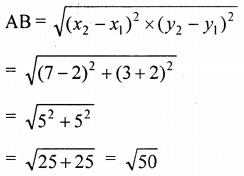

Question 17.
Find the coordinates of the centre of the circle passing through the three given points A (5, 1), B (-3, -7) and C (7, -1).
Solution:
Let coordinates of the centre of the circle be (x, y)
Points A (5, 1), B (-3, -7) and C (7, -1) are on the circle
∴ OA = OB = OC
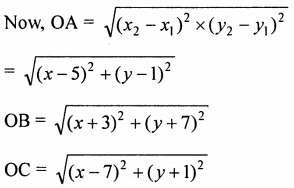
OA2 = OB2 and OA2 = OC2
∴ (x – 5)2 + (y – 1)2 = (x + 3)2 + (y + 7)2
⇒ x2 – 10x + 25 + y2 – 2y + 1 = x2 + 6x + 9 + y2 + 14y + 49
⇒ 6x + 14y+ 10x + 2y = -9 – 49 + 25 + 1
⇒ 16x + 16y = -32
⇒ x + y = -2
⇒ x = -2 – y …(i)
Now OA2 = OC2
(x – 5)2 + (y – 1)2 = (x – 7)2 + (y + 1)2
⇒ x2 – 10x + 25 + y2 – 2y + 1 = x2 – 14x + 49 + y2 + 1 + 2y
⇒ -10x + 14x – 2y – 2y = 49 + 1 – 25 – 1
⇒ 4x – 4y = 24
⇒ x – y = 6 …(ii)
(Taking 4 common)
Now substitute the value of (i) in (ii), we get
⇒ (-2 – y) – y = 6
⇒ -2 – y – y = 6
⇒ -2y = 6 + 2 ⇒ y = \(\frac{-8}{2}\) ⇒ y = -4
Now put the value of y = -4 in equation (i)
x = -2 – 7 = -2 – (-4)
= -2 + 4 = 2
∴ The coordinates of the centre of the circle are (2, -4)