ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 12 Pythagoras Theorem Chapter Test

ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 12 Pythagoras Theorem Chapter Test

Question 1.
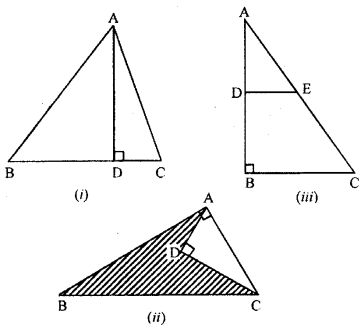
(a) In fig. (i) given below, AD ⊥ BC, AB = 25 cm, AC = 17 cm and AD = 15 cm. Find the length of BC.
(b) In figure (ii) given below, ∠BAC = 90°,
∠ADC = 90°, AD = 6 cm, CD = 8 cm and BC = 26 cm. Find :
(i) AC
(ii) AB
(iii) area of the shaded region.
(c) In figure (iii) given below, triangle ABC is right angled at B. Given that AB = 9 cm, AC = 15 cm and D, E are mid-points of the sides AB and AC respectively, calculate
(i) the length of BC (ii) the area of ∆ADE.

Answer: (a) Given. In ∆ ABC , AD ⊥ BC, AB = 25 cm, AC = 17 cm and AD = 15 cm
Required. The length of BC.
Solution:
In right angled ∆ABD,
AB² = AD² + BD² (By Pythagoras theorem)
∴ BD² = AB² – AD²
= (25)² – (15)²
= 625 – 225 = 400
⇒ BD = \(\sqrt{400}\) = 20 cm.
Now, in right angled ∆ ADC
AC² = AD² + DC² (By Pythagoras theorem)
∴ DC²= AC² – AD²
⇒ DC² = (17)² – (15)²
⇒ DC² = 289 – 225 = 64
DC = \(\sqrt{64}\) = 8cm
Hence, BC = BD + DC = 20 cm + 8 cm = 28 cm.

(b) Given. In ∆ ABC,
∠BAC = 90°, ∠ ADC = 90° AD = 6cm, CD = 8 cm and BC = 26 cm.
Required. (i) AC (ii) AB
(iii) area of the shaded region
Solution:
In right angled ∆ ADC
AC² = AD² + DC² (By Pythagoras theorem)
= (6)² + (8)²
= 36 + 64 = 100
∴ = \(\sqrt{10}\) = 10 cm Answer:
In right angled ∆ ABC
BC² = AB² + AC² (By Pythagoras theorem)
⇒ (26)² = AB² + (10)²
⇒ AB² = (26)² – (10)²
⇒ AB² = 676 – 100 = 576
⇒ AB² = 576
⇒ AB = \(\sqrt{576}\) = 24 cm
Now, Area of A ABC = \(\frac{1}{2}\) × AB × AC
= \(\frac{1}{2}\) × 24 × 10 cm² = 12 × 10 cm² = 120 cm²
Area of ∆ ADC = \(\frac{1}{2}\) × AD × DE
= \(\frac{1}{2}\) × 6 × 8 cm² =3 × 8 cm² = 24 cm²
Now, Area of ∆ ABC = \(\frac{1}{2}\) × AB × AC
= \(\frac{1}{2}\) × 24 × 10 cm² = 12 × 10 cm² = 120 cm²
Area of ∆ ADC = \(\frac{1}{2}\) × AD × DC
= \(\frac{1}{2}\) × 6 × 8 cm² = 3 × 8 cm² = 24 cm²
Hence, area of shaded region = Area of ∆ ABC – Area of ∆ ADC = 120 cm² – 24 cm² = 96 cm²

(c) Given. In right angled ∆ ABC, AB = 9 cm, AC = 15 cm, and D, E are mid-points of the sides AB and AC respectively.
Required. (i) length of BC (ii) the area of ∆ ADE
Solution:
In right angled ∆ ADE, (By Pythagoras theorem)
AE² = AD² + DE²

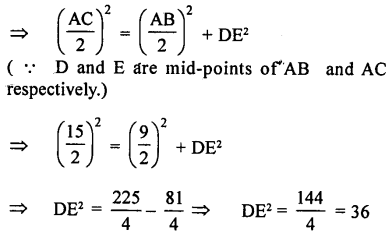
Question 2.
If in ∆ ABC, AB > AC and AD ⊥ BC, prove that AB² – AC² = BD² – CD².
Answer:
Given. In ∆ ABC, AB > AC and AD ⊥ BC
To prove. AB² – AC² = BD² – CD²

Proof. In right angled ∆ ABD
AB² = AD² + BD² …….(1) (By Pythagoras theorem
In right angled ∆ACD
AC² = AD² + CD² ……(2)
Subtracting (2) from (1), we get
AB² – AC² = (AD² + BD²) – (AD² + CD²)
= AD² + BD² – AD² – CD² = BD² – CD²
∴ AB² – AC² = BD² – CD² Hence, the result.

Question 3.
In a right angled triangle ABC, right angled at C, P and Q are the points on the sides CA and CB respectively which divide these sides in the ratio 2 : 1. Prove that
(i) 9AQ² = 9AC² + 4BC²
(ii) 9BP² = 9BC² + 4AC²
(iii) 9(AQ² + BP²) = 13AB².
Solution:
Given. A right angled ∆ ABC in which ∠C = 90°. P and Q are points on the side CA and CB respectively such that CP : AP = 2 : 1 and CQ : BQ = 2 : 1
To prove. (i) 9AQ² = 9AC² + 4BC²
(ii) 9BP² = 9BC² + 4AC²
(iii) 9 (AQ² + BP²) = 13 AB²

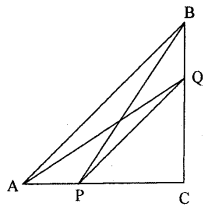
Construction. Join AQ and BP.
Proof. (i) In right angled ∆ ACQ
AQ² = AC² + QC² (By Pythagoras theorem)
9AQ² = 9AC² + 9QC² ( Multiplying both sides by 9)
= 9AC² + (3QC)² = 9AC² + (2BC)²

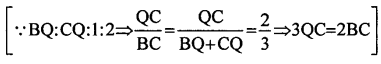
= 9AC² + 4BC²
∴ 9AQ² = 9AC² + 4BC² …..(1)

(ii) In right angled ∆ BPC
BP² = BC² + CP² (By Pythagoras theorem)
9BP² = 9BC² + 9CP² (∵ Multiplying both side by 9)
= 9BC² + (3 CP)² = 9BC² + (2AC)²

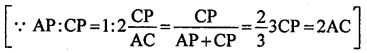
= 9BC² + 4AC²
∴ 9BP² = 9BC² + 4AC² ….(2)

(iii) Adding (1) and (2),
9AQ² + 9BP² = 9AC² + 4BC² + 9BC² + 4AC²
= 13AC² + 13BC² = 13 (AC² + BC²) = 13 AB² [In right angled ∆ ABC = AB² = AC² + BC²]
∴ 9AQ + 9BP² = 13 AB²
Hence, the result.

Question 4.
In the given figure, ∆PQR is right angled at Q and points S and T trisect side QR. Prove that 8PT² = 3PR² + 5PS².

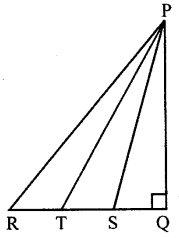
Solution:
In the ∆PQR, ∠Q = 90°
T and S are points on RQ such that these trisect it
i.e., RT = TS = SQ
To prove : 8PT² = 3PR² + 5PS²
Proof: Let RT = TS = SQ = x
In right ∆PRQ
PR² = RQ² + PQ² = (3x)² + PQ² = 9x² + PQ²
Similarly in right PTS,
PT² = TQ² + PQ² = (2x)² + PQ² = 4x² + PQ²
and in PSQ,
PS² = SQ² + PQ² = x² + PQ²
8PT² = 8(4x² + PQ²) = 32x² + 8PQ²
3PR² = 3(9x² + PQ²) = 27x² + 3PQ²
5PS² = 5(x² + PQ²) = 5x² + 5PQ²
LHS = 8PT² = 32x² + 8PQ²
RHS = 3PR² + 5PS² = 27x² + 3PQ² + 5x² + 5PQ².
= 32x² + 8PQ².
LHS = RHS
Hence proved.

Question 5.
In a quadrilateral ABCD, ∠B = 90°. If AD² = AB² + BC² + CD², prove that ∠ACD = 90°.
Solution:
In quadrilateral ABCD, ∠B = 90° and AD² = AB² + BC² + CD²
To prove : ∠ACD = 90°
Proof: In ∠ABC, ∠B = 90°
∴ AC² = AB² + BC² …(i) (Pythagoras Theorem)
But AD² = AB² + BC² + CD² (Given)

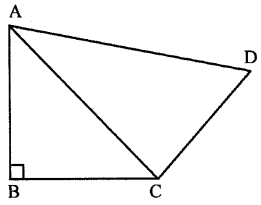
⇒ AD² = AC² + CD² [From (i)]
∴ In ∆ACD,
∠ACD = 90° (Converse of Pythagoras Theorem)

Question 6.
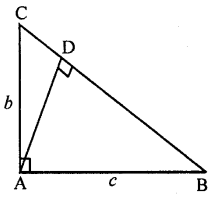
In the given figure, find the length of AD in terms of b and c.

Solution:
In the given figure,
ABC is a triangle, ∠A = 90°
AB = c, AC = b
AD ⊥ BC
To find : AD in terms of b and c
Solution:

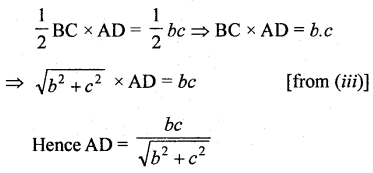
Question 7.
ABCD is a square, F is mid-point of AB and BE is one-third of BC. If area of ∆FBE is 108 cm², find the length of AC.
Solution:
Given : In square ABCD. F is mid piont of
AB and BE = \(\frac{1}{3}\) BC
Area of AFBE = 108 cm²
AC and EF are joined

To find: AC
Solution:
Let each side of square is = a
FB = \(\frac{1}{2}\) AB (F is mid point of AB)
= \(\frac{1}{2}\) a
and BE = \(\frac{1}{3}\)BC = \(\frac{1}{3}\)a
Now in square ABCD
AC = \( \sqrt2 \) × Side = \( \sqrt2 \)a
and area ∆FBE = \(\frac{1}{2}\) FB × BE
= \(\frac{1}{2}\) × \(\frac{1}{2}\)a × \(\frac{1}{2}\)a = \(\frac{1}{12}\)a²
∴ \(\frac{1}{12}\) a² = 108 ⇒ a² = 12 × 108 = 1296
⇒ a = \( \sqrt1296 \) = 36
∴ AC = \( \sqrt2 \) a = \( \sqrt2 \) × 36 = 36 \( \sqrt2 \) cm

Question 8.
In a triangle ABC, AB = AC and D is a point on side AC such that BC² = AC × CD. Prove that BD = BC.
Solution:
Given. In a triangle ABC, AB = AC and D is point on side AC such that BC² = AC × CD
To prove. BD = BC

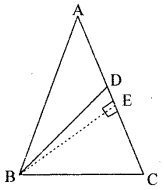
Construction. Draw BE ⊥ AC
Proof. In right angled ∆ BCE
BC² = BE² + EC² (By Pythagoras theorem)
= BE² + (AC – AE)²
= BE² + AC² + AE² -2AC.AE
= (BE² + AE²) + AC² – 2AC.AE
= AB² + AC² – 2AC.AE (In rt. ∠ ed ∆ ABC, AB² = BE² + AE²)
= AC² + AC² – 2AC.AE (given AB = AC)
= 2AC² – 2AC. AE = 2AC (AC – AE)
= 2AC.EC
But BC² = AC × CD (given)
⇒ AC × CD = 2AC.EC ⇒ CD = 2EC
∴ E is mid-points of CD ⇒ EC = DE
Now, in ∆BED and ∆ BEC
EC = DE (above proved)
BE = BE (common)
∠ BED = ∠ BEC (each 90°)
∴ ∆BED ≅ ∆ BEC (By S. A. S. axiom of congruency)
∴ BD = BC (c.p.c.t.)
Hence, the result.

ML Aggarwal Class 9 Solutions for ICSE Maths