ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 10 Triangle Chapter Test
Question 1.
In triangles ABC and DEF, ∠A = ∠D, ∠B = ∠E and AB = EF. Will the two triangles be congruent? Give reasons for your answer.
Solution:
In ∆ABC and ∆DEF
∠A = ∠D
∠B = ∠E
AB = EF
In ∆ABC, two angles and included side is given but in ∆DEF, corresponding angles are equal but side is not included of there angle.
Question 2.
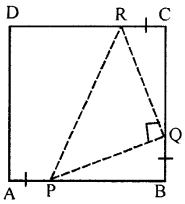
In the given figure, ABCD is a square. P, Q and R are points on the sides AB, BC and CD respectively such that AP= BQ = CR and ∠PQR = 90°. Prove that
(a) ∆PBQ = ∆QCR
(b) PQ = QR
(c) ∠PRQ = 45°
Solution:
Given: In the given figure, ABCD is a square P, Q and R are the points on the sides AB, BC and CD respectively such that AP = BQ = CR, ∠PQR = 90°
To prove : (a) ∆PBQ ≅ ∆QCR
(b) PQ = QR
(c) ∠PRQ = 45°
Proof: AB = BC = CD (Sides of square)
and AP = BQ = CR (Given)
Subtracting, we get
AB – AP = BC – BQ = CD – CR
⇒ PB = QC = RD
Now in APBQ and ∠QCR
PB = QC (Proved)
BQ = CR (Given)
∠B = ∠C (Each 90°)
∴ ∆PBQ = ∆QCR (SAS axiom)
∴ PQ = QR (c.p.c.t.)
But ∠PQR = 90° (Given)
∠RPQ = ∠PRQ (Angles opposite to equal angles)
But ∠RPQ + ∠PRQ = 90°
∠RPQ = ∠PRQ = \(\frac{90^{\circ}}{2}\) = 45°
Question 3.
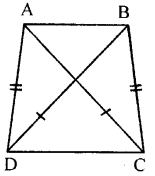
In the given figure, AD = BC and BD = AC. Prove that ∠ADB = ∠BCA.
Solution:
Given : In the figure,
AD = BC, BD = AC
To prove : ∠ADB = ∠BCA
Proof: In ∆ADB and ∆ACB
AB = AB (Common)
AD = BC (Given)
BD = AC (Given)
∆ADB = ∆ACB (SSS axiom)
∴ ∠ADB = ∠BCA (c.p.c.t.)
Question 4.
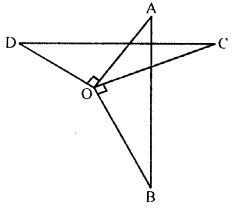
In the given figure, OA ⊥ OD, OC ⊥ OB, OD = OA and OB = OC. Prove that AB = CD.
Solution:
Given : In the figure, OA ⊥ OD, OC ⊥ OB. OD = OA, OB = OC
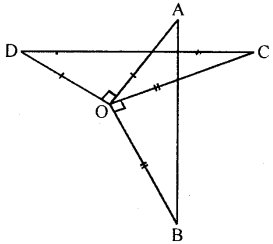
To prove : AB = CD
Proof: ∠AOD = ∠COB (each 90°)
Adding ∠AOC (both sides)
∠AOD + ∠AOC = ∠AOC + ∠COB
⇒ ∠COD = ∠AOB
Now, in ∆AOB and ∆DOC
OA = OD (given)
OB = OC (given)
∠AOB = ∠COD (proved)
∴ ∆AOB = ∆DOC (SAS axiom)
∴ AB = CD (c.p.c.t)
Question 5.
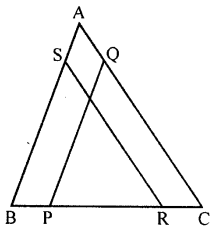
n the given figure, PQ || BA and RS CA. If BP = RC, prove that:
(i) ∆BSR = ∆PQC
(ii) BS = PQ
(iii) RS = CQ.
Solution:
Given : In the given figure,
PQ || BA, RS || CA
BP = RC
To prove :
(i) ∆BSR = ∆PQC
(ii) BS = PQ
(iii) RS = CQ
Proof: BP = RC
∵ BC – RC = BC – BP
∴ BR = PC
Now, in ∆BSR and ∆PQC
∠B = ∠P (corresponding angles)
∠R = ∠C (corresponding angles)
BR = PC (proved)
∴ ∆BSR ≅ ∆PQC (ASA axiom)
∴ BS = PQ (c.p.c.t.)
RS = CQ (c.p.c.t.)
Question 6.
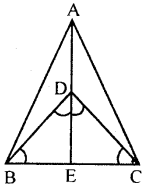
In the given figure, AB = AC, D is a point in the interior of ∆ABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ∆ABC.
Solution:
Given : In the figure given, AB = AC
D is a point in the interior of ∆ABC
Such that ∠DBC = ∠DCB
To prove : AD bisects ∠BAC
Construction : Join AD and produced it to BC in E
Proof: In ∆ABC,
AB = AC
∴ ∠B = ∠C (Angles opposite to equal sides) and ∠DBC = ∠DCB (Given)
Subtracting, we get
∠B – ∠DBC = ∠C – ∠DCB
⇒ ∠ABD = ∠ACD
Now in ∆ABD and ∆ACD
AD = AD (Common)
∠ABD = ∠ACD (Proved)
AB=AC (Given)
∴ ∆ABD ≅ ∆ACD (SAS axiom)
∴ ∠BAD = ∠CAD (c.p.c.t.)
∴ AD is bisector of ∠BAC
Question 7.
In the adjoining figure, AB || DC. CE and DE bisects ∠BCD and ∠ADC respectively. Prove that AB = AD + BC.
Solution:
Given :
In the given figure, AB || DC
CE and DE bisects ∠BCD and ∠ADC respectively

To prove : AB = AD + BC
Proof: ∵ AD || DC and ED is the transversal
∴ ∠AED = ∠EDC (Alternate angles)
= ∠ADC (∵ ED is bisector of ∠ADC)
∴ AD = AE …(i) (Sides opposite to equal angles)
Similarly,
∠BEC = ∠ECD = ∠ECB
∴ BC = EB …(ii)
Adding (i) and (ii),
AD + BC = AE + EB = AB
∴ AB = AD + BC
Question 8.
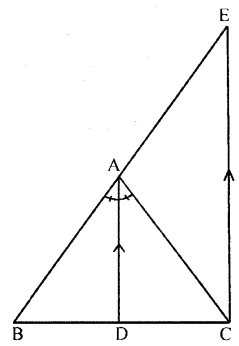
In ∆ABC, D is a point on BC such that AD is the bisector of ∠BAC. CE is drawn parallel to DA to meet BD produced at E. Prove that ∆CAE is isosceles.
Solution:
Given : In ∆ABC,
D is a point on BC such that AD is the bisector of ∆BAC
CE || DA to meet BD produced at E
To prove : ∆CAE is an isosceles
Proof: ∵ AD || EC and AC is its transversal
∴ ∠DAC = ∠ACE (Alternate angles)
and ∠BAD = ∠CEA (Corresponding angles)
But ∠BAD = ∠DAC (∵ AD is bisector of ∠BAC)
∴ ∠ACE = ∠CAE
AE = AC (Sides opposite to equal angles)
∴ ∆ACE is an isosceles triangle.
Question 9.
In the figure (it) given below, ABC is a right angled triangle at B, ADEC and BCFG are squares. Prove that AF = BE.
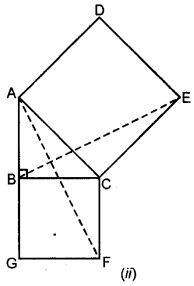
Ans.
Given. In right ∆ABC, ∠B = 90°
ADEC and BCFG are squares on the sides
AC and BC of ∆ABC respectively AF and BE are joined.
To prove. AE = BE
Proof. ∠ACE = ∠BCF
Adding ∠ACB both sides
∠ACB + ∠ACE = ∠ACB + ∠BCF
⇒ ∠∠BCE = ∠ACF
Now in ∆BCE and ∆ACF,
CF = AC (sides of a square)
BC = CF (sides of a square)
∠BCE = ∠ACF (proved)
∴ ∆BCE = ∆ACF (SAS postulate)
∴ BE = AF (c.p.c.t.)
Hence proved.
Question 10.
In the given figure, BD = AD = AC. If ∠ABD = 36°, find the value of x.
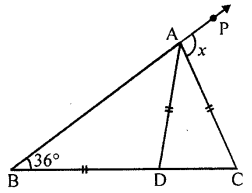
Solution:
Given : In the figure, BD = AD = AC
∠ABD = 36°
To find : Measure of x.
Proof: In ∆ABD,
AD = BD (given)
∴ ∠ABD = ∠BAD = 36° (∵ ∠ABD = 36°)
∴ Ext. ∠ADC = ∠ABD + ∠BAD (sum of interior opposite angles)
= 36° + 36° = 72°
But in ∆ADC
AD = AC
∴ ∠ADC = ∠ACD = 72°
and Ext. ∠PBC = ∠ABC + ∠ACD
= 36° + 72° = 108°
∴ x= 108°
Question 11.
In the adjoining figure, TR = TS, ∠1 = 2∠2 and ∠4 = 2∠3.
Prove that RB = SA.
Solution:
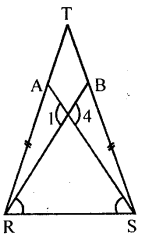
Given : In the figure, RST is a triangle
TR = TS,
∠1 = 2∠2 and ∠4 = 2∠3
To prove : RB = SA
Proof: ∠1 = ∠4 (Vertically opposite angles)
But 2∠2 = ∠1 and 2∠3 = 4
∴ 2∠2 = 2∠3
∴ ∠2 = ∠3
∴ But ∠TRS = ∠TSR (∵ TR = TS given)
∴ ∠TRS – ∠BRS = ∠TSR – ∠ASR
⇒ ∠ARB = ∠BSA
Now in ∆RBT and ∆SAT
∠T = ∠T (Common)
TR = TS (Given)
and ∠TRB = ∠TSA (proved)
∴ ∆RBT ≅ ∆SAT
∴ RB = SA
Question 12.
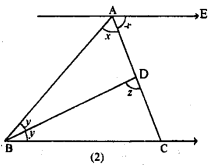
(a) In the figure (1) given below, find the value of x.
(b)In the figure (2) given below, AB = AC and DE || BC. Calculate
(i) x
(ii) y
(iii) ∠BAC
(c) In the figure (1) given below, calculate the size of each lettered angle.
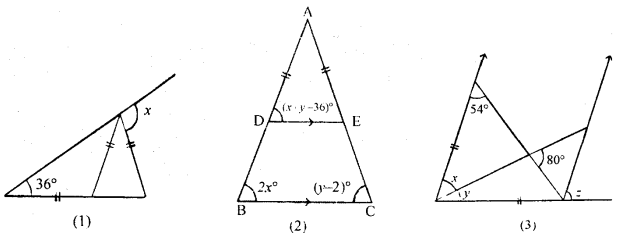
Solution:
(a) We have to calculate the value of x.
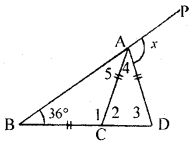
Now, in ∆ ABC
∠5 = 36° (1)
Also, 36° + ∠ 1 + ∠ 5 = 180° [ ∵AC = BC] [sum of all angles in a triangle is 180°]
⇒ 36°+ ∠1 + 36° = 180° [from (1)]
⇒ 72° + ∠ 1 = 180° ⇒ ∠ 1 = 180° – 72°
⇒ ∠ 1 = 108° ….. (2)
Also, ∠1 + ∠2 = 180° (Linear pair)
⇒ 108° + ∠2 = 180° [From (2)]
⇒ ∠2 = 180° – 108° ⇒ ∠2 = 72° …..(3)
Also, ∠2 = ∠3 (AC = AD)
⇒ ∠ 3 = 72° [From (3)] (4)
Now, in ∆ ACD
∠2 + ∠3 + ∠4 = 180° [sum of all angles in a triangle is 180°]
⇒ 72° + 72° + ∠4 = 180° [From (3) and (4)]
⇒ 144° + ∠4 = 180° ⇒ ∠4 = 180° – 144°
⇒ ∠4 = 36° (5)
∴ ABP is a St. line
∴ ∠5 + ∠4 + x=180°
36° + 36°’+ x = 180° [From (1) and (5)]
72° + x = 180 ⇒ x = 108°
Hence, value of x = 108°
(b) Given. AB = AC, and DE || BC
∠ADE = (x + y -36)°
∠ ABC = 2x°and ∠ ACB = (y – 2)°
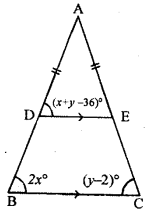
To Calculate. (i) x (ii) y (iii) ∠ BAC
Now, in ∆ABC
∴ AB = AC
2x = y – 2
[In a triangle equal sides here equal angle opposite to them]
2x – y = -2 …..(1)
∴ DE || BC,
x + y – 36 = 2x [corresponding angles]
⇒ x + y – 2x = 36 ⇒ -x + y = 36 …..(2)
From equation (1) and (2),
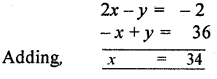
Substituting the value of x in equation (1), we get
2 × 34 -y = – 2 ⇒ 68 – y = – 2
⇒ 68 + 2 = y ⇒ 70 = y ⇒ y = 70
Hence, value of x = 34° and value of y = 70°
(iii) In ∆ ABC
∠BAC + 2 x° + (y – 2)° = 180° [sum of all angles in a triangle is 180°]
⇒ ∠ BAC + 2 × 34°+ (70 – 2)°= 180° (Substituting the value of x and y)
⇒ ∠BAC + 68°+ 68° = 180°
⇒ ∠BAC = 180°- 136° ⇒ ∠BAC = 44°
Hence, value of ∠ BAC = 44°
(c) Given. ∠BAE = 54°, ∠DEC = 80° and AB = BC.
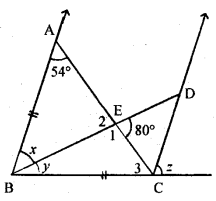
To calculate. The value of x, y and z.
Now ∠ 2 = 80° …………(1) (vertically opposite angles
∴ AC and BD cut at point E)
In ∆ ABE,
54° +x + ∠2 = 180° (sum of all angles in triangle is 180°)
⇒ 54°+ x + 80° = 180° (∵ ∠2 = 80°)
⇒ 134° + x = 180° ⇒ x = 180° – 134°
⇒ x = 46°
Now, ∠1 + 80° = 180° (Linear pair)
∠1 = 180°-80° ⇒ ∠l = 100° …….(2)
Also, AB = BC (given)
∠3 = 54°
(In a triangle equal sides have equal angles)
Now, in ∆ ABC
54° + (x + y) + ∠3 = 180° (substituting the value of x and ∠ 3)
⇒ 154° + y = 180° ⇒ y = 180° – 154°
⇒ y = 26° ….(3)
∴ AB || CD, ∴ x + y = z [corresponding angles]
⇒ 46° + 26° = z [From (2) and (3)]
⇒ z = 46° + 26° ⇒ z = 72°
Hence, value of x = 46°, y = 26° and z = 72° Ans.
Question 13.
(a) In the figure (1) given below, AD = BD = DC and ∠ACD = 35°. Show that
(i) AC > DC
(ii) AB > AD.
(b) In the figure (2) given below, prove that
(i) x + y = 90°
(ii) z = 90°
(iii) AB = BC
Solution:
(a) Given: In the figure given,
AD = BD = DC
∠ACD = 35°
To prove : (i) AC > DC, (ii) AB > AD
Proof: In ∆ ADC, AD = DC
∴ ∠DAC = ∠DCA = 35°
⇒ ∠ADC = 180° – (∠DAC + ∠DCA)
∴ ∠ADC = 180° – (35° + 35°)
= 180° – 70°= 110°
and Ext. ∠ADB = ∠DAC + ∠DCA = 35° + 35° = 70°
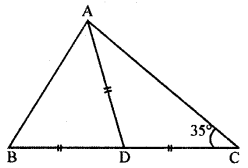
∵ AD = BD
∠BAD = ∠ABD
But ∠BAD + ∠ABD = 180° – ∠ADB
⇒ ∠ABD + ∠ABD = 180° – 70° = 110°
⇒ 2∠ABD = 110° ⇒ ∠ABD = \(\frac{110^{\circ}}{2}\) = 55°
(i) Now v ∠ADC > ∠DAC
∴ AC > DC
and ∠ADB > ∠ABD
∴ AB > AD
(b) Given. ∠ EAC = ∠ BAC = x
∠ ABD = ∠ DBC = y
∠BDC = z
To prove. (i) x + y = 90°
(ii) z = 90°
(iii) AB = BC
Proof. (i) ∴ AE || BC
∴ ∠ ACB = x [Alternate angles] …….(1)
In ∆ ABC
x + (y + y) + ∠ ACB = 180° [sum of all angles in a triangle is 180°]
⇒ x + 2y + x = 180° [From (1)]
⇒ 2x + 2y =180°
⇒ 2 (x + y) = 180° (proved) ……..(2)
⇒ x + y = 90°
(ii) Now, in ∆ BCD,
y + z + ∠BCD = 180° [sum of all angles in a triangle is 180°]
⇒ y + z + x = 180°
⇒ 90° + z = 180° [From (2) , x + y = 90°]
⇒ z = 90° (proved) …..(3)
(iii) In ∆ ABC
∠ BAC ∠ B AC = x (each same value)
∴ AB = CB (In a triangle equal angles has equal sides) (proved)
Question 14.
In the given figure, ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Solution:
Given : In the figure, two isosceles triangles ABC and DBC are on the same base BC. With vertices A and D on the same side of BC.
AD is joined and produced to meet BC at P.
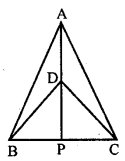
To prove:
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
Proof: ∵ ∆ABC and ∆DBC are isosceles
AB = AC and DB = DC
(i) Now in ∆ABD and ∆ACP
AB = AC (Proved)
DB = DC (Proved)
AD = AD (Common)
∴ ∆ABD ≅ ∆ACD (SSS axiom)
∴ ∠BAD = ∠CAD (c.p.c.t.)
∴ADP bisects ∠A
and ∠ADB = ∠ADC (c.p.c.t.)
But ∠ADB + ∠BDP = ∠CAD + ∠CDP = 180°
∴ ∠BDP = ∠CDP
∴ ADP bisects ∠D also
Now in ∆APB and ∆ACD
AB = AC (Given)
AP = AP (Common)
and ∠BAD = ∠CAD (Proved)
∴ ∠APB ≅ ∆ACP (ASA axiom)
∴ BP = CP (c.p.c.t)
and ∠APB = ∠APC
But ∠APB + ∠APC = 180°
∴ ∠APB = ∠APC = 90°
and BP = PC
∴ AP is perpendicular bisector of BC
Question 15.
In the given figure, AP ⊥ l and PR > PQ. Show that AR > AQ.
Solution:
Given : In the given figure,
AP ⊥ l and PR > PQ
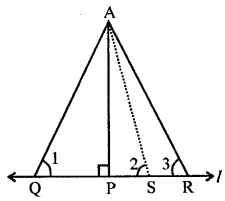
To prove : AR > AQ
Construction : Take a point S on l,
Such that PS = PQ
Join A and S
Proof: In ∆AQP and ∆ASP
AP = AP (Common)
QP = SP (Given)
∠APQ = ∠APS (Each 90°)
∴ ∆APQ ≅ ∆APS
∴∠1 = ∠2
AQ = AS (Sides opposite to equal angles)
In ∆ASR
Ext. ASP > ∠ARS
⇒ ∠2 > ∠3
⇒ ∠1 > ∠3 (∵ ∠1 = ∠2)
⇒ AR > AQ
Question 16.
If O is any point in the interior of a triangle ABC, show that
OA + OB + OC > \(\frac{1}{2}\)
(AB + BC + CA).
Solution:
Given : In the figure, O is any point in the interior of ∆ABC.
To prove : OA + OB + OC > \(\frac{1}{2}\) (AB + BC + CA)
Construct: Join B and C.
Proof: In AOBC
OB + OC > BC …(i)
(Sum of two sides of a triangle is greater than its third side)
Similarly OC + OA > CA
and OA + OB > AB
Adding are get,
(OB + OC + OC + OA + OA + OB) > BC + CA + AB
⇒ 2(OA + OB + OC) > AB + BC +CA
⇒ OA + OB + OC > \(\frac{1}{2}\) (AB + BC + CA)
Question P.Q.
Construct a triangle ABC given that base BC = 5.5 cm, ∠ B = 75° and height = 4.2 cm. Ans. Given. In a triangle ABC, Base BC = 5.5. cm, ∠B = 750° and height = 4.2 cm.
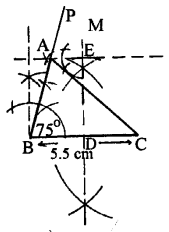
Solution:
To construct a triangle ABC.
Steps of Construction :
(1) Draw a line BC = 5.5 cm.
(2) Draw ∠PBC = 75°.
(3) Draw the perpendicular bisector of BC and cut the BC at point D.
(4) Cut the DM at point E such that DE = 4.2 cm.
(5) Draw the line at point which is parallel to line BC.
(6) This parallel line cut the BP at point A.
(7) Join AC.
(8) ABC is the required triangle.
Question P.Q.
Construct a triangle ABC in which BC = 6.5 cm, ∠ B = 75° and ∠ A = 45°. Also construct median of ∆ ABC passing through B. Given. In ∆ ABC , BC = 6.5 cm, ∠B = 75° and ∠ A = 45°.
Solution:
(i) To construct a triangle ABC.
(ii) Construct median of ∆ ABC passing through B.

Step of Construction.
(1) Draw a line BC = 6.5 cm.
(2) Make ∠PBC = 75°.
(3) Make ∠BCQ = 60°.
(4) BP and CQ cut at point A.
(5) ABC is the required triangle.
(6) Draw the bisector of AC.
(7) The bisector line cut the line AC at point D.
(8) Join BD.
(9) BD is the required median of A ABC passing through B.
Question P.Q.
Construct triangle ABC given that AB – AC = 2.4 cm, BC = 6.5 cm. and ∠ B = 45°. Ans. Given. A triangle ABC in which AB – AC = 2.4 cm, BC = 6.5 cm, ∠B = 4.5°.
Solution:
To construct a triangle ABC.

Steps of Construction :
(1) Draw BC = 6.5 cm.
(2) Draw BP making angle 65° with BC.
(3) From BP, cut BD = 2.4 cm.
(4) Join D and C.
(5) Draw perpendicular bisector of DC which cuts BP at A.
(6) Join A and C.
(7) ABC is the required triangle.