Factorization Class 10 ICSE ML Aggarwal Chapter Test

ML Aggarwal Class 10 Solutions Factorization Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Factorization Chapter Test.

ML Aggarwal SolutionsICSE SolutionsSelina ICSE Solutions

Question 1.
Find the remainder when 2x³ – 3x² + 4x + 7 is divided by
(i) x – 2
(ii) x + 3
(iii) 2x + 1
Solution:
f(x) = 2x³ – 3x² + 4x + 7
(i) Let x – 2 = 0, then x = 2
Substituting value of x in f(x)
f(2) = 2 (2)³ – 3 (2)² + 4 (2) + 7
= 2 × 8 – 3 × 4 + 4 × 2 + 7
= 16 – 12 + 8 + 7 = 19
Remainder = 19 Ans.
(ii) Let x + 3 = 0, then x = – 3
Substituting the value of x in f(x)

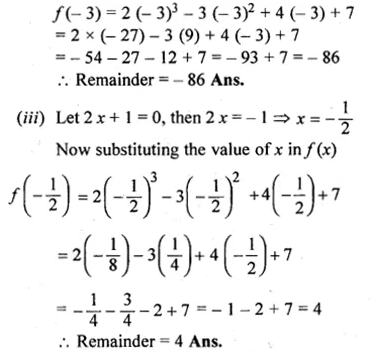
Question 2.
When 2x³ – 9x² + 10x – p is divided by (x + 1), the remainder is – 24.Find the value of p.
Solution:
Let x + 1 = 0 then x = – 1,
Substituting the value of x in f(x)
f(x) = 2x³ – 9x² + 10x – p

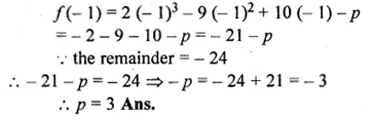
Question 3.
If (2x – 3) is a factor of 6x² + x + a, find the value of a. With this value of a, factorise the given expression.
Solution:
Let 2 x – 3 = 0 then 2x = 3
=>x = \(\\ \frac { 3 }{ 2 } \)
Substituting the value of x in f(x)

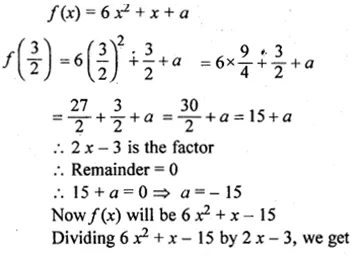
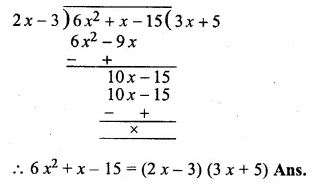
Question 4.
When 3x² – 5x + p is divided by (x – 2), the remainder is 3. Find the value of p. Also factorise the polynomial 3x² – 5x + p – 3.
Solution:
f(x) = 3x² – 5x+ p
Let (x – 2) = 0, then x = 2
f(2) = 3 (2)² – 5(2) + p
= 3 x 4 – 10 + p
= 12 – 10 + p
= 2 + p

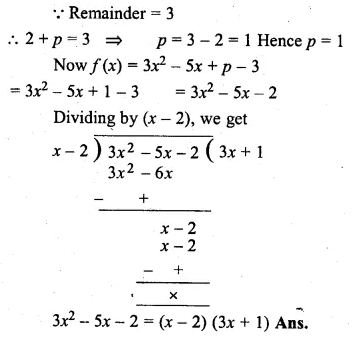
Question 5.
Prove that (5x + 4) is a factor of 5x³ + 4x² – 5x – 4. Hence factorise the given polynomial completely.
Solution:
f(x) = 5x³ + 4x² – 5x – 4
Let 5x + 4 = 0, then 5x = – 4
=> x = \(\\ \frac { -4 }{ 2 } \)

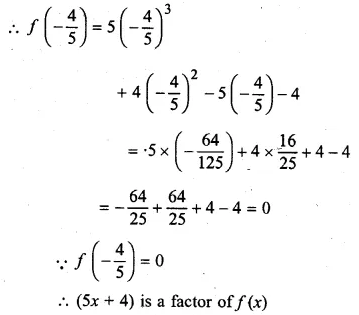
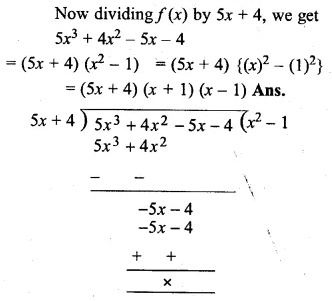
Question 6.
Use factor theorem to factorise the following polynomials completely:
(i) 4x³ + 4x² – 9x – 9
(ii) x³ – 19x – 30
Solution:
(i) f(x) = 4x³ + 4x² – 9x – 9
Let x = – 1,then
f( – 1) = 4 ( – 1)³ + 4 ( – 1)² – 9 ( – 1) – 9

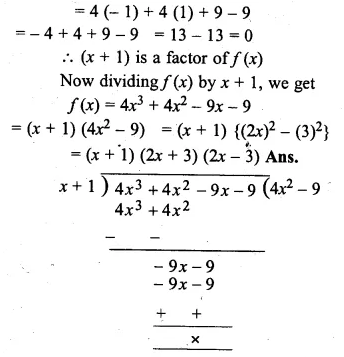
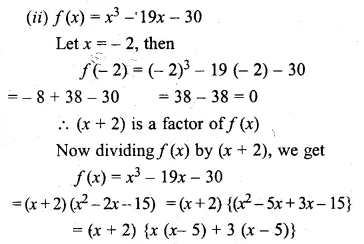
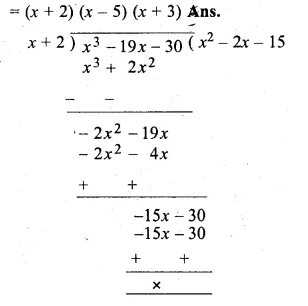
Question 7.
If x³ – 2x² + px + q has a factor (x + 2) and leaves a remainder 9, when divided by (x + 1), find the values of p and q. With these values of p and q, factorise the given polynomial completely.
Solution:
f(x) = x³ – 2x² + px + q
(x + 2) is a factor
f( – 2) = ( – 2)³ – 2( – 2)² + p ( – 2) + q

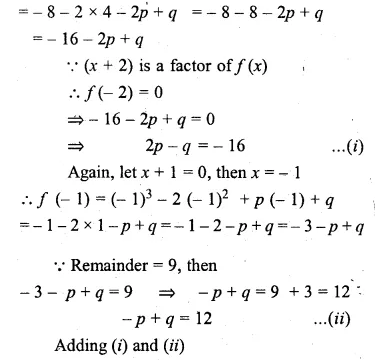
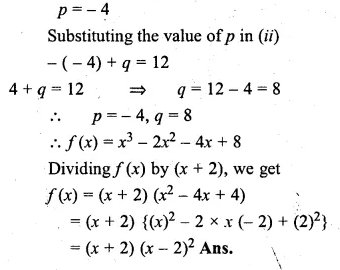
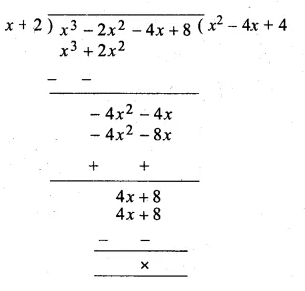
Question 8.
If (x + 3) and (x – 4) are factors of x³ + ax² – bx + 24, find the values of a and b: With these values of a and b, factorise the given expression.
Solution:
f(x) = x³ + ax² – bx + 24
Let x + 3 = 0, then x = – 3
Substituting the value of x in f(x)

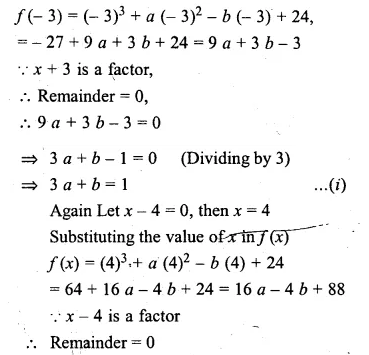
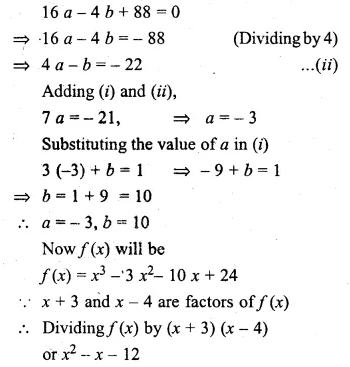
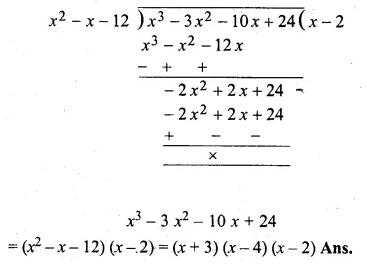
Question 9.
If 2x³ + ax² – 11x + b leaves remainder 0 and 42 when divided by (x – 2) and (x – 3) respectively, find the values of a and b. With these values of a and b, factorise the given expression.
Solution:
f(x) = 2x³ + ax² – 11 x + b
Let x – 2 = 0, then x = 2,
Substituting the vaue of x in f(x)

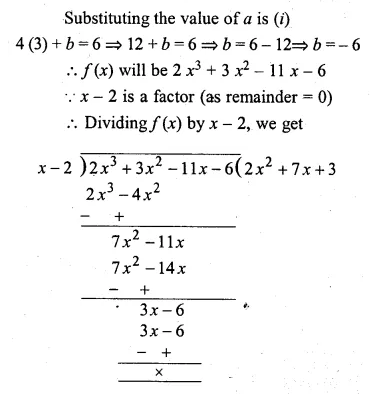
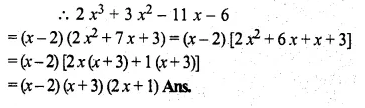
Question 10.
If (2x + 1) is a factor of both the expressions 2x² – 5x + p and 2x² + 5x + q, find the value of p and q. Hence find the other factors of both the polynomials.
Solution:
Let 2x + 1 = 0, then 2x = – 1
x = \(– \frac { 1 }{ 2 } \)
Substituting the value of x in

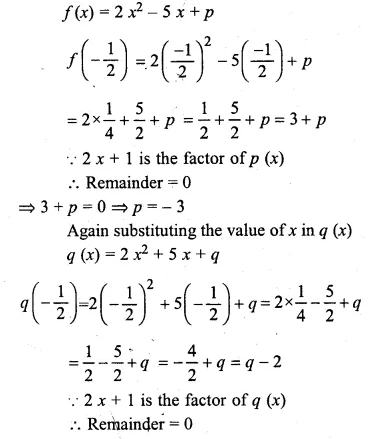
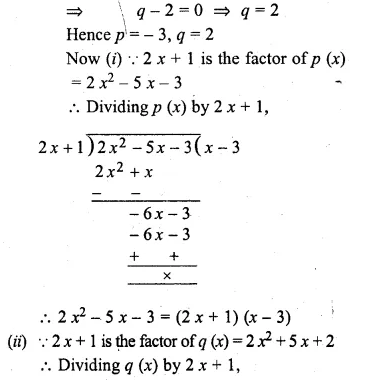
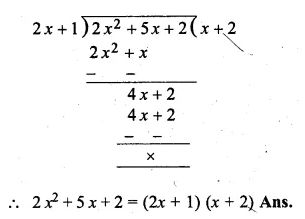
Question 11.
When a polynomial f(x) is divided by (x – 1), the remainder is 5 and when it is,, divided by (x – 2), the remainder is 7. Find – the remainder when it is divided by (x – 1) (x – 2).
Solution:
When f(x) is divided by (x – 1),
Remainder = 5
Let r – 1 = 0 => x = 1

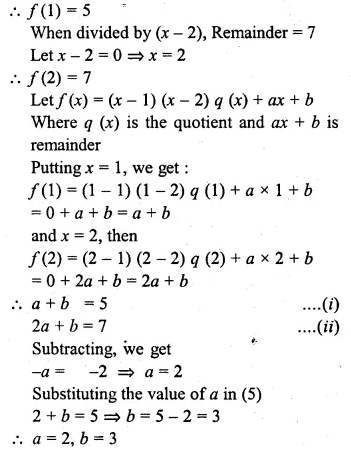
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Factorization Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. APlusTopper try to provide online math tutoring for you.