ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Linear Inequations Chapter Test

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Linear Inequations Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Linear Inequations Chapter Test.

ML Aggarwal SolutionsICSE SolutionsSelina ICSE Solutions

Question 1.
Solve the inequation : 5x – 2 ≤ 3(3 – x) where x ∈ { – 2, – 1, 0, 1, 2, 3, 4}. Also represent its solution on the number line.
Solution:
5x – 2 < 3(3 – x)
=> 5x – 2 ≤ 9 – 3x
=> 5x + 3x ≤ 9 + 2

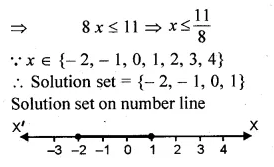
Question 2.
Solve the inequations :
6x – 5 < 3x + 4, x ∈ I.
Solution:
6x – 5 < 3x + 4
6x – 3x < 4 + 5
=> 3x <9
=> x < 3
x∈I
Solution Set = { – 1, – 2, 2, 1, 0….. }

Question 3.
Find the solution set of the inequation
x + 5 < 2 x + 3 ; x ∈ R
Graph the solution set on the number line.
Solution:
x + 5 ≤ 2x + 3
x – 2 x ≤ 3 – 5
=> – x ≤ – 2
=> x ≥ 2

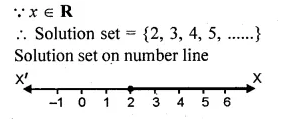
Question 4.
If x ∈ R (real numbers) and – 1 < 3 – 2x ≤ 7, find solution set and represent it on a number line.
Solution:
– 1 < 3 – 2x ≤ 7
– 1 < 3 – 2x and 3 – 2x ≤ 7
2 x < 3 + 1 and – 2x ≤ 7 – 3
2 x < 4 and – 2 x ≤ 4
x < 2 and – x ≤ 2
and x ≥ – 2 or – 2 ≤ x
x∈R
Solution set – 2 ≤ x < 2
Solution set on number line

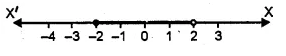
Question 5.
Solve the inequation :
\(\frac { 5x+1 }{ 7 } -4\left( \frac { x }{ 7 } +\frac { 2 }{ 5 } \right) \le 1\frac { 3 }{ 5 } +\frac { 3x-1 }{ 7 } ,x\in R\)
Solution:
\(\frac { 5x+1 }{ 7 } -4\left( \frac { x }{ 7 } +\frac { 2 }{ 5 } \right) \le 1\frac { 3 }{ 5 } +\frac { 3x-1 }{ 7 } \)
\(\frac { 5x+1 }{ 7 } -4\left( \frac { x }{ 7 } +\frac { 2 }{ 5 } \right) \le \frac { 8 }{ 5 } +\frac { 3x-1 }{ 7 } \)

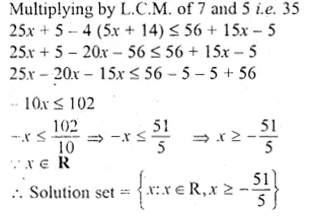
Question 6.
Find the range of values of a, which satisfy 7 ≤ – 4x + 2 < 12, x ∈ R. Graph these values of a on the real number line.
Solution:
7 < – 4x + 2 < 12
7 < – 4x + 2 and – 4x + 2 < 12

Question 7.
If x∈R, solve \(2x-3\ge x+\frac { 1-x }{ 3 } >\frac { 2 }{ 5 } x\)
Solution:
\(2x-3\ge x+\frac { 1-x }{ 3 } >\frac { 2 }{ 5 } x\)
\(2x-3\ge x+\frac { 1-x }{ 3 } \) and \(x+\frac { 1-x }{ 3 } >\frac { 2 }{ 5 } x\)

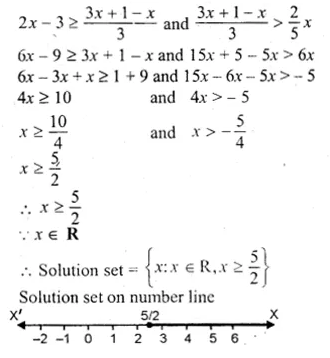
Question 8.
Find positive integers which are such that if 6 is subtracted from five times the integer then the resulting number cannot be greater than four times the integer.
Solution:
Let the positive integer = x
According to the problem,
5a – 6 < 4x
5a – 4x < 6 => x < 6
Solution set = {x : x < 6}
= { 1, 2, 3, 4, 5, 6} Ans.

Question 9.
Find three smallest consecutive natural numbers such that the difference between one-third of the largest and one-fifth of the smallest is atleast 3.
Solution:
Let first least natural number = x
then second number = x + 1
and third number = x + 2

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Linear Inequations Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. APlusTopper try to provide online math tutoring for you.