Math Labs with Activity – Verify the Identity a³ + b³ =(a+b)(a² -ab+b²)

Math Labs with Activity – Verify the Identity a³ + b³ =(a+b)(a² -ab+b²)

OBJECTIVE

To verify the identity a³ + b³ =(a+b)(a² -ab+b²) using a set of unit cubes

Materials Required
A set of 56 plastic cubes where each cube has dimensions (1 unit x 1 unit x 1 unit).

Procedure
We shall verify the identity for a = 3 and b = 1.
Step 1: We shall make Arrangement 1 for 28 cubes.
This arrangement will consist of two stacks as shown in Figures 4.1(a) and 4.1(b). The total volume of this arrangement of cubes is calculated (see the calculations).

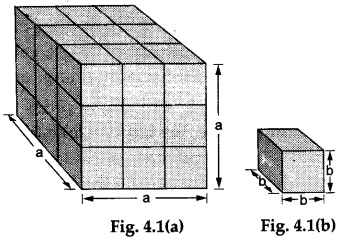
Step 2: We shall now make Arrangement 2 for the remaining 28 cubes.
This arrangement will consist of two stacks as shown in the Figures 4.2(a) and 4.2(b). The total volume of this arrangement of cubes is calculated (see the calculations).

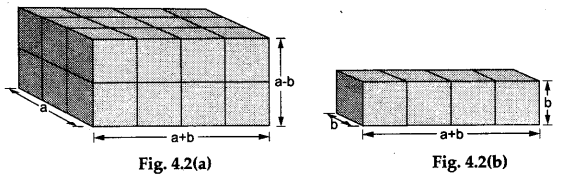
Observations
Since the two arrangements have equal number of cubes (each arrangement has 28 cubes) and all the cubes have the same volume (1 cubic unit), the total volume in both the cases must be the same.

Calculations

1. Volume of Arrangement 1
   Volume of the stack in Figure 4.1(a) = a³.
   Volume of the stack in Figure 4.1(b) = b³.
   total volume of the arrangement=(a³ + b³).
2. Volume of Arrangement 2
   Volume of the stack in Figure 4.2(a) =(a+b)(a -b)a.
   Volume of the stack in Figure 4.2(b) = (a+b)b².
   total volume of the arrangement = (a+b)(a -b)a + (a+b)b²
   =(a+b){(a-b)a+b²} =(a+b)(a² -ab +b²).
   Since the total volume in the two arrangements is the same, therefore a³ + b³ =(a+b)(a² -ab+b²).

Result
It is verified that a³ + b³ =(a+b)(a² -ab+b²).

Remarks: The students must try to verify this identity for other values of a and b by taking required number of cubes and arranging them suitably.

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills