A Plus Topper

Improve your Grades

Math Labs with Activity - Find the Orthocentre of a Given Triangle

by

Math Labs with Activity – Find the Orthocentre of a Given Triangle

OBJECTIVE

To find the orthocentre of a given triangle by the method of paper folding.

Materials Required

  1. Three sheets of white paper
  2. A geometry box

Theory
The altitude of a triangle corresponding to any side is the length of the perpendicular drawn from the opposite vertex to that side. The altitudes of a triangle are concurrent. The point of intersection of all the three altitudes of a triangle is called its orthocentre.

Procedure
Step 1: We shall first find the orthocentre of an acute-angled triangle. Draw an acute-angled triangle ABC on a sheet of white paper.
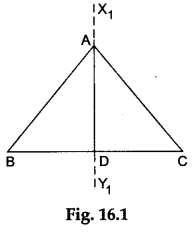
Step 2: Fold the paper along the line that passes through the point A and cuts the line BC such that the part of the line BC that lies on one side of the line of fold falls over the other part. Make a crease and unfold the paper. Draw a line X1Y1 along the crease. Label the point D where the line intersects the line BC. Then, AD is an altitude of ΔABC corresponding to the side BC as shown in Figure 16.1.
Math Labs with Activity - Find the Orthocentre of a Given Triangle 1
Step 3: Fold the paper along the line that passes through the point B and cuts the line AC such that the part of the line AC that lies on one side of the line of fold falls over the other part. Make a crease and unfold the paper. Draw a line X2Y2 along the crease. Label the point E where the line X2Y2 intersects the line AC. Then, BE is an altitude of ΔABC corresponding to the side AC as shown in Figure 16.2.
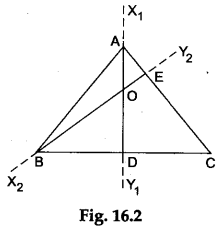
Math Labs with Activity - Find the Orthocentre of a Given Triangle 2
Step 4: Label the point O where the altitudes AD and BE intersect. Then, point O is the orthocentre of the acute-angled triangle ABC. What do you observe?
Step 5: We shall now find the orthocentre of a right-angled triangle. Draw a right-angled triangle HIJ (right-angled at vertex f) on another sheet of white paper.
Step 6: Fold the paper along the line that passes through the point I and cuts the line HJ such that the part of the line HJ that lies on one side of the line of fold falls over the other part. Make a crease and
unfold the paper. Draw a line X3Y3 along the crease. Label the point K where the line X3Y3 intersects the line HJ. Then, IK is an altitude of ΔHIJ corresponding to the side HJ as shown in Figure 16.3.
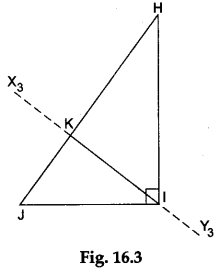
Math Labs with Activity - Find the Orthocentre of a Given Triangle 3
Step 7: The side HI is the altitude of ΔHIJ corresponding to the side IJ and the side IJ is the altitude of ΔHIJ corresponding to the side HI. The point of intersection of the three altitudes IK, HI and IJ is the point I. Therefore, the point I is the orthocentre of the right-angled triangle HIJ. Record your observations.
Step 8: We shall now find the orthocentre of an obtuse-angled triangle. Draw an obtuse-angled triangle PQR (∠PQR being obtuse) on the third sheet of white paper.
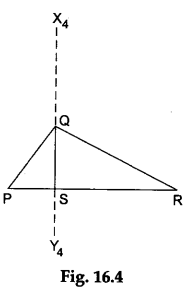
Step 9: Fold the paper along the line that passes through the point Q and cuts the line PR such that the part of the line PR that lies on one side of the line of fold falls on the other part. Make a crease and unfold the paper. Draw a line X4Y4 along the crease. Label the point S where the line X4Y4 intersects the line PR. Then, the line QS is an altitude of ΔPQR corresponding to the side PR as shown in Figure 16.4.
Math Labs with Activity - Find the Orthocentre of a Given Triangle 4
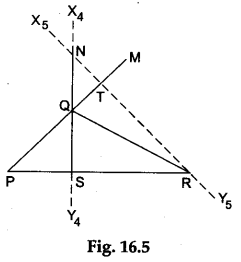
Step 10: Produce the line PQ to a point M as shown in Figure 16.5. Fold the paper along the line that passes through the point R and cuts the line PM such that the part of the line PM that lies on one side of the line of fold falls on the other part. Make a crease and unfold the paper. Draw a line X5Y5 along the crease. Label the point T where the line X5Y5 intersects the line PM. Then, the line RT is an altitude of ΔPQR corresponding to the side PQ (produced) as shown in Figure 16.5.
Step 11: Label the point N where the two altitudes RT (produced) and SQ (produced) intersect (i.e., where the lines X4Y4 and X5Y5 intersect). Then, the point N is the orthocentre of the obtuse¬angled triangle PQR. Record your observations.
Math Labs with Activity - Find the Orthocentre of a Given Triangle 5

Observations and Results

  1. The orthocentre of an acute-angled triangle lies inside the triangle.
  2. The orthocentre of a right-angled triangle lies on the vertex of the right angle.
  3. The orthocentre of an obtuse-angled triangle lies outside the triangle.

Remarks: Since all the altitudes meet at a single point, it is sufficient to find the point of intersection of only two altitudes to obtain the orthocentre of a triangle.

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills