Math Labs with Activity - Equal Chords of a Circle Subtend

Math Labs with Activity – Equal Chords of a Circle Subtend

OBJECTIVE

To verify that equal chords of a circle subtend equal angles at the centre of the circle

Materials Required

1. A sheet of white paper
2. A piece of cardboard
3. A sheet of tracing paper
4. A geometry box
5. A tube of glue

Theory
A line segment joining any two points on a circle is called a chord of the circle. Any two equal chords of a circle subtend equal angles at the centre of the circle.
The theorem can be proved as below.
Consider a circle with radius r and centre O and having two equal chords AB and PQ as shown in Figure 15.1.

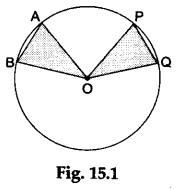
In ΔAOB and POQ, we have

1. AO=OP (each equal to r)
2. BO =OQ (each equal to r)
3. AB = PQ (equal chords)

Then, ΔAOB is congruent to ΔPOQ (by SSS-criterion).
∴ ∠AOB = ∠POQ.

Procedure
Step 1: Paste the white paper on the cardboard and draw a circle with centre O on this paper.
Step 2: Take a pair of compasses. Placing its needle point at a point A on the circle and taking any radius, draw an arc cutting the circle at some point B. Joining AB we get a chord of the circle.
Taking the same radius and again placing the needle point of the compasses at another point P on the circle, draw an arc cutting the circle at some point Q. Joining PQ we get another chord which is equal to the chord AB.
Step 3: Join AO and BO to form the triangle AOB. Also, join PO and QO to form the triangle POQ (see Figure 15.2).

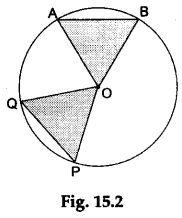
Step 4: Trace the ΔAOB on the tracing paper.
Step 5: Place the ΔAOB obtained on the tracing paper over the ΔPOQ such that AB overlaps PQ.

Observations
We observe that the ΔAOB completely overlaps the ΔPOQ. Therefore, the ΔAOB is congruent to the ΔPOQ.
So, we conclude that ∠AOB = ∠POQ.

Result
It is verified that equal chords of a circle subtend equal angles at the centre of the circle.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs