Math Labs with Activity – Equal Chords of a Circle are Equidistant
OBJECTIVE
To verify that equal chords of a circle are equidistant from the centre of the circle
Materials Required
- A sheet of transparent paper
- A geometry box
Theory
The length of the perpendicular drawn from the centre of a circle to a chord gives the distance of the chord from the centre of the circle.
Procedure
Step 1: Mark a point O on the sheet of transparent paper.
With O as the centre, draw a circle of any radius.
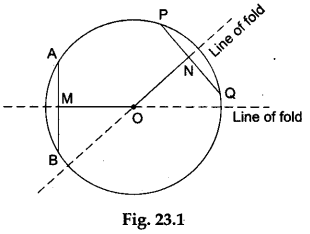
Step 2: Draw two equal chords AB and PQ in this circle. (Adopt the procedure discussed in Activity 15.)
Step 3: Fold the paper along the line which passes through O and cuts the chord AB such that one part of the chord AB overlaps the other part.
Make a crease and unfold the paper. Mark the point M where the line of fold cuts the chord AB. Join OM. Then, OM ⊥ AB. Thus, OM is the distance of the chord AB from the centre O of the circle.
Step 4: Again fold the paper along the line which passes through O and cuts the chord PQ such that one part of the chord PQ overlaps the other part.
Make a crease and unfold the paper. Mark the point N where the line of fold cuts the chord PQ. Join ON. Then, ON ⊥ PQ. Thus, ON is the distance of chord PQ from the centre O of the circle.
Step 5: Fold the paper along the line passing through the centre O of the circle such that the line OM overlaps the line ON.
Observations
When the paper is folded along the line passing through O such that the line OM overlaps the line ON, we observe that the point M lies exactly over the point N.
Therefore, OM =ON, i.e., the distance of the chord AB from O = the distance of the chord PQ from O.
Result
It is verified that equal chords of a circle are equidistant from the centre of the circle.
Math Labs with ActivityMath LabsScience Practical SkillsScience Labs