Math Labs with Activity - Determine the Total Surface Area

Math Labs with Activity – Determine the Total Surface Area

OBJECTIVE

To determine the total surface area of

1. a right-triangular prism
2. a right-triangular pyramid (a regular tetrahedron)

Materials Required

1. Cardboard models of a right-triangular prism and a right-triangular pyramid
2. A cutter

Theory
There are two types of right-triangular prisms:
Type I – It has two congruent equilateral triangles as bases and three congruent squares forming the lateral surfaces. Such a prism is shown in Figure 34.1(a).

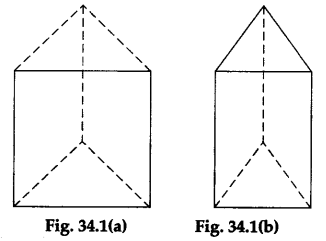
Type II – It has two congruent equilateral triangles as bases and three congruent rectangles forming the lateral surfaces. Such a prism is shown in Figure 34.1(b).
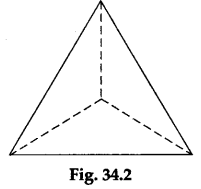
The right-triangular pyramid (also called the regular tetrahedron) has four congruent equilateral triangles, out of which any one forms the base and the remaining ones form the lateral surfaces. A regular tetrahedron is shown in Figure 34.2.

Procedure
Step 1: Cut (using the cutter) the model of the right-triangular prism shown in Figure 34.1(a) along its edges and open it up to obtain a figure of the form as shown in Figure 34.3(a).

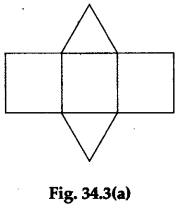
Step 2: The two faces forming the bases are congruent equilateral triangles and the three faces forming the lateral surfaces are congruent squares. The total surface area of the prism is therefore the total area of all the five faces (see Calculations, Case I).
Step 3: Cut the model of the right-triangular prism shown in Figure 34.1(b) along its edges and open it up to obtain a figure of the form shown in Figure 34.3(b).

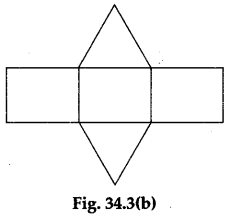
Step 4: The two faces forming the bases are congruent equilateral triangles and the three faces forming the lateral surfaces are congruent rectangles. The total surface area of the prism is therefore the total area of all the five faces (see Calculations, Case II).
Step 5: Cut the model of the regular tetrahedron (right-triangular pyramid) shown in Figure 34.2 along its edges and open it up to obtain a figure of the form shown in Figure 34.4.

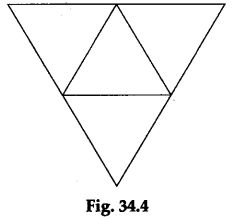
Step 6: All the four faces are congruent equilateral triangles and the sum of the areas of these triangles will give the total area of the tetrahedron (see Calculations, Case III).

Calculations
Case I – The total lateral surface area of the prism [Figure 34.1(a)] = 3 x area of each square face.
The total area of the bases = 2 x the area of each equilateral triangular face.
∴ the total surface area = total lateral surface area + total area of the bases.
Case II – The total lateral surface area of the prism [Figure 34.1(b)] = 3 x the area of each rectangular face.
The total area of the bases = 2 x the area of each equilateral triangular surface.
∴ the total surface area = total lateral surface area + total area of the bases.
Case III – The total surface area of the regular tetrahedron (Figure 34.2)
= 4 x the area of each equilateral triangular face.

Result
The total surface area of a prism or a pyramid can thus be determined in terms of the area of its various faces.

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills