How do Logarithms Work?

How do Logarithms Work?

Logarithms

“The Logarithm of a given number to a given base is the index of the power to which the base must be raised in order to equal the given number.”

If a > 0 and ≠ 1 then logarithm of a positive number N is defined as the index x of that power of ‘a’ which equals N i.e.,

It is also known as fundamental logarithmic identity.
Its domain is (0, ∞) and range is R. a is called the base of the logarithmic function.

When base is ‘e’ then the logarithmic function is called natural or Napierian logarithmic function and when base is 10, then it is called common logarithmic function.

Characteristic and mantissa

1. The integral part of a logarithm is called the characteristic and the fractional part is called mantissa.
   
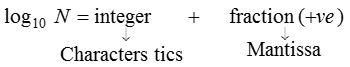
2. The mantissa part of log of a number is always kept positive.
3. If the characteristics of log₁₀ N be n, then the number of digits in N is (n+1).
4. If the characteristics of log₁₀ N be (– n) then there exists (n – 1) number of zeros after decimal part of N.

Properties of logarithms

Let m and n be arbitrary positive numbers such that a > 0, a ≠ 1, b > 0, b ≠ 1 then

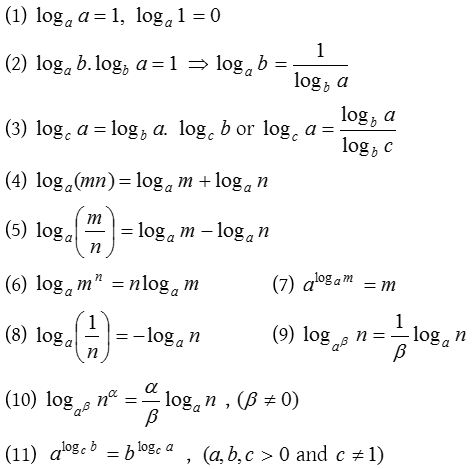
Logarithmic inequalities

(10) log _p a > log _p b ⇒ a ≥ b if base p is positive and >1 or a ≤ b if base p is positive and < 1 i.e., 0 < p < 1.
In other words, if base is greater than 1 then inequality remains same and if base is positive but less than 1 then the sign of inequality is reversed.