Kerala SSLC Maths Previous Question Papers with Answers 2018 are part of Kerala SSLC Maths Previous Year Question Papers with Answers. Here we have given Kerala SSLC Maths Previous Question Papers with Answers 2018.
| Board | SCERT |
| Class | SSLC Class 10 |
| Subject | Maths |
| Category | Kerala SSLC Previous Question Papers |
Kerala SSLC Maths Previous Year Question Papers with Answers 2018 Free Download English Medium
Time Allowed: 2 1/2 hours
Cool off time: 15 Minutes
Maximum Marks: 80
Instructions
- Read each question carefully before writing the answer.
- Give explanations wherever necessary.
- First 15 minutes is cool-off time.
- No need to simplify irrationals like √2, √3, π etc. using approximations unless you are asked to do so.
- Simplification of irrationals like √2, π, etc with their approximate values is not required it not specified on
the question.
Answer any 3 questions from I to 4. Each question carries 2 scores. (Scores 3 x 2 = 6)
Question 1.
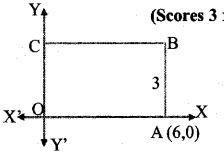
In the figure OABC is a rectangle and its breadth is 3. Write the Co-ordinates of the vertices B and C.
Question 2.
The letters of the word MALAYALAM are written in paper slips and put into a box. A child is asked to take
one slip from the box without looking.
a. What is the probability of getting the letter A?
b. What is the probability of not getting A?
Question 3.
The algebraic form of an arithmetic sequence is 5n +3.
a. What is the first form of the sequence?
b. What will be the remainder if the terms of the sequences are divided by 5?
Question 4.
The weights of 11 children in a school cricket club are 35, 39, 32, 36, 40, 30, 34, 37, 38, 33, 31 (kgs).
Find the median weight.
Answer any 5 questions from 5 to 11. Each question carries 3 scores. (Scores 5 x 3 = 15)
Question 5.
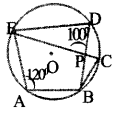
In the figure ‘0’ is the centre of the circle and A, B, C, D, E are the points on it ∠EAB = 1200, ∠EPD =100°. Write the measures of ∠EDB, ∠ECB and ∠DBC.
Question 6.
The algebraic form for the sum of first n terms of an arithmetic sequence is 2n2 + 8n. How many consecutive terms of the sequence, starting from the first, are to be added to get 330?
Question 7.
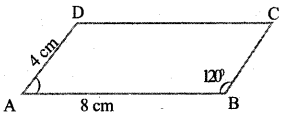
ABCD is a parallelogram. AB =8 cm, AD =4 cm, LB = 120°
a. What is ∠A
b. What is the perpendicular distance from D to AB?
c. What is the area of ABCD? A 8 cm B
Question 8.
Draw a circle of radius 3 cm. Mark a point 7 cm away from it’s centre. Draw the tangents to the circle from
this point.
Question 9.
The perimeter of the base of a square pyramid is 96 cm and its height is 16 cm.
a. What is the length of a base edge?
b. What is the slant height ?
c. Find the lateral surface area.
Question 10.
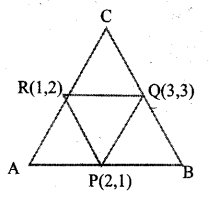
P, Q, R are the midpoints of the sides of the triangle ABC.
a. What type of the quadrilateral is PQCR ?
b. Write the Co-ordinates of the -vertices A and C.
Question 11.
P(x) is a second degree polynomial with P(1) = 0 and P (-2) = 0.
a. Find two first degree factors of P (x).
b. Find the polynomial P (x).
Answer any 7 questions from 12 to 21. Each question carries 4 scores. (Scores 7 x 4 = 28)
Question 12.
There are 20 terms is an arithmetic sequence. Sum of the first and last terms is 88.
a. What is the sum of the 2nd and 19th terms?
b. If 10th term is 42, what is the 11* term?
c. What is the common difference of the sequence ?
d. What is the first term ?
Question 13.
Draw a rectangle of length 4 em, breadth 3 cm and draw a square of the same Area.
Question 14.
There are 30 scouts and 20 guides in a school. In another school there are 20 scouts and guides. From each school, one student among them is to be selected for participation in a eminar.
a. What is the total number of possible selections ?
b. What is the probability of both being Scouts ?
c. What is the probability of both being Guides ?
d. What is the probability of one scout and one guide ?
Question 15.
‘O’ is die centre of the circumcircle of triangle ABC.
∠A = 40°,∠B = 80°, ∠C = 60°, BC = 6.4 cm.
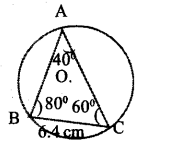
a. What is the diameter of the circle ?
b. What is the length of the other two sides ?

Question 16.
A circle with centre (3,2) passes through the point (6,3).
a. What is the radius of the circle ?
b. Check whether each of the points with coordinates (0,2), (3,6), (0,3) is inside, outside, or on the circle.
Question 17.
In the figure, the circle with centre ‘O’ is the excircle of the right triangle ACB g and P, Q, R are the points where the circle touches the sides of the triangle.
AC = 8 cm; CR = 4 cm; BR = 2 cm.
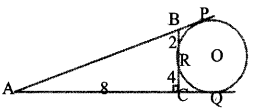
a. What is the length of AQ ?
b. What is the perimeter of the triangle ACB ?
c. What is the area of the triangle ACB ?
d. What is the radius of the incircle of triangle ACB ?
Question 18.
A circular sheet with radius 36 cm is divided into four equal sectors and one of them bent into a cone.
a. What is the slant height of the cone ?
b. What is the radius of the cone ?
c. What is the curved surface area ?
Question 19.
The coordinates of the vertices of a triangle are A (1, 1), i3 (5, 5), C (2, 5).
a. Write the co-ordinates of the midpoint D of AB.
b. What is the length of CD ?
c. What are the coordinates of the point dividing the line CD in the ratio 2:1?
Question 20.
P(x) = x3 + ax2 – x + b and
a. Find the relation between a and b for x -1 to be a factor of P(x).
b. Find the relation between a and b for x – 2 to be a factor of P(x).
c. Find a and b so that both x -1 and x – 2 are factors of P(x).
Question 21.
The table below shows the members in “Stree -Sakthi Kudambasree” sorted according to their ages.
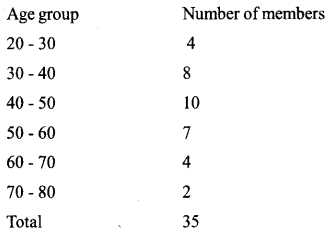
a. If the members are arranged in increasing order of ages, the age of the member at what position is taken as median ?
b. What is assumed to be age of the member at the 13 th position ?
c. Find the median of the ages.
Answer any 5 questions from 22 to 28. Each question carries 5 scores.
Question 22.
Consider the numbers between 100 and 300 which leave remainder 2 on division by 3.
a. Which is the first number in this sequence ?
b. Which is the last number in this sequence ?
c. How many such numbers are there in this sequence ?
d. Find the sum of all numbers in the sequence.
Question 23.
In the figure, the chord BD is perpendicular to the diameter AC. Find the measures of the following angles.
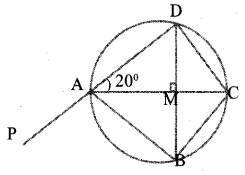
a. ∠ BAC
b. ∠ BCD
c. ∠ ADC
d. ∠ CDM
e. ∠ BAP
Question 24.
A rope of length 40 meters is cut into two pieces and two squares are made on the floor with them. The sum of the areas enclosed is 58 square meter.
a. If the length of one piece is taken as x, what is the length of the other piece ?
b. What are the lengths of the sides of the squares ?
c. Write the given fact about area as an algebraic equation.
d. What is the length of each piece ?
Question 25.
Draw a circle with radius 2.5 cm. Draw a triangle of two angles 50°, 60° with all its sides touching the circle.
Question 26.
A boy saw the top of a building under construction at an elevation of 30°. The completed building was 12 m higher and the boy saw its top at an elevation of 60° from the same spot.
a. Draw a rough figure based on the given details.
b. What is the height of the building ?
c. What is the distance between the building and the boy ?
Question 27.
The picture shows the shape of a boiler. Total height of the boiler is 12 m and the diameter is 6 meters, height of the cylindrical part is 6 meters.
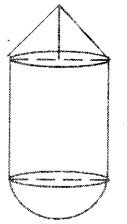
a. What is the height of the cone ?
b. How many litres can the boiler hold ? (1 m3 = 1000 litre)
Question 28.
A circle with centre (3, 4) passes through the origin.
a. What is the radius of the circle ?
b. If a point in the circle is (x, y), write the relation between x, y ?
c. Check whether the point (-2, 1) lie on this circle.
Question 29.
Read the following, understand the mathematical idea expressed in it and answer the questions that follow:
1,4,9,16, are the squares of the counting numbers. The remainders got by dividing the square numbers with natural numbers have a cyclic property. For example, the remainders on dividing these numbers by 4 are tabulated here.
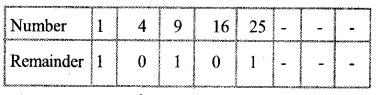
ANSWERS
Answer 1.
Given OABC is a rectangle
Breath = 3 cm
A(6,0)
From the figure AB=3 cm (breath)
Hence, B = (6,3)
C= (0,3) (OC = 3 cm breath)
Answer 2.
Given, the word ‘MALAYALAM’.
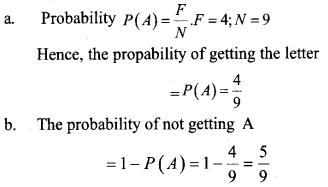
Answer 3.
Given, arithmetic sequence Xn = 5n + 3
a. The first term of the sequence, put n = 1
x1= 5 x 1 +3 = 8
b. d = 5 (coefficient of n be the common difference)
The remainder divided by 5 = 3.
(8/5 = 3, 13/5 = 3,18/5 = 3, etc)
Answer 4.
Given, the weight of the children
35, 39, 32, 36, 40, 30, 34, 37, 38, 33, 31
Arrange the data in assenting order
30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40
Median = 35. (the middle number)
Answer 5.
Given, ∠EAB = 120°∠EPD = 100° ∠EDB = 60° (ABCD is a cyclic quadrilateral, opposite angles are supplementary, 180 120=60°)
∠ECB = 60° -(Same arc angle equal)
In ABPC, ∠C = 60, ∠P = 100
∠B = 180 – (100 + 60) = 20°
ie., ∠DBC = 20°
Answer 6.
Given, the sum of the first n terms of an arithmetic sequence = 2n2 + 8n
ie., 2n2 + 8n = 330
⇒ In2 = 8n – 330 = 0 dividing by 2
⇒ n2 4n – 165 = 0 factorize
⇒ (n + 15 ) (n – 11) = 0
ie., n+15 =0 or n-11 = 0
n = -15 or n = 11; -15 rejected
n = 11
ie., the sum of the first n number be 11.
Answer 7.
Given ABCD is parallelogram, AB = 8cm, AD = 4cm, ∠B = 120°

a. ∠B = ∠D =120°
(opposite angles equal)
∠A + ∠C = 360-(120 + 120)
= 360-240 = 12
∴ ∠A = ∠C = \(\frac { 120 }{ 2 }\) = 60
∴ ∠A= 60°
b. Draw DE as perpendicular from D to AB. From the figure
DE = 2√3 cm. [1: √3 : 2]
c. The area of ABCD = bh (formula)
= 8 x 2 √3 = √3 cm2
Answer 8.
Given radius = 3 cm,
Distance from the center = 7 cm.
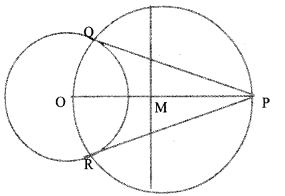
Construction.
Draw a circle 3 cm radius and O as its center. From center mark OP=7cm. Draw perpendicular bisector of the line OP and meet M.Draw a circle with radius OM and cut the circle at Q and R. Joint PR and PQ. Hence, PR and PQ are the tangents.
Answer 9.
Given, perimeter of the Pyramid = 96 cm
Height = 16 cm
a. 4a= 96
a =\(\frac { 96 }{ 4 }\) = 24 cm(side)
∴ Base edge = 24 cm
b. Slant height (1)
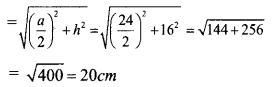
c. Lateral surface area (LSA) = 2al
= 2 x 24 x 20 = 960 cm2
Answer 10.
a. From the figure, PQCR be a Parallelogram
b. From the figure, we can see that If PQCR is a parallelogram, then cordinate of C is (2,4).
Also APQR is a parallelogram cordinate of A= (0,0)
Answer 11.
Given, P(l) = 0 and P (-2) = 0
First degree factors = (x -1) (x + 2)
(using factor theorem)
b. P(x) = (x-1) (x + 2) = x2+ x – 2
Answer 12.
Given n = 20
Sum of the first and last term =88
a. The sum of the 2nd and 19th terms
ie., x2 + x19= x1 + d + x20– d = x, + x20 = 88.
b. Given 10th term 42.
x10+ x11 = (x1+ 9d) + (x20– 9d)
ie.,42 + x11= x1 + x20
∴ x11 = x11 + x20– 42 = 88 – 42 = 46
Hence 11th term = 46
c. Common difference (d) = x11 = x10 = 46 – 42 = 4
d. The first term
x1 = x1+ 9d = 42 (given 10th term 42)
= 42 – 9d = 12 – 9 x 4 = 6
Hence the first term = 6
Answer 13.
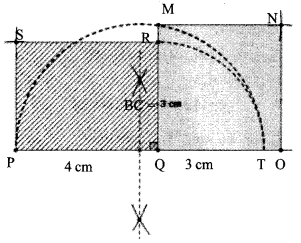
Draw a rectangle PQRS in the given measurement. PQ produced up to T as QT = 3 cm. Draw a perpendicular bisector of the lime PT, meet Q on PT. Produce QR meet the semicircle at M. Draw the square QMNO as QM = MN = ON = QO. Hence QMNO be the required square.
Answer 14.
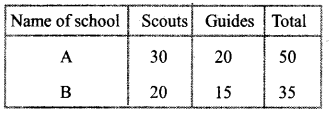
Total number of possible selection = m x n
(fundamental counting theorem)
a. m x n =50 x 35 = 1750
b. Probability of both being scouts

Answer 15.
Given √4 = 40°, √B = 80°’√60°,BC = 64 cm
![]()
b. Side AC= d x sin B= 10 x sin 80
= 10 x 0.98 = 9.8 cm.
c. Side AB = d x sin C= 10 x sin 60
= 10 x 0.87 = 8.7 cm.
Answer 16.
a. Given points (3,2) and (6,3) (Using the distance formula)
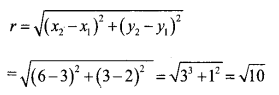
b. (3,2) and (0,2) (Using the distance formula)
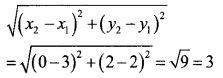
Here 3 is less than the radius, so the point is inside the circle.
(3, 2) and (3, 6) (Using the distance formula)
![]()
Here 4 is greater than the radius, so the point be outside the circle.
(3, 2) and (0, 3) (Using the distance formula)
![]()
Here √10 is equal to the radius, so the point be on the circle.
Answer 17.
Given, AC= 8 cm, CR= 4 cm, BR=2 cm
a. Length of AQ. From the figure,
AQ = AC + CQ = AC+ (CR = CQ)
(tangents are equal) = 8 + 4 = 12 cm.
∴ AQ =12 cm.
b. Perimeter of the ΔACB,
ΔACB is a right angled triangle, by Pythagoras,
AB2 = AC2 + BC2
AC=8 cm, BC = CR + RB = 4 + 2 = 6
ie., AB2 = 82+ 62 = 64 + 36 = 100
AB = √100 = 10 cm.
Hence the perimeter = 8 + 6 + 10 = 24 cm
c. Area of the ΔACB=1/2 x bh = 1/2 x 8 x 6 = 24cm2.
d. Radius of the in-circle of ΔACB
![]()
Answer 18.
Radius of the circular sheet 36 cm
a. Slant height of the cone =36 cm
b. Radius of the cone, r = \(\frac { r }{ 1 }\) =\(\frac { x }{ 36 }\) ( formula)
Centre angel (x) = 360/4=90°.
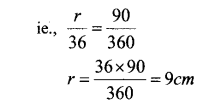
Hence, the radius of the cone = 9 cm
c. Curved surface area (CSA) = πrl
= π x 9 x 36 = 324 π cm 2
= 324 x 3.14 = 1017.36 cm2
Answer 19.
Given, the vertices of the Δ ABC, A (1, 1), B (5, 5), C (2, 5)

Answer 20.
Given P(x) = x3 + ax2 – x + b
a. x-2 is a factor of p(x)
ie., P(1) = 0
ie., P(1) = (1)3+ ax (1)2– 1 + b = 0
= 1 + a- 1+b = 0;a + b = 0.
b. x-2 is a factor of P(x)
ie., P(2) =0
So, P(2) = 23 + a x 22 – 2+ b = 0
= 8 + 4a-2 + b = 0
= 4a + b = -6.
c. We have, a + b = 0 and 4a + b = -6.
Solve this two equation.
We get a = -2 and b = 2.
Answer 21.
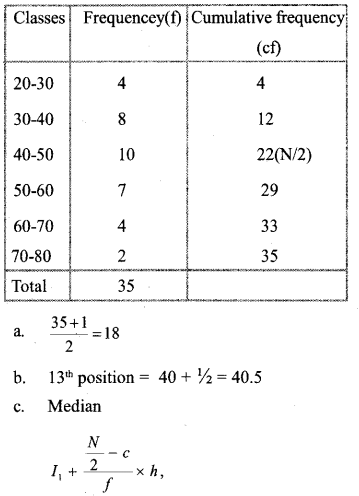
l1 = lower limite of the median class.
N = Total number of frequencies,
c = Above the cf of the median class.
f= frequency of the median class,
h= class interval
N/2 = 35/2= 17.5.
Median class = 40-50. (N/2=1 7.5 included class)
I1+40, c =12, f=10
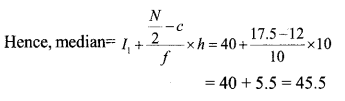
Answer 22.
Numbers b/w 100 and 300 which leave remainder 2 on division by 3 First term =99 + 2= 101., d = 3 So, the sequence be 101,104,107,110…… 299 last term =300-1=299.
a. The first term=101
b. Last term =299.
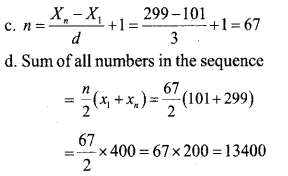
Answer 23.
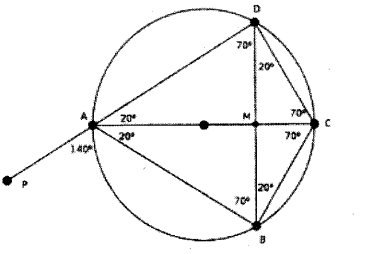
∠B AC = ∠CAD= 20°
∠BCD = 140°.
(180-40 =140, cyclic quadrilateral)
∠ADC = 90° (angle of the semicircle)
∠CDM = ∠B AC – 20°
(angle in the same arc).
∠BAP = 140°. (180-40 = 140, linear pair)
Answer 24.
Length of the rope = 40cm Let length of the one piece = x
a. Length of the other piece = 40 – x
b. Length of the sids of the square

c. The algebraic form, Given, sum of the area
= 58cm2.
ie., a2+ a2= 58 cm2.
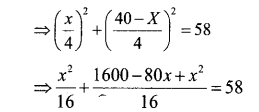
⇒ 2x2 – 80x + 1600 = 58 x 16
⇒ 1x2 – 80x + 1600 = 928
dividing throught out by 2,
ie., x2 – 40x + 800 = 464.
⇒ x2-40x +800-464 = 0
⇒ x2 — 40x + 336 = 0
Length of each piece,
x2-40 x 336 = 0 (factorize)
⇒ (x – 28) (x -12) = 0
⇒ x-28 = 0 or x-12 = 0
x = 28 or x= 12.
The length of each pieces = 28 m or 12 m.
Answer 25.
The length of each pieces = 28 m or 12 m. 25. Draw a circle radius 2.5 cm with center O. Draw Om as radius
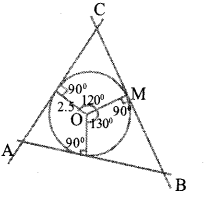
∠MON = 120° and ∠MOP = 100°. Draw the tangents through M,N and P respectively and meet at A, B and C. ΔABC be the required triangle.
Answer 26.
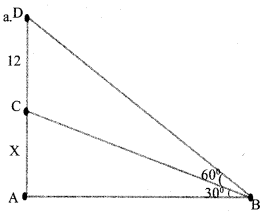

Answer 27.
Given, total height=12m
Radius = 6/2=3m
Height of the cylinder part (h)=6m
a. Height of the cone= 12-(6+3) = 3m
b. Volume of the boiler
= Volume of the cone + volume of the cylinder + volume of the hemisphere.
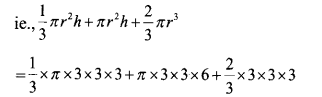
= 9 π + 54 π +18π =81π m3
= 81 x 3.14 = 254.34m3.
Hence, the volume in liters
= 254.34 x 1000 = 254340 liters.
Answer 28.
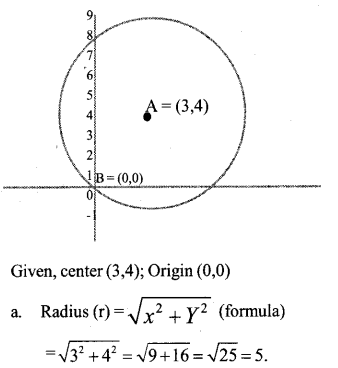
b. Equation of the circle
= (x – a)2 + (y – b)2 = r2.
ie., (x – 3)2+ (y – 4)2= 52.
⇒ x2 – 6x + 9 + y2 – 8y + 16 = 25
⇒ x2 + y2 – 6x – 8y + 25 – 25 = 0
⇒ x2 + y2 – 6x – 8y = 0
be the equation of the circle,
c. (-2, 1), put this value in the equation
we get, (-2)2+(1)2– 6x – 2 – 8 x 1 = 0
4+1 + 12-8 = 0
17 – 8 = 0
9 ≠ 0.
Hence, the point (-2, 1) is not lies on the circle.
Answer 29.
a. 0,1 and 3.
b. 2 and 3
c. 2,1,0 and 3.
d. No. 3,7,11,……………. is divided by 4 we get the remainder 3. When we dividing the perfect square numbers by 4, we get the remainer 0 and 1.
e. 4,8,12,16……………
We hope the Kerala SSLC Maths Previous Question Papers with Answers 2018 help you. If you have any query regarding Kerala SSLC Maths Previous Question Papers with Answers 2018, drop a comment below and we will get back to you at the earliest.