Kerala SSLC Maths Model Question Papers with Answers Paper 1 are part of Kerala SSLC Maths Previous Year Question Papers with Answers. Here we have given Kerala SSLC Maths Model Question Papers with Answers Paper 1.
| Board | SCERT |
| Class | SSLC Class 10 |
| Subject | Maths |
| Category | Kerala SSLC Previous Question Papers |
Kerala SSLC Maths Model Question Papers with Answers Paper 1 Free Download English Medium
Time Allowed: 2 1/2 hours
Cool off time: 15 Minutes
Maximum Marks: 80
Instructions
- Read each question carefully before writing the answer.
- Give explanations wherever necessary.
- First 15 minutes is cool-off time.
- No need to simplify irrationals like √2, √3, π etc. using approximations unless you are asked to do so.
- Simplification of irrationals like √2, π, etc with their approximate values is not required it not specified on
the question.
Answer any 3 questions from 1 to 4. Each question carries 2 scores. (Scores 3 x 2 = 6)
Question 1.
In the figure , if AB = 4m and AC = 8m, then find the angle of elevation of A as obseved from C.
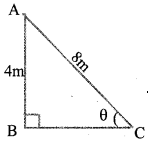
Question 2.
In the figure, the sides of the rectangle ABCD and PQRS are parallel to the axes. Find the coordinates of the vertices of all the rectangles in it.
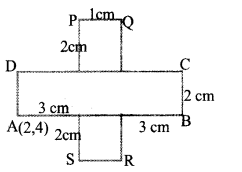
Question 3.
The first term of an arithmetic sequence is 2 and common difference is 3. Is 100 a term of this sequence ? Why ?
Question 4.
Number of members in 10 families, collected by mathematics club survey are given. Calculate median?
4, 2, 3, 5, 4, 3, 2, 20 ,4, 3
Answer any 5 questions from 5 to 11. Each question carries 3 scores. (Scores 5 x 3 = 15)
Question 5.
A triangle and its circum circle are shown in the picture.
(a) Find ∠AOB ?
(b) Find the diameter of circle?
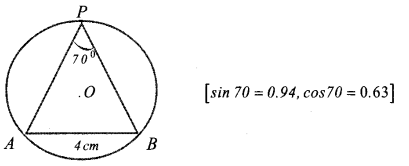
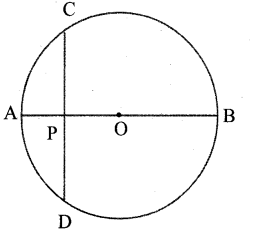
Question 6.
In the figure, AB is a diameter of the circle and the chord CD is perpendicular to AB. If CD = 4 √5 centimetres and PA = 2 centimeters, find AB.
Question 7.
The sum of two numbers is 15. If the sum of their reciprocals is 3/10. Find the numbers.
Question 8.
How many three-digit numbers are there, which leave a remainder 3 on division by 7 ?
Question 9.
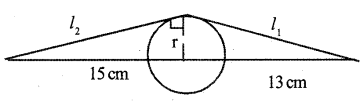
If a point is marked at a distance 13 cm from the centre of a circle and a tangent of length 5 cm is drawn from this point to the circle, then find the length of the tangent from the point which is 15 cm apart from the centre of the same circle.
Question 10.
See these figures made with matchsticks:
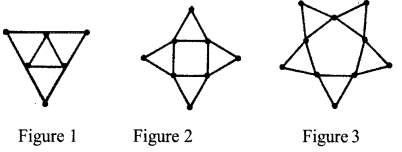
a. How many sticks are needed for the next figure?
b. If we continue this, what is the relation betwen the number’s 1,2,3…. and the number of matchsticks used in Figure 1, Figure2, Figure 3 and so on?
c. If we write the number of matchsticks in order, what is the algebraic expression to find the n,h term of this sequence?
Question 11.
In the figure below, ABCD is a parallelogram. The lines AP and DQ are parallel to the x-axis and the lines BP and CQ are parallel to the y-axis.
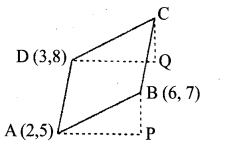
a. What are the lengths of AP and BP?
b. What are the lengths of DQ and CQ?
e. What are the coordinates of C?
Answer any 7 questions from 12 to 21. Each question carries 4 scores. (Scores 7 x 4 = 28)
Question 12.
Two dice, each marked with numbers from 1 to 6, are rolled together:
a. If the possible numbers got from the dice are written as pairs, how many pairs would be there?
b. In how many pairs are the product of the numbers odd?
c. What is the probability of getting an odd product?
c. What is the probability of getting an even product?
Question 13.
In the figure below, AB and AC are chords of the circle and OP and OQ are radii parallel to them:
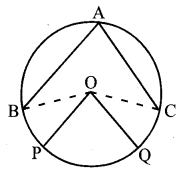
a. What is the relation between ∠BOC and ∠POQ ?
b. What is the relation between the small arc joining B and C the small arc joining P and Q?
Question 14.
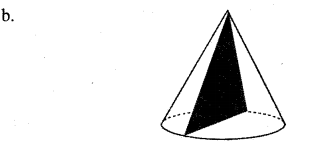
A cone is made by bending a semicircle.
a. What is the relation between its base radius and slant height?
Question 15.
The daily wages of people working in different fields in a company are given below.
| Wages (in Rs.) | No. of Workers. |
| 200 – 250 | 2 |
| 250 – 300 | 5 |
| 300 – 350 | 8 |
| 350 – 400 | 10 |
| 400 – 450 | 7 |
| 450 – 500 | 5 |
| 500 – 550 | 4 |
Determine the median wages of the workers.
Question 16.
i. A straight line intersect co-ordinate axis at (a, 0) and (0, b).
Prove that the equation of this straight line is \(\frac { x }{ a } +\frac { y }{ b } \)= 1.
ii. The line \(\frac { x }{ 6 } +\frac { y }{ 4 } \) = 1 cuts the x-axis at point A and y-axis at point B. Write the co-ordinates of A and B.
iii. Prove that the point (3, 2) is lies on the line \(\frac { x }{ 6 } +\frac { y }{ 4 } \) = 1
Question 17.
A man standing on level ground sees the top of a far away hill at an elevation of 70°. Moving 100 meters back, he sees it at an elevation of 50°. Taking tan 70° ≈ 2.8 and tan 50° ≈ 1.2 find the approximate height of the hill.
Question 18.
The table below shows groups of children in a class according to their heights:
| Height (cm) | Number of Children |
| 135 – 140 | 5 |
| 140 – 145 | 8 |
| 145 – 150 | 10 |
| 150 – 155 | 9 |
| 155 – 160 | 6 |
| 160 – 165 | 3 |
a. If the children are lined up according to their heights, the median is the height of the child in which position?
b. According to the table, the height of this child is between what limits?
c. What are the assumptions used to compute the median?
d. What is the median height according to these assumptions?
Question 19.
The figure below shows two parallel sides of a square extended by 4 centimeters to make a rectangle:
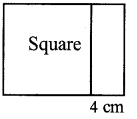
The area of the new rectangle is 396 square centimeters.
a. Taking the length of a side of the square as x centimeters, write down the given facts as an algebraic equation
b. Using this equation, compute the length of a side of the square.
Question 20.
In the figure below, P,Q, R are the points where the incircle of Δ ABC touches the sides:
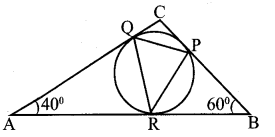
a. Compute the other two angles of ΔAQR.
b. Compute the angle at P in APQR.
c. Compute the other two angles of APQR.
Question 21.
All four digit numbers are formed using the digits 1,2,3,4 (Assuming no repetitions) and each number is written in a paper and put in a box. Take a paper without looking into the box.
a. What is the probability that it is an odd number ?
b. What is the probabality that it is a multiple of 4. ?
Answer any 5 questions from 22 to 28. Each question carries 5 scores.
Question 22.
A man whose height is 1.5 m standing on the top of a big building observes that angles of depression of the top and bottom of a small building to be 35° and 75°. The height of the small building is 15 m.
i. Draw a rough figure and mark the given measurements.
ii. Find height of the big building.
iii. Find the distance between two buildings,
tan 35° = 0.7 tan 75° = 3.73
sin 35° = 0.573 sin 75° = 0.965
cos 35° = 0.82 cos 75° = 0.258
Question 23.
If x2 – 4 is the factor of a polynomial ax3 + bx2 + cx + d then,
i. Prove that
\(\frac { d-c }{ a-b } =4\)
ii. A first – degree binomial is to be added with the polynomial 2x3 – 3x2 – 10 x + 7 such that the sum is the polynomial with factor x2 – 4.
Question 24.
Draw a rectangle of width 5 centimetres and height 3 centimetres. Draw a rectangle of the same area with width 6 centimetres.
Question 25.
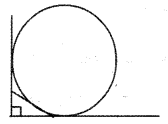
In figure, mutually perpendicular tangents and one another tangents can make a triangle. Prove that perimeter of the triangle is equal to the diameter of the circle.
Question 26.
Cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base. Compare the volume of the two parts.
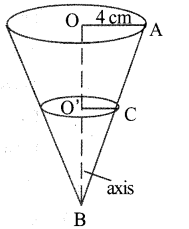
Question 27.
A man saved Rs. 16,500 10 years. In each year after the first he saved Rs.100 more than he did in the preceding year. How much did he save in the first year.
Question 28.
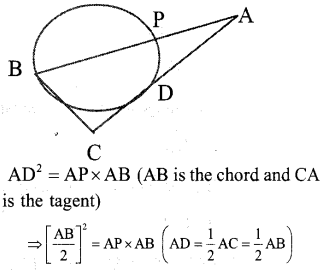
ABC is an isosceles triangle with AB = AC. A circle through B touches side AC at its middle point D and intersect side AB in point P. Show that AB = 4 x AP
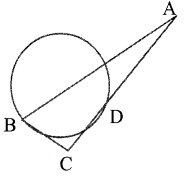
Question 29.
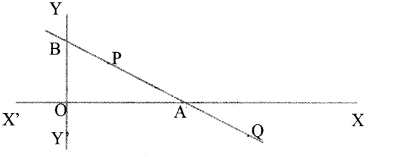
In the figure, equation of the line joining the points A and B is x + 2y = 10. P and Q are points on this line.
a. Find the coordinates of the points A and B.
b. Find the coordinates of the point P that divides the line AB in the ratio 2 : 3.
c. If AQ : BQ = 2:3, find the coordinates of the point Q.
ANSWERS
Answer 1.

Answer 2.
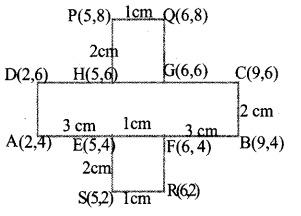
Answer 3.
First term = 2 = a + b
Common difference a = 3
b = 2 – 3 = -1
xn = an + b= 100
3n – 1 = 100
3n = 101
n = 33.6
∴ 100 is not a term in the AP, because n is not a natural number.
Answer 4.
Arrange the data in assenting order 2, 2, 3, 3, 3, 4, 4, 4, 5, 20 Median =
\(\frac { 3+4 }{ 2 } =3.5\)
Answer 5.
(a) ∠AOB = 70 x 2 = 140
(b) Length of side AB = 2r sin 70
4 = dsin 70
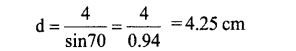
Answer 6.
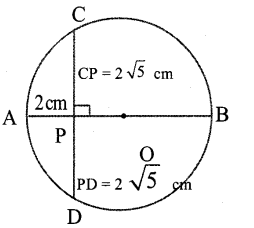
CD = √5
CP = PD = 2 √5 cm
AP x PB = PC2
2 x PB = (2 √5 )2
PB = 10 cm
Diameter of the sphere
AB = AP + PB
= 2+ 10= 12 cm
Answer 7.
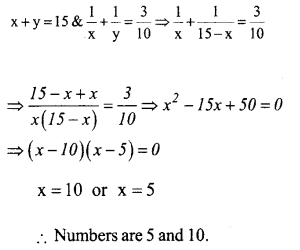
Answer 8.
101,108,115………..,997
Number of three digits which leave a remainder 3 on division by 7
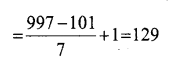
Answer 9.

Answer 10.
a. Sequence of the given sticks are 9,12,15…
∴ Number of sticks are needed for the next figure is 15 + 3 = 18
b. The number of sticks used for making the figures is 6 added to 3 times the numbers of the sequence 1, 2, 3, 4
c. Forthe sequence 9, 12, 15…….
xa = dn+(x,-d)
= 3n + (9 – 3) = 3n + 6
Answer 11.
In the right angled triangle Δ APB and right angled triangle Δ DQC, the hypotenuse and one side are equal so the triangles are similar.
x coordinate of P in the figure = 6
y coordinate of P in the figure = 5
∴ Coordinates of P = (6, 5)
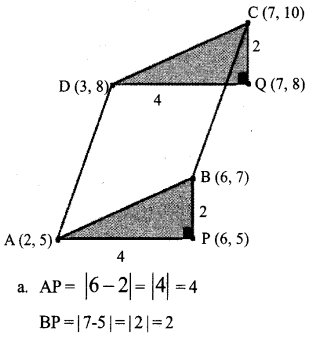
b. Right angled triangle A APB and right angled triangle Δ DQC are similar triangles. So, DQ = 4, CQ = 2 (Similar sides are equal)
c. y coordinate of Q = x coordinate of D + 4 = 3 + 4 = 7
y coordinate of Q = y coordinate of D = 8
∴ Coordinates of Q = (7, 8)
∴ x coordinates of C = x coordinates of Q = 7
y coordinates of C = y coordinates of
Q + 2 = 8 + 2 = 10
∴ Coordinates of C = (7, 10)
Answer 12.
a. Total numbers on a dice = 6
Total numbers on a another dice = 6
Total number of pairs possible = 6 x 6 = 36
b. (1, 1), (1 ,3), (1 ,5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)
There are 9 pairs
c. Probability of getting product as odd =
\(\frac { 9 }{ 36 } =\frac { 1 }{ 4 } \)
d. Probability of getting product as even
= Total probability
\(\frac { -1 }{ 4 } =1-\frac { 1 }{ 4 } =\frac { 3 }{ 4 } \)
Answer 13.
a. AB is parallel to OP and AC is parallel to OQ, then
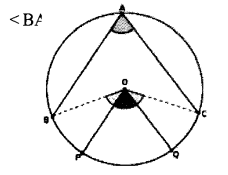
∠BOC = 2x ∠BAC
∠B AC = ∠POQ
∴ ∠BOC = 2x ∠POQ
i.e., ∠BOC is two times of ∠POQ.
b. Let ∠POQ = x and r be the radius of the circle then
∠BOC= 2 x ∴ length of small arc PQ.
= 2πr x (x/360)
∠BOC = 2 x length of small arc BC
= 2 nr x (2x / 360)
= 2 x length of small arc PQ
i.e., Length of small arc BC
= 2 x length of small arc PQ.
Answer 14.
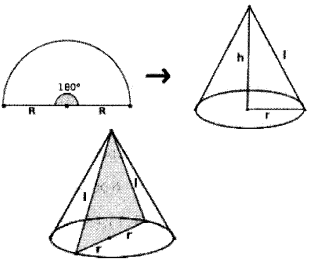
a. Length of arc in the hemisphere = Base perimeter of cylinder.
∴ 2π R x (180/360) = 2πr
∴ 2π R x (1/2) = 2πr
∴ R = 2r,
∴ 1 = 2r
(i.e., slant height = base radius) or r = 1/2
Ratio of base radius and slant height = 1:2
b. The sides of the triangles are base diameter and slant heights.
Here slant height = 2r = diameter Hence all sides of the triangle are equal and it is an equilateral triangle
Answer 15.
Total number of workers = 41
The wages of 21st worker is the median
Median class: 350 – 400 ⇒ 10
Wages of 10 workers 352 1/2., 357 1/2, 362 1/2.……….are in A.P
6th term of AP = 352 1/2, + 5 x 5 = 377 1/2
Answer 16.
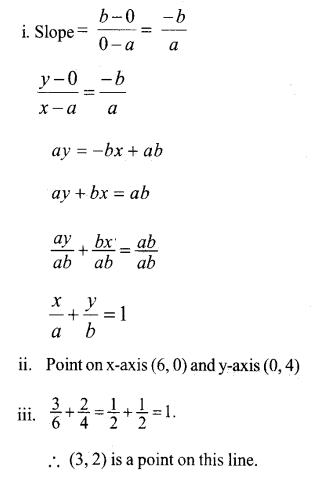
Answer 17.
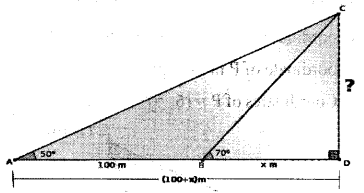
Let the height of the hill be CD and height of the tower be PQ. Let B be is the first position of the man who watch the hill and A be the second position which is 100 m behind B, CD is to be calculated.
∠DBC = 70°, ∠DAC = 50°(Given)
AB = 100 m (Given)
Let BD = x m
AD = (100 + x) m
In right angled triangle
Δ CBD tan 70 = CD / BD
2.8 = CD/x
∴ CD = 2.8 x ……………..(1)
CD and AD belongs to the right angled Δ CBD.
tan 50 = CD/AD 1.2 = CD/(100 + x)
1.2 x (100+x) = CD
(1.2 x 100) + (1.2 x x) = CD
(1.2 x 100) + (1.2 x x) = CD
120+ 1.2 x = CD………………(2)
Sub (2) in (1)
120+1.2x = 2.8x
2.8x- 1.2x = 120 1.6x= 120
x= 120/1.6= 1200/16 = 75
Substitute x = 75 in equation (1), the height
of hill = CD = 2.8 x = 2 – 8 x 75 = 210 m
Answer 18.
| Height (cm) | Number of Children |
| Below 140 | 5 |
| Below 145 | 13 |
| Below 150 | 23 |
| Below 155 | 32 |
| Below 160 | 38 |
| Below 165 | 41 |
a. Height of the 21st child is the median height.
b. Height of the 21st child is between 145 cm and 150 cm.
c. Methods to find the madian are
- Divide 5 cm in between 145 cm and 150 cm into 10 equal sect-ions.
- Consider that the height of each sub-group is exactly on the mid point of the subgroup.
d. Height of the 14th child is in between 145 cm and 145 5/10 cm. i.e., 145 5/20 cm.
Similarly, the height of the 15th student is in between 145 5/10 cm and 145 10/10 cm i.e., 145 1 5/20 cm.
Hence height of each child can be increased by 5/10 cm.
There are 7 children to reach the 21st child from 14th child, i.e., 14th term is 145 5/20 and common difference is 5/10.
Mean is the 21 st term of the arithmetic sequence.
∴ Mean height = x21 = x14 + 7d
= 145+5/20+ (7 x 5/10)
= 145+5/20+35/10
= 145+5/20+70/20
= 145+75/20= 145 +3 15/20
= 145 + 3+15/20
= 148 15/20=148.75
Answer 19.
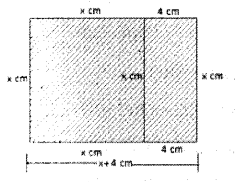
a. Let x cm be the length of the square then the length of the new square
= (x +4) cm, Width = x cm
Area of the new square= 396 cm2
(Given)
∴ Width x length = 396
x (x + 4) 396
x2 + 4x = 396
b. x2 + 4x = 396
According to the complete square method
x2 + 4x + 4 = 396 + 4
i.e., (x + 2)2=400
x + 2 = ±√400
∴ x + 2 = 20 or x + 2 = -20
x = 20-2 or x = -20-2
x = 18 or x = -22
One side of square cannot be negative
Hence one side of the square= 18 cm
Answer 20.
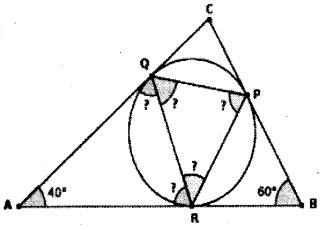
a. Tangents from a point outside a circle have same length.
AQ = AR, BR= BP, CP = CQ AQ = AR
∴ Δ AQR is an isosceles triangle.
In A AQR, ∠QAR = 40°
∠AQR = ∠ARQ
= (180-40)/2 = 140/2=70°
b. Angles made by chord and tangents are equal to the angle of alternate arc.
∠AQR = 70°
In Δ PQR, ∠p = 70°
c. Since BR = BP
∴ Δ BRP is an isosceles; triangle.
In Δ BPR, ∠RBP = 60° ∠BRP = ∠BPR
= (180 – 60)/2 = 120/2 = 60°
Angles made by chord and tan¬gents are equal to the angle of alternate arc.
∠BRP = 70°
In ΔPQR ∠Q = 60°
Sum of angles of a triangle is 180°, then
∠R=180
(∠P + ∠Q) =180-(70 + 60) =180 – 130 = 50° Other angles of Δ PQR is 60° and 50°
Answer 21.
Total sample space

Answer 22.
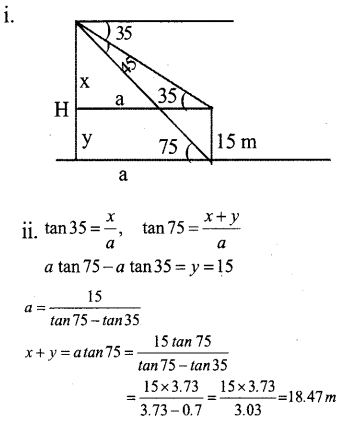
Height of tall building
a = 18.47 – 1.5 = 16.97 m
iii. distance between two building,
a = \(\frac { 15 }{ 4.95 m } =4\)
Answer 23.
i. P(2) = 8a + 4b + 2c + d = O
p (-2)= – 8a + 4b – 2c + d = O
8b + 2d = O = 4b ÷ d = O
8a + 2c = O = 4a + c = O
d – c = 4a – 4b
\(\frac { d-c }{ a-b } =4\)
ii. Let the first degree binomial be px + q
2x3 – 3x2 – 10x + 7 + px + q.
d = -4b 7 + q = -4 x -3 = 12
q = 5
c = -4a ⇒ -10 + p = -8, p = 2
px + 2 = 2x + 5
Answer 24.
ABCD, is a rectangle of length 5 cm and width 4 cm.
Area= 20 cm2
AGFE, is a rectangle of length 6 cm and
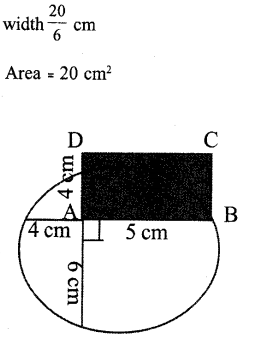
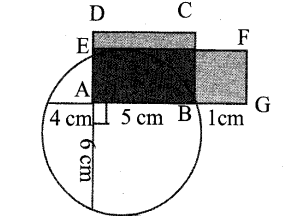
Answer 25.
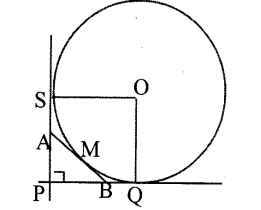
O is the centre of the circle and OS perpendicular to OS
(Radius is perpendicular to tangent)
OQ perpendicular PQ
(Radius is perpendicular to tangent)
OS = PS = PQ = OQ (PQRS is a square)
PS = PA + AS
AS = AM (tangent from A are equal)
PS = PB + BQ
BM = BQ (tangent from B are equal)
PQ = PB + BM
∴ PS + PQ= PA+AM + PB + BM
= PA+ PB + AM + BM
= PA+PB+AB
= Perimeter of triangle
PS+ PQ is the diameter of circle.
∴ The perimeter of the triangle is equal to the diameter of the circle.
Answer 26.
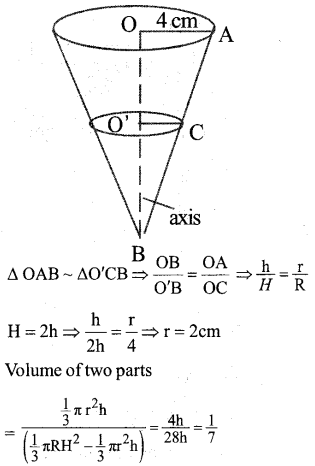
Answer 27.
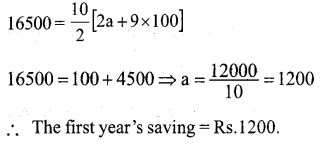
Answer 28.
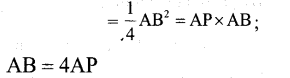
Answer 29.


We hope the Kerala SSLC Maths Model Question Papers with Answers Paper 1 help you. If you have any query regarding Kerala SSLC Maths Model Question Papers with Answers Paper 1, drop a comment below and we will get back to you at the earliest.