ISC Physics Question Paper 2019 Solved for Class 12

ISC Physics Previous Year Question Paper 2019 Solved for Class 12

Maximum Marks: 70
Time allowed: Three hours

• Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.
  All questions are compulsory.
• This question paper is divided into 4 Sections, A, B, C and D as follows :
• Section A: Question number 1 is of twelve marks. All parts of this question are compulsory.
• Section B: Question numbers 2 to 12 carry 2 marks each with two questions having internal choice.
• Section C: Question numbers 13 to 19 carry 3 marks each with two questions having internal choice.
• Section D: Question numbers 20 to 22 are long-answer type questions and carry 5 marks each.
• Each question has an internal choice.
• The intended marks for questions are given in brackets [ ].
• All working, including rough work, should be done on the same sheet as and adjacent to the rest of the answer.
• Answers to sub parts of the same question must be given in one place only.
• A list of useful physical constants is given at the end of this paper.
• A simple scientific calculator without a programmable memory may be used for calculations

Section – A
Answer all questions.

Question 1.
(A) Choose the correct alternative (a), (b). (c) or (d) for each of the questions given below : [5 × 1]
(i) A closed surface in vacuum encloses charges -q and +3 q. The total electric flux emerging out of the surface is :
(a) Zero
(b) \(\frac{2 q}{\epsilon_{o}}\)
(c) \(\frac{3 q}{\epsilon_{0}}\)
(d) \(\frac{4 q}{\epsilon_{0}}\)

(ii). What is the angle of dip at a place where the horizontal component (B_H) and vertical component (B_V) of earth’s magnetic field are equal:
(a) 130°
(b) 60°
(c) 45°
(d) 90°

(iii). A beam of light is incident at the polarizing angle of 35° on a certain glass plate. The refractive index of the glass plate is :
(a) sin 35°
(b) tan 35°
(c) tan 55°
(d) sin 55°

(iv). In a gamma ray emission from nucleus :
(a) only the number of protons change.
(b) the number of protons and neutrons, both change.
(c) there is no change in the number of protons and the number of neutrons.
(d) only the number of neutrons change

(v). The energy associated with light of which of the following colours is minimum
(a) violet
(h) red
(c) green
(d) yellow

(B) Answer the following questions briefly and to the point. [7 × 1]
(i) Define equipotential surface.
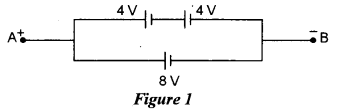
(ii) Calculate the net emf across A and B shown in Figure 1 below :

(iiii) Why are the pole pieces of a horseshoe magnet in a moving coil galvanometer made cylindrical in shape ?
(iv) What is the value of power factor for a pure resistor connected to an alternating current source ?
(v) What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment.
(vi) Define critical angle for a given medium.
(vii) Name the series in the atomic spectra of the hydrogen atom that falls in the ultraviolet region.
Answer:
(A) (i) (b)
(ii) (c)
(iii) (b)
(iv) (c)
(v)(a)

(B) (i) An equipotential surface is one on the surface of which the potential is same.
(ii) 8V
(iii) This is done to produce a radial magnetic field.
(iv) one.
(v) zero.
(vi) It is defined as the angle of incidence in the denser medium for which the angle of refraction in the rarer medium is 90°.
(vii) Lyman series.

Section – B
Answer all questions.

Question 2. [2]
In a potentiometer experiment, the balancing length with a resistance of 2 Ω is found to be 100 cm, while that of an unknown resistance is 500 cm. Calculate the value of the unknown resistance.
Answer:
Given R₁ =2Ω ,L₁ = 100 cm, L₂= 500 cm, R₂ = ?
Using the expression \(\frac{E_{2}}{E_{1}}=\frac{L_{2}}{L_{1}}=\frac{R_{2}}{R_{1}} \Rightarrow R_{2}=\frac{L_{2} R_{1}}{L_{1}}=\frac{500 \times 2}{100}=10 \Omega\)

Question 3. [2]
A rectangular loop of area 5 m^H. has 50 turns and carries a current of 1 A. It is held in a uniform magnetic field of 0. IT, at an angle of 30°. Calculate the torque experienced by the coil.
Answer:
Given, A= 5 m2, n = 50, I = 1 A, B = 0.1T, θ= 30°, T= T
\(\mathrm{T}=\mathrm{B} \ln \mathrm{A} \sin \theta=0.1 \times 1 \times 50 \times 5 \times \sin 30^{\circ}=12.5 \mathrm{Nm}\)

Question 4. [2]
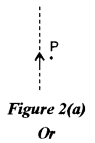
(a) A electric current I flows through an infinitely long conductor as shown in Figure 2(a) below. Write an expression and direction for the magnetic field at point P.

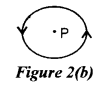
(b) An electric current I flows through a circular loop as shown in Figure 2(b) below. Write an expression and direction for the magnetic field at the centre of the loop at point P.

Answer:
\(\mathrm{B}=\frac{\mu_{0} \mathrm{I}}{2 \pi r}\) , perpendicular to the plane of the paper and directed inwards.
\(\mathrm{B}=\frac{\mu_{0} \mathrm{I}}{2 r}\) , perpendicular to the plane of the paper and directed outwards.

Question 5. [2]
A transformer is used to step up an alternating emf of 200 V to 440 V. If the primary coil has 1000 turns, calculate the number of turns in the secondary coil.
Answer:

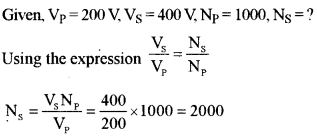
Question 6. [2]
State any two properties of microwaves.
Answer:

• They move with the speed of light.
• They can heat matter.

Question 7. [2]
Write any one use for each of the following mirrors :
(a) Convex
(b) Concave
Answer:
(a) Used as a rear view mirror.
(b) Used as a shaving mirror.

Question 8. [2]
The deviation produced for violet, yellow and red lights for crown glass are 3.75°. 3.25° and 2.86° respectively. Calculate the dispersive power of the crown glass.
Answer:
Given δ_V = 3.75°, δ_Y = 3.25°, δ_R = 2.86°
Using the expression for dispersive power \(\mathrm{D} \mathrm{P}=\frac{\delta_{\mathrm{V}}-\delta_{\mathrm{R}}}{\delta_{\mathrm{Y}}}=\frac{3.75-2.86}{3.25}=0.27\)

Question 9. [2]
(a) What is meant by mass defect ?
(h) What conclusion is drawn from Rutherford’s scattering experiment of α -particles ?
Answer:
(a) This is the difference in mass of the constituent nucleons and the nucleus formed.
(b) That the entire positive charge and 99 % mass is concentrated in the center of the atom called the nucleus.

Question 10. [2]
Define the following with reference to photoelectric effect:
(i) Threshold frequency (f₀)
(ii) Stopping potential (V_s)
Answer:
(i) It is the minimum frequency below which photoelectric effect does not take place.
(ii) It is the negative potential of the anode for which even the fasts moving electrons cannot reach it.

Question 11. [2]
(a) The half-life of radium is 1550 years. Calculate its disintegration constant (λ).
Or
(b) Copy and complete the following table for a radioactive element whose half-life is 10 minutes. Assume that you have 30 g of this element at t = 0.

Answer:

Question 12. [2]
Define frequency modulation and state any one advantage of frequency modulation (FM) over amplitude modulation (AM).
Answer:
When the frequency of the carrier wave changes in accordance with the frequency of the signal it is called frequency modulation. External noise does not have any effect on frequency modulation.

Section – C
Answer all questions.

Question 13. . [3]
Obtain an expression for electric potential ‘V’ at a point in an end-on position i.e., axial position of an electric dipole.
Answer:
Consider an electric dipole consisting of -q and +q charges separated by a distance 2a as shown in figure below. Let P be the point of observation where the electric potential has to be found. Let it be at a distance r from the center O of the dipole. Let us suppose that the dipole is placed in vacuum.

Question 14. [3]
Three capacitors of capacitance C₁ = 3 μf C₂ = 6 μf and C₃ = 10 μf are connected to a 10 V battery as shown in Figure 3 below :

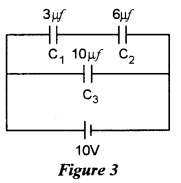
Calculate: .
(a) Equivalent capacitance.
(b) Electrostatic potential energy stored in the system.
Answer:

Question 15. [3]
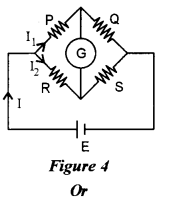
(a) Obtain the balancing condition for the Wheatstone bridge arrangement as shown in Figure 4 below:

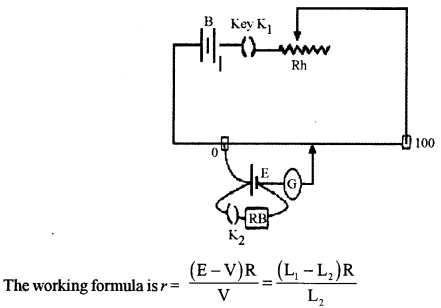
(b) Draw a labelled circuit diagram of a potentiometer to measure the internal resistance ‘r’ of a cell. Write the working formula (derivation is not required).
Answer:
(a) Consider the diagram as shown below. The distribution of current in accordance with Kirchhoff’s rules is shown.
Applying Kirchhoff’s loop rule to the closed loop ABDA, we have
\(-\mathrm{I}_{1} \mathrm{P}-\mathrm{I}_{\mathrm{g}} \mathrm{G}+\left(\mathrm{I}-\mathrm{I}_{1}\right) \mathrm{R}=0 \) …(1)


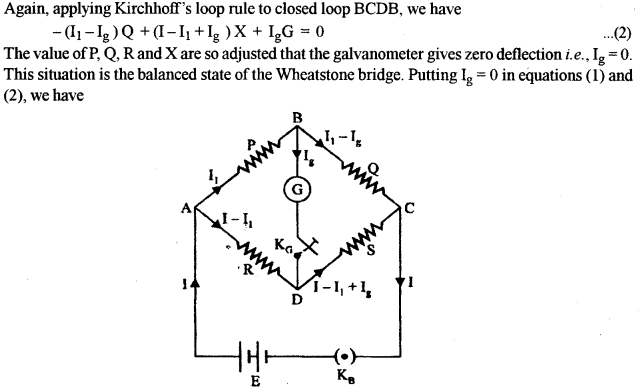
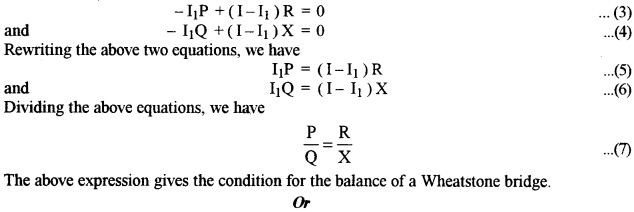
b) The circuit diagram is as shown:

Question 16. [3]
(a) A ray of light is incident on a prism whose refractive index is 1.52 at anagle of 40°. If the angle of emergence is 60°, calculate the angle of the prism.
Or
(b) Calculate the focal length of a convex lens whose radii of curvature of two surfaces is 10 cm and 15 cm respectively and its refractive index is 1.5.
Answer:

Question 17.  [3]
Derive the law of reflection using Huygens’s Wave Theory.
Answer:
Consider a plane wave front AB incident obliquely on a plane reflecting surface MM’. Let us consider the situation when one end A of wave front strikes the mirror at an angle i but the other end B has still to cover distance BC. Time required for this will be t = BC/ c.

According to Huygens’s principle, point A starts emitting secondary wavelets and in time t, these will cover a distance c,t = BC and spread. Hence, with point A as center and BC as radius, draw a circular arc. Draw tangent CD on this arc from the point C. Obviously. CD is the reflected wave front inclined at an angle r. As incident wave front and reflected wave front both are in the plane of paper, 1st law of reflection is proved.

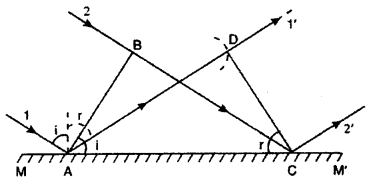
To prove second law of reflection, consider ΔABC and ΔADC. BC = AD (by construction)
∠ABC = ∠ADC = 90° and AC is common. Therefore, the two triangles are congruent and, hence, ∠B AC = ∠DCA or ∠i = ∠r i.e., the angle of reflection is equal to the angle of incidence, which is the second law of reflection.

Question 18. [3]
State any two Bohr’s postulates and write the energy value of the ground state of the hydrogen atom.
Answer:

• Only those orbits are allowed for which the angular momentum of the electron about the nucleus is an integral multiple of h/2h , where h is Planck’s constant.
• Energy is radiated when an electron “jumps” from one allowed stationary orbit to another.
  E = -13.6 eV

Question 19. [3]
With reference to semiconductors answer the following :
(i) What is the change in the resistance of the semiconductor with increase in temperature ?
(ii) Name the majority charge carriers in n-type semiconductor.
(iii) What is meant by doping ?
Answer:
(i) It decreases.
(ii) Electrons.
(iii) It is the addition of an impurity in a pure semiconductor.

Section – D
Answer all questions.

Question 20. [5]
(a) An alternating emf of 200 V, 50 Hz is applied to an L – R circuit, having a resistance R of 10 Ω . and an inductance L of 0.05 H connected in series. Calculate :
(1) Impedance.
(2) Current flowing in the circuit.

(ii) Draw a labelled graph showing the variation of inductive reactance (XL) verses frequency (f).
OR
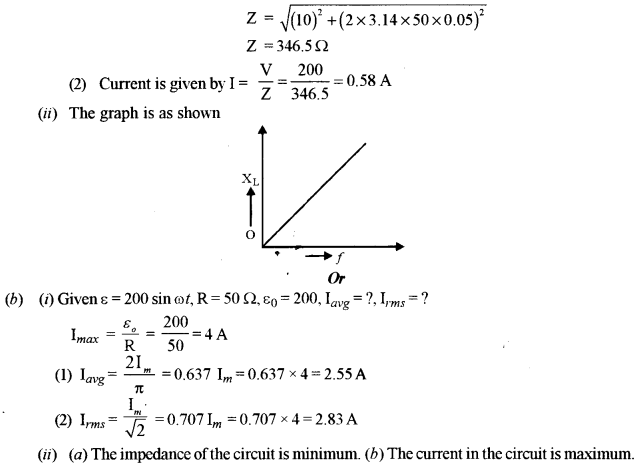
(i) An a.c. source of emf e = 200 sin ωt is connected to a resistor of 50 Ω
Calculate:
(1) Average current (I_avg).
(2) Root mean square (rms) value of emf.
(ii) State any two characteristics of resonance in an LCR series circuit.
Answer:


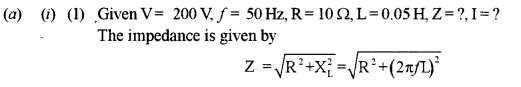
Question 21. [5]
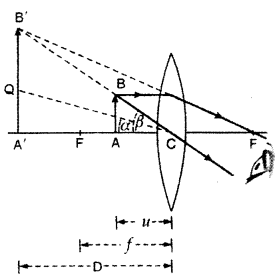
(a) Draw a neat labelled ray diagram showing the formation of an image at the least distance of distinct vision D by a simple microscope. When the final image is at D. derive an expression for its magnifying power at D.
(b) Draw a neat labelled diagram of Young’s Double Slit experiment. Show that β =λD/d , where the terms have their usual meaning (either for bright or dark fringe).
Answer:
(a) The diagram is as shown:


(b) Consider a point P on the viewing screen; the screen is located at a perpendicular distance D from the screen containing the slits S₁ and S₂, which are separated by a distance das shown in figure. Let us assume that the source of light is monochromatic having a wavelength λ. Under these conditions, the waves emerging from S₁ and S₂ have the same frequency and amplitude and are in phase.

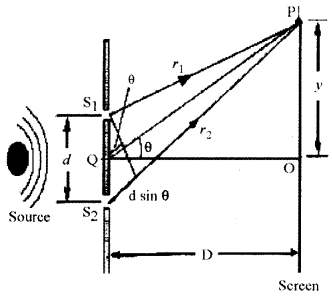
The light intensity on the screen at P is the resultant of the lights coming from both the slits. As seen in the diagram a wave from the lower slit travels farther than a wave from the upper slit. This difference in path is called the path difference. Therefore, if ‘x’ is the path difference between the waves from slits S₂ and S₁ at point P, then
\(x=r_{2}-r_{1}=d \sin \theta\) …..(1)

where it is assumed that r₁ and r₂ are parallel, which is approximately true because D is much greater than d. The value of this path difference determines whether or not the two waves are in phase, when they arrive at point P.

If the path difference is either zero or some integral multiple of the wavelength, the waves are in phase at P and constructive interference results. Therefore, the condition for bright fringes, or constructive interference, at P is given by
\(x=d \sin \theta=n \lambda\) …………(2)

In order to find the position of maxima measured vertically from O to P i.e., y we assume that D >> d. Under these conditions, θ is small, and so the approximation sin θ ~ tan θ. Therefore, from triangle POQ in figure, we find that




Question 22.
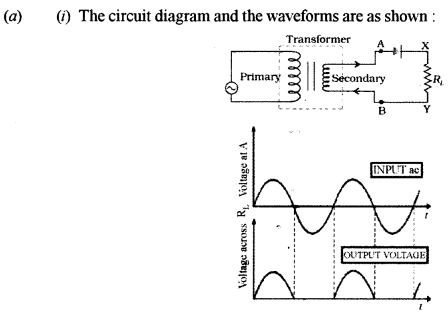
(a) (i) Draw a labelled circuit diagram of a half wave rectifier and give its output waveform.
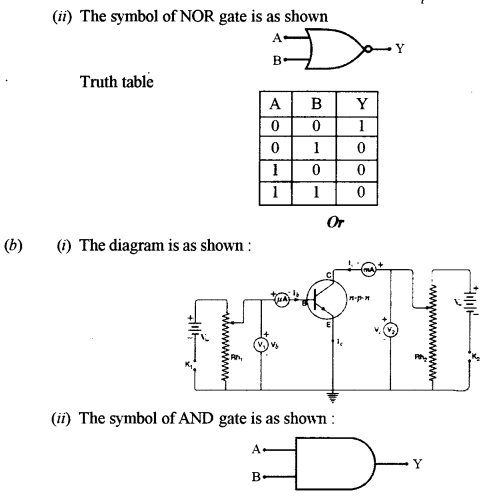
(ii) Draw a symbol of NOR gate and write its truth table.
Or
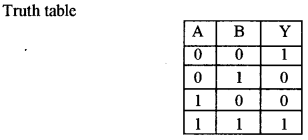
(b) (i) Draw a neat circuit diagram to study the input and output characteristics of a common emitter transistor.
(ii) Draw the symbol for AND gate and write its truth table.

Answer:

ISC Class 12 Physics Previous Year Question Papers