ISC Maths Question Paper 2019 Solved for Class 12

ISC Maths Previous Year Question Paper 2019 Solved for Class 12

Time Allowed: 3 Hours
Maximum Marks: 100

(Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.)

• The Question Paper consists of three sections A, B and C.
• Candidates are required to attempt all questions from Section A and all questions EITHER from Section B or Section C.
• Section A: Internal choice has been provided in three questions of four marks each and two questions of six marks each.
• Section B: Internal choice has been provided in two questions of four marks each.
• Section C: Internal choice has been provided in two questions of four marks each.
• All working, including rough work, should be done on the same sheet as, and adjacent to the rest of the answer.
• The intended marks for questions or parts of questions are given in brackets [ ].
• Mathematical tables and graph papers are provided.

Section – A (80 Marks)

Question 1. [10 × 2]
(i) If f: R → R, f(x) = x³ and g: R → R, g (x) = 2x² + 1, and R is the set of real numbers, then find fog(x) and gof(x).
(ii) Solve: sin (2 tan^-1x) = 1.
(iii) Using determinants, find the values of k, if the area of triangle with vertices (-2, 0), (0, 4) and (0, k) is 4 square units.
(iv) Show that (A + A’) is symmetric matnx. if A = \(\begin{pmatrix} 2 & 4 \\ 3 & 5 \end{pmatrix}\)
(v) f(x) = \(\frac { { x }^{ 2 }-9 }{ x-3 }\) is not defined at x = 3. What value should be assigned to f(3) for continuity of f(x) at x = 3?
(vi) Prove that the function f(x) = x³ – 6x² + 12x + 5 is increasing on R.
(vii) Evaluate:

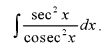
(viii) UsingL Hospital’s Rule, evaluate:

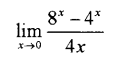
(ix) Two balls are drawn from an urn containing 3 white, 5 red and 2 black balls, one by one without replacement. What is the probability that at least one ball is red?
(x) If events A and B are independent, such that P( A) = \(\frac { 3 }{ 5 }\), P (B) = \(\frac { 2 }{ 3 }\), find P(A∪B).
Solution:

Question 2.
If f: A → A and A = R – {\(\frac { 8 }{ 5 }\)}, show that the function f(x) = \(\frac { 8x+3 }{ 5x-8 }\) is one-one onto. Hence, find f^-1.
Solution:
Given function is:

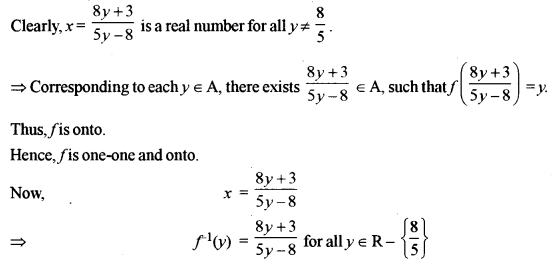
Question 3.
(a) Solve for x:

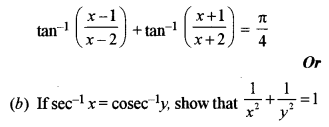
Solution:

Question 4.
Use properties of determinants prove that:

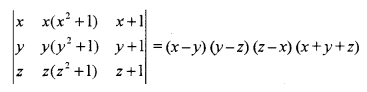
Solution:

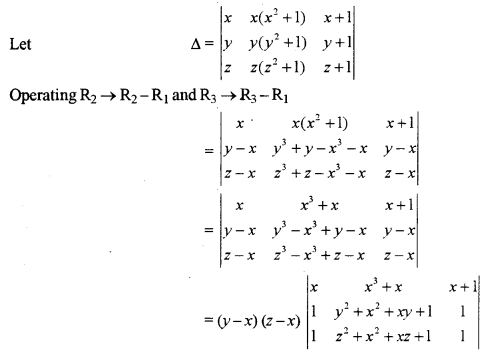
Question 5. [4]
(a) Show that the function f(x) = |x – 4|, x ∈ R is continuous, but not differentiable at x = 4.
Or
(b) Verify the Lagrange’s mean value theorem for the function:
f(x) = x + \(\frac { 1 }{ x }\) in the interval [1, 3]
Solution:

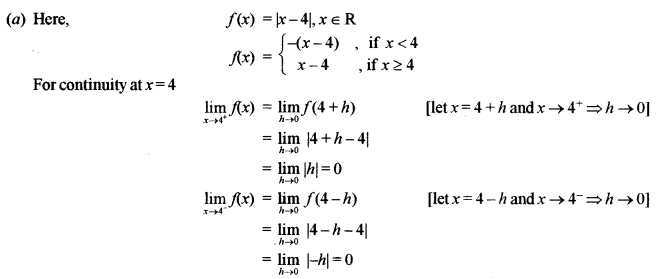
Thus, f(x) is continuous at x = 4.
For differentiability at x = 4.
When x < 4, f(x) = -(x – 4), which being polynomial function is differentiable for all x < 4.
When x > 4, f(x) = x – 4, which being polynomial function is differentiable for all x > 4.
When x = 4

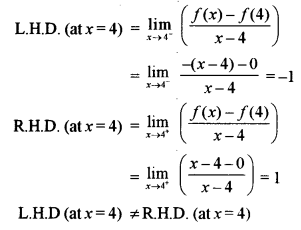
Hence, f(x) is not differentiable at x = 4.
Or
(b) Let f(x) = x + \(\frac { 1 }{ x }\) in the inverval [1, 3]
Since, f(x) is a polynomial function, therefore, it is continuous and derivable in (1, 3).
⇒ f satisfies conditions of Mean Value theorem in [1, 3],
Thus, there exists atleast one real c ∈ (1, 3) such that


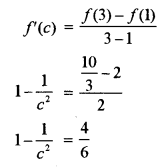
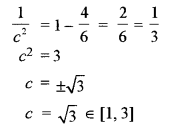
Hence, Mean Value theorem for the given function is verified in the given interval.

Question 6.

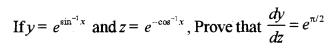
Solution:

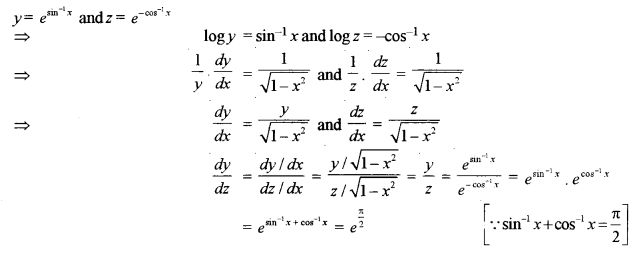
Question 7.
A 13 m long ladder is leaning against a wall, touching the wall at a certain height from the ground level. The bottom of the ladder is pulled away from the wall, along the ground, at the rate of 2 m/s. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall?
Solution:
Let at any instant of time t, the height of the top of the ladder be y and its foot be at distance x from the wall, then

Question 8.

Solution:

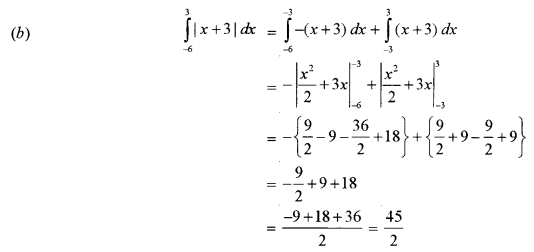
Question 9.
Solve the differential equation:

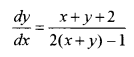
Solution:
Given the differential equation is

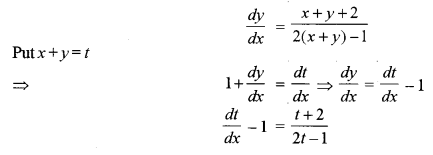
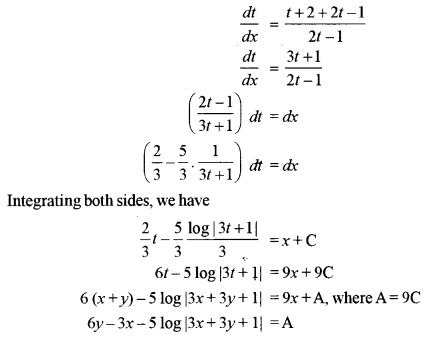
Question 10. [4]
Bag A contains 4 white balls and 3 black balls, while Bag B contains 3 white balls and 5 black balls. Two balls are drawn from Bag A and placed in Bag B. Then, what is the probability of drawing a white ball from Bag B?
Solution:
Here, we have three cases
Case 1: Two balls drawn from Bag A are White.
Case 2: Two balls drawn from Bag A are Black.
Case 3: Two balls drawn from Bag A are one White and other Black.

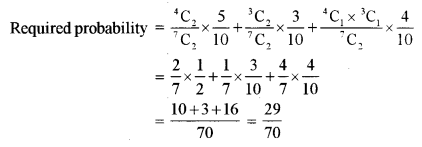
Question 11. [6]
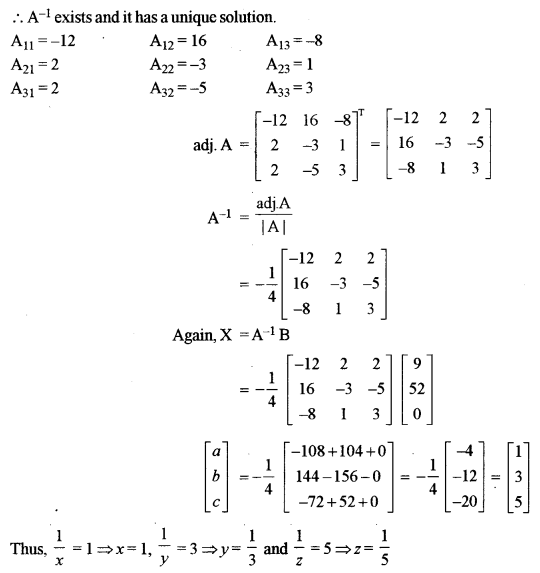
Solve the following system of linear equations using matrix method:

Solution:

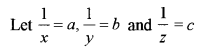
Question 12. [6]
(a) The volume of a closed rectangular metal box with a square base is 4096 cm³. The cost of polishing the outer surface of the box is ₹ 4 per cm². Find the dimensions of the box for the minimum cost of polishing it.
Or
(b) Find the point on the straight line 2x + 3y = 6, which is closest to the origin.
Solution:

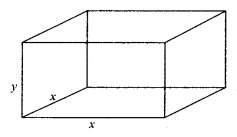
(a) Let x be the side of the square base andy be its height.

Question 13. [6]

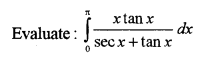
Solution:

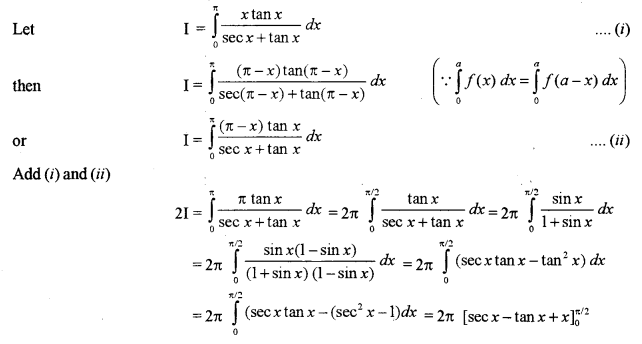
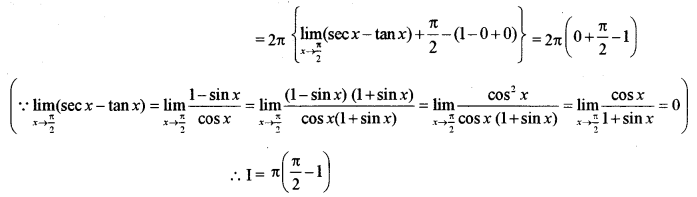
Question 14.
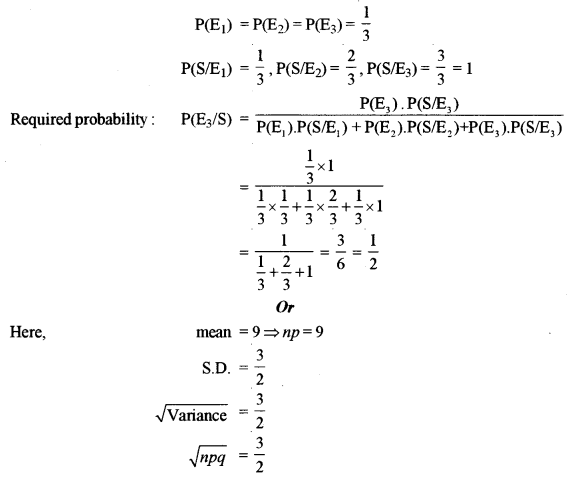
(a) Given three identical Boxes A, B and C, Box A contains 2 gold and 1 silver coin, Box B contains 1 gold and 2 silver coins and Box C contains 3 silver coins. A person chooses a Box at random and takes out a coin. If the coin drawn is of silver, find the probability that it has been drawn from the Box which has the remaining two coins also of silver.
Or
(b) Determine the binomial distribution where mean is 9 and standard deviation is \(\frac { 3 }{ 2 }\). Also, find the probability of obtaining at most one success.
Solution:
(a) Let E₁, E₂, E₃ be the three events of the selection of three bags A, B and C respectively.
Let S be the event that the coin drawn is of silver, we have

Section – B (20 Marks)

Question 15. [3 × 2]
(a) If \(\vec { a }\) and \(\vec { b }\) are perpendicular vectors, \(\left| \vec { a } +\vec { b } \right| =13\) 13 and \(\left| \vec { a } \right|\) = 5. find the value of \(\left| \vec { b } \right|\).
(b) Find the length of the perpendicular from origin to the plane \(\vec { r } \cdot \left( 3\hat { i } -4\hat { j } -12\hat { k } \right) +39=0\)
(c) Find the angle between the two lines 2x = 3y = -z and 6x = -y = -4z.
Solution:
(a) Here, \(\vec { a }\) and \(\vec { b }\) are perpendicular vectors

(b) Length of the perpendicular from the origin O(0, 0, 0) to the given plane

(c) Given lines are:

Hence, the lines are perpendicular to each other.

Question 16.

Solution:

Question 17. [4]
(a) Find the equation of the plane passing through the intersection of the planes 2x + 2y – 3z – 7 = 0 and 2x + 5y + 3z – 9 = 0 such that the intercepts made by the resulting plane on the x – axis and the z – axis are equal.
Or
(b) Find the equation of the lines passing through the point (2, 1, 3) and perpendicular to the lines

Solution:
(a) Given planes are:
2x + 2y – 3z – 7 = 0 … (i)
and 2x + 5y + 3z – 9 = 0 … (ii)
Equation of the plane passing through the intersection of the planes (i) and (ii) is:

Question 18. [6]
Draw a rough sketch and find the area bounded by the curve x² = y and x + y = 2.
Solution:

The given curves are: x² = y
Which is an upward parabola with vertex at origin
And line x + y = 2 ⇒ y = 2 – x
x² = 2 – x
⇒ x² + x – 2 = 0
⇒ (x + 2)(x – 1) = 0
⇒ x = -2 and x = 1
Now, y = 2-(-2) = 4
and y = 2 – 1 ⇒ y = 1
⇒ y = 4 and y = 1
Thus, the points of intersection are (-2, 4) and (1, 1)
Required area of shaded region

Section – C (20 Marks)

Question 19.
(a) A company produces a commodity with ₹ 24,000 as fixed cost. The variable cost estimated to be 25% of the total revenue received on selling the product, is at the rate of ₹ 8 per unit. Find the break-even point.
(b) The total cost function for a production is given by C (x) = \(\frac { 3 }{ 4 }\) x² – 7x + 27.
Find the number of units produced for which M.C. = AC.
(M.C. = Marginal Cost and A.C. = Average Cost)
(c) If \(\vec { x }\) = 18, \(\vec { x }\) = 100, σ_x = 14, σ_y = 20 and correlation coefficient r_xy = 0.8, find the reggression equation of y on x.
Solution:
(a) Suppose that x number of the unit be produced and sold.
As each unit’s variable cost is 25% of revenue
The variable cost of x units = 25 % of ₹ 8x = ₹ 2x
Total cost of producing x units C(x) = TFC + TVC = ₹ (24000 + 2x)
Price of one unit = ₹ 8
Total revenue of selling x units = R(x) = ₹ 8x
At break-even values,
C(x) = R(x)
⇒ 24000 + 2x = 8x
⇒ 24000 = 6x
⇒ x = 4000
(b) Total cost function for a production

Question 20. [4]
(a) The following results were obtained with respect to two variables x and y:
Σx = 15, Σy = 25, Σxy = 83, Σx² = 55, Σy2 = 135 and n = 5
(i) Find the regression coefficient bxy.
(ii) Find the regression equation of x on y.
Or
(b) Find the equation of the regression line of y on x, if the observations (x, y) are as follows:
(1, 4), (2, 8), (3, 2), (4, 12), (5, 10), (6, 14), (7, 16), (8, 6), (9, 18)
Also, find the estimated value of y when x = 14.
Solution:

Question 21. [4]
(a) The cost function of a product is given by C (x) = \(\frac { { x }^{ 3 } }{ 3 }\) – 45x² – 900x + 36, where x is the number of units produced. How many units should be produced to minimise the marginal cost?
Or
(b) The marginal cost function of x units of a product is given by MC = 3x² – 10x + 3. The cost of producing one unit is ₹ 7. Find the total cost function and average cost function.
Solution:

Question 22. [6]
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to produce product A and product B. Each unit of product A requires 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for ₹ 48 per unit and product B is sold for ₹ 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income?
Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
Solution:
Let x units of product A and y units of product B be produced and sold by the carpenter. Then information given in the statement is tabulated as:

Then the LPP is maximise P = 48x + 40y
Subject to the constraints:
2x + y ≤ 90 …..(i)
x + 2y ≤ 80 ….. (ii)
x + y ≤ 50 ….. (iii)
x ≥ 0, y ≥ 0

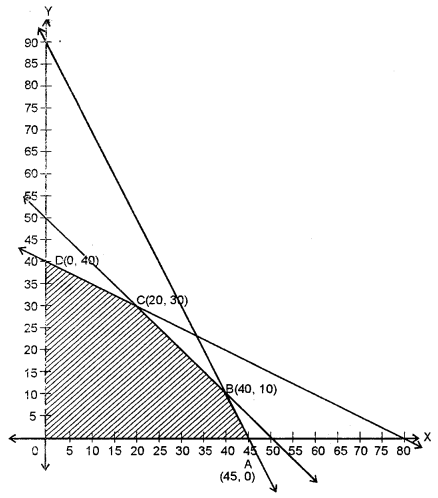
Draw the graphs of equations (i), (ii), (iii)
Then shaded region is the required feasible region which is bounded with comer points
O(0, 0), A(45, 0), B(40, 0), C(20, 30) and D(0, 40).
At O(0, 0), the value of P = 0 + 0 = 0
At A(45, 0), the value of P = 48 × 45 + 0 = 2160
At B(40,10), the value of P = 48 × 40 + 40 × 10 = 2320 → Maximum
At C(20, 30), the value of P = 48 × 20 + 40 × 30 = 2160
At D(0, 40), the value of P = 0 + 40 × 40 = 1600
We have the maximum value of P as ₹ 2320 and it is obtained at the vertex B (40, 10).
Hence, the maximum gross income of the carpenter should make 40 units of product A and 10 units of product B.

ISC Class 12 Maths Previous Year Question Papers