ISC Maths Question Paper 2015 Solved for Class 12

ISC Maths Previous Year Question Paper 2015 Solved for Class 12

Time Allowed: 3 Hours
Maximum Marks: 100

(Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.)

The Question Paper consists of three sections A, B and C.
Candidates are required to attempt all questions from Section A and all questions either from Section B or Section C.
Section A: Internal choice has been provided in three questions of four marks each and two questions of six marks each.
Section B: Internal choice has been provided in two questions of four marks each.
Section C: Internal choice has been provided in two questions of four marks each.
All working, including rough work, should be done on the same sheet as, and adjacent to the rest of the answer.
The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables and graph papers are provided.

Section – A

Question 1. [10 × 3]
(i) Find the value of k if M = $M=\left[\begin{array}{ll}{1} & {2} \\ {2} & {3}\end{array}\right]$ and M² – kM – I₂ = 0
(ii) Find the equation of an ellipse whose latus rectum is 8 and eccentricity is $\frac { 1 }{ 3 }$ .
(iii) Solve: $\cos ^{-1}\left(\sin \cos ^{-1} x\right)=\frac{\pi}{6}$
(iv) Using L’ Hospital’s rule, evaluate: $\lim _{x \rightarrow 0} \frac{x-\sin x}{x^{2} \sin x}$
(v) Evaluate: $\int \frac{2 y^{2}}{y^{2}+4} d y$
(vi) Evaluate: $\int_{0}^{3} f(x) d x, \text { where } f(x)=\left\{\begin{array}{ll}{\cos 2 x, 0 \leq x} & { \leq \frac{\pi}{2}} \\ {3,} & {\frac{\pi}{2} \leq x \leq 3}\end{array}\right\}$
(vii) The two lines of regressions are 4x + 2y – 3 = 0 and 3x + 6y + 5 = 0. Find the correlation co-efficient between x and y.
(viii) A card is drawn from a well shuffled pack of playing cards. What is the probability that it is either a spade or an ace or both?
(ix) If 1, ω and ω² are the cube roots of unity, prove that $\frac{a+b \omega+c \omega^{2}}{c+a \omega+b \omega^{2}}=\omega^{2}$
(x) Solve the differential equation: $\sin ^{-1}\left(\frac{d y}{d x}\right)=x+y$
Solution:

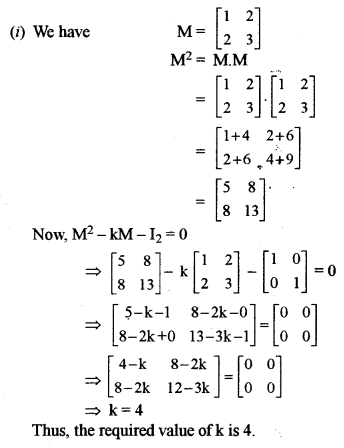
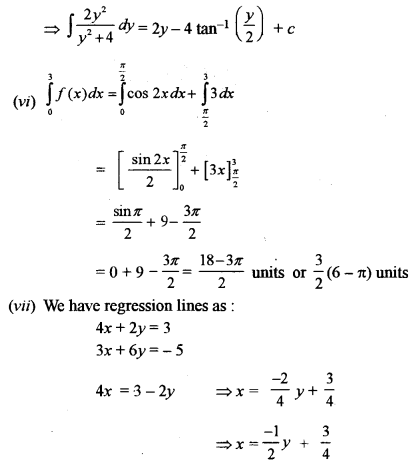
Question 2.
(a) Using properties of determinants, prove that: [5]

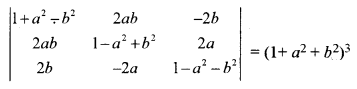
(b) Given two matrices A and B [5]

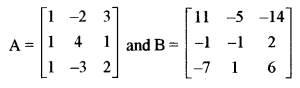
find AB and use this result to solve the following system of equations:
x – 2y + 3 = 6, x + 4y + z = 12, x – 3y + 2z = 1
Solution:

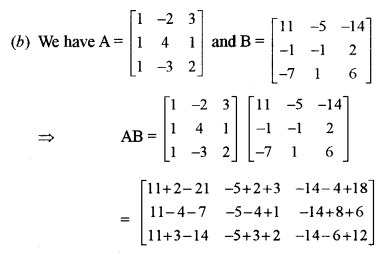
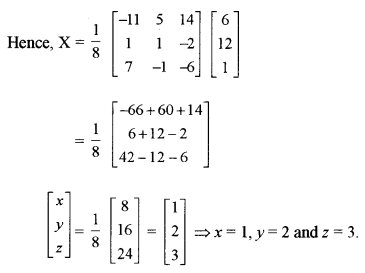
Question 3.
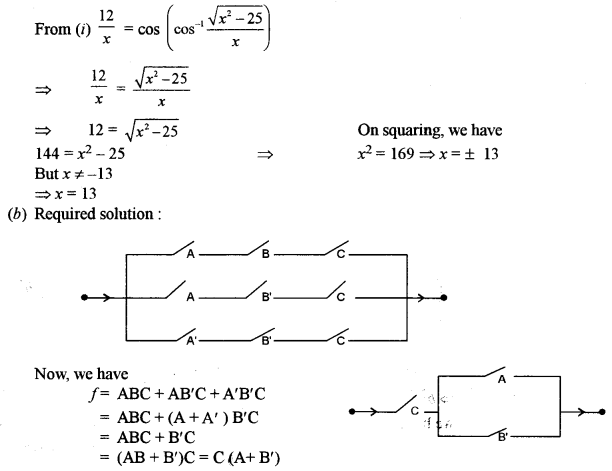
(a) Solve the equation for x: $\sin ^{-1} \frac{5}{x}+\sin ^{-1} \frac{12}{x}=\frac{\pi}{2}, x \neq 0$ [5]
(b) A, B and C represent switches in ‘on’ position and A’, B’ and C’ represent them in ‘off’ position. Construct a switching circuit representing the polynomial ABC + A B’ C + A’ B’ C. Using Boolean Algebra, prove that the given polynomial can be simplified to C (A+ B’). Construct an equivalent switching circuit. [5]
Solution:

Question 4.
(a) Verily Lagrange’s Mean Value Theorem for the following function: [5]
f(x) = 2 sin x + sin 2x on [0, π]
(b) Find the equation of the hyperbola whose foci are (0, ± √10 ) and passing through the point (2, 3). [5]
Solution:
(a) The function f(x) = 2 sin x + sin 2x is derivable for all values of x, hence derivable in (0, π) also
Now, f'(x) = 2 cos x + 2 cos 2x
Using Lagrange’s Mean Value Theorem;

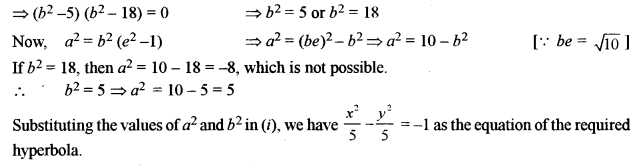
Question 5.

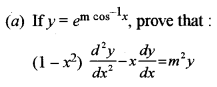
(b) Show that the rectangle of the maximum perimeter which can be inscribed in a circle of radius 10 cm is a square of side 10√2 cm.
Solution:

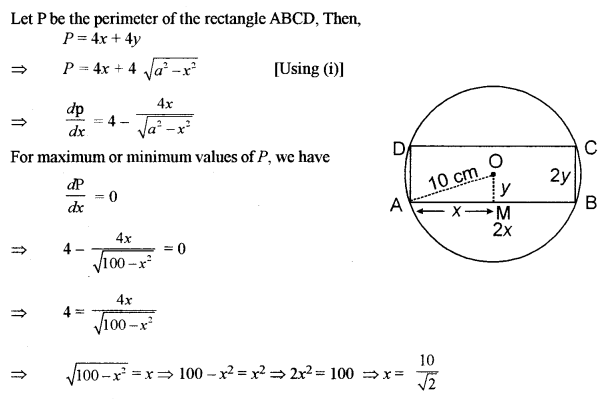
Question 6.
(a) Evaluate: [5]
$\int \frac{\sec x}{1+\csc x} d x$
(b) Find the smaller area enclosed by the circle x² + y² = 4 and the line x + y = 2.
Solution:

Question 7.
(a) Given that the observations are: [5]
(9, -4), (10, -3), (11, -1), (12, 0), (13, 1), (14, 3), (15, 5), (16, 8).
Find the two lines of regression and estimate the value of y when x = 13.5
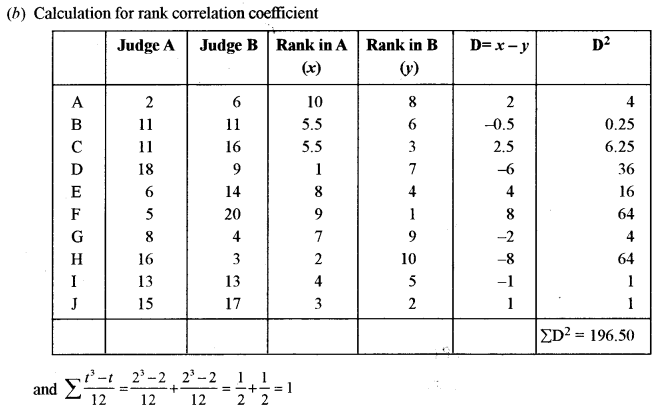
(b) In a contest, the competitors are awarded marks out of 20 by two judges. The scores of the 10 competitors are given below. Calculate Spearman’s rank correlation. [5]

Solution:
(a) We have the following calculation for regression equations

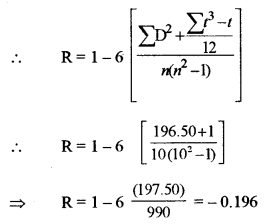
Question 8.
(a) An um contains 2 white and 2 black balls. A ball is drawn at random. If it is white, it is not replaced into the um. Otherwise, it is replaced with another ball of the same colour. The process is repeated. Find the probability that the third ball is drawn is black. [5]
(b) Three persons A, B and C shoot to hit a target. If A hits the target four times in five trials, B hits it three times in four trials and C hits it two times in three trials, find the probability that: [5]
(i) Exactly two persons hit the target.
(ii) At least two persons hit the target.
(iii) None hit the target.
Solution:
(a) Using a tree diagram:
Since there are 2 white and 2 black balls.

Question 9.
(a) If $z=x+i y, w=\frac{2-i z}{2 z-i} \quad \text { and }|w|=1$ find the locus of z and illustrate it in the Aigand Plane. [5]
(b) Solve the differential equation:
$\mathrm{e}^{\frac{x}{y}}\left(1-\frac{x}{y}\right)+\left(1+\mathrm{e}^{\frac{x}{y}}\right) \frac{d x}{d y}=0 \text { when } x=0, y=1$ [5]
Solution:

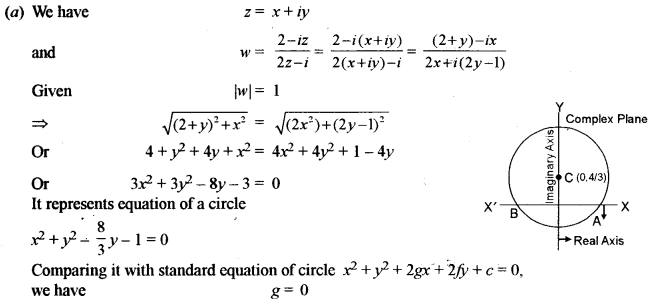
Section – B

Question 10.
(a) Using vectors, prove that angle in a semicircle is a right angle. [5]
(b) Find the volume of a parallelopiped whose edges are represented by the vectors: [5]
$\vec{a}=2 \hat{i}-3 \hat{j}-4 \hat{k}, \vec{b}=\hat{i}+2 \hat{j}-\vec{k}, \text { and } \vec{c}=3 \hat{i}+\hat{j}+2 \hat{k}$
Solution:

Question 11.
(a) Find the equation of the plane passing through the intersection of the planes: [5]
x + y + z + 1 = 0 and 2x – 3y + 5z – 2 = 0 and the point (-1, 2, 1).
(b) Find the shortest distance between the lines $\vec{r}=\hat{i}+2 \hat{j}+3 \hat{k}+\lambda(2 \hat{i}+3 \hat{j}+4 \vec{k})$ and
$\vec{r}=2 \hat{i}+4 \hat{j}+5 \hat{k}+\mu(4 \hat{i}+6 \hat{j}+8 \vec{k})$ [5]
Solution:
(a) The equation of any plane passing through the line of intersection of the given plane.
x + y + z + 1 = 0 and 2x – 3y + 5z – 2 = 0 can be written as
x + y + z + 1 – k (2x – 3y + 5z – 2) = 0 ……. (i)
Where k is any real number
Now, if the plane passes through the point (-1, 2, 1)

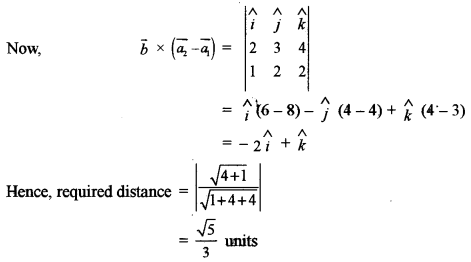
Question 12.
(a) Box I contains two white and three black balls. Box II contains four white and one black balls and box III contains three white and four black balls. A dice having three red, two yellow and one green face, is thrown to select the box. If red face turns up, we pick up the box I, if a yellow face turns up we pick up box II, otherwise, we pick up box III. Then we draw a ball from the selected box. If the ball drawn is white, what is the probability that the dice had turned up with a red face? [5]
(b) Five dice are thrown simultaneously if the occurrence of an odd number in a single dice is considered a success, find the probability of maximum three successes. [5]
Solution:
(a) Considered the following events:
E₁, E₂, E₃ be pertaining to the red-faced dice yellow face and green-faced die
P(E₁) = $\frac { 3 }{ 6 }$ = $\frac { 1 }{ 2 }$
Probability of getting white ball from Box I = $\frac { 2 }{ 5 }$
Probability of getting a white ball from box II = $\frac { 4 }{ 5 }$
Probability of getting a white ball from box II = $\frac { 3 }{ 7 }$
Using Baye’s theorem
Required probability

Section – C

Question 13.
(a) Mr Nirav borrowed ₹ 50,000 from the bank for 5 years. The rate of interest is 9% per annum compounded monthly. Find the payment he makes monthly if he pays back at the beginning of each month. [5]
(b) A dietician wishes to mix two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12units of vitamin Band 8 units of vitamin C. The vitamin contents of one kg food is given below:

One kg of food X costs ₹ 24 and one kg of food Y costs ₹ 36. Using Linear Programming, find the least cost of the total mixture which will contain the required vitamins. [5]
Solution:
(a) Nirav borrowed amount V = ₹ 50000
Interest (i) = 9% per annum = $\frac { 9 }{ 12 }$ per month
Number of months = 60
Now,

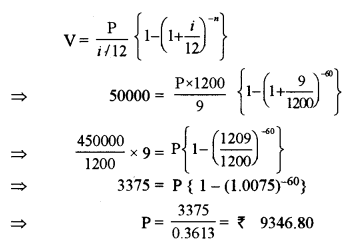
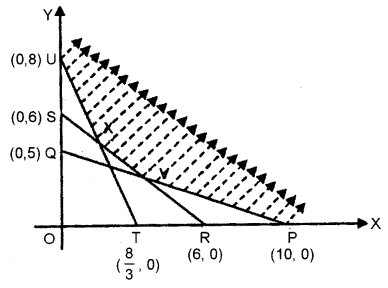
(b) Let x kg of food X and y kg of food Y be mixed in the desired diet.
Therefore, the linear programming problem is to minimize Z = 24x + 36y subject to the constraints:
x + 2y ≥ 10
2x + 2y ≥ 12
3x + y ≥ 8
are drawn with x = 0 as the y – axis and y = 0 as the x-axis.
Thus, the lines PQ : x + 2y = 10, RS: x + y = 6 and TU : 3x + y = 8
Now, PQ and RS meet at V (2, 4), RS and TU meet at X (1, 5).
The shaded region in the graph on the right side is the feasible region.
The value of Z = 24x + 36y at PVXU respectively
(i) At P (10, 0), Z_p = 24 × 10 + 136 × 0 = 240
(ii) At V (2, 4), Z_v = 24 × 2 + 36 × 4 = 192
(iii) At X (1, 5), Z_x = 24 × 1 + 36 × 5 = 204
(iv) At U(0, 8), Z_u = 24 × 0 + 36 × 8 = 288
From these values Z_v is the minimum value.
2 kg of food X and 4 kg of food Y are needed for required diet.

Question 14.
(a) A bill for ₹ 7650 was drawn on 8th March 2013, at 7 months. It was discounted on 18th May 2013 and the holder of the bill received ₹ 7497. What is the rate of interest charged by the bank? [5]
(b) The average cost function, AC for a commodity is given by AC = x + 5 + $\frac { 36 }{ x }$ , in terms of output x. Find:
(i) The total cost, C and marginal cost, MC as a function of x.
(ii) The outputs for which AC increases. [5]
Solution:

Question 15.
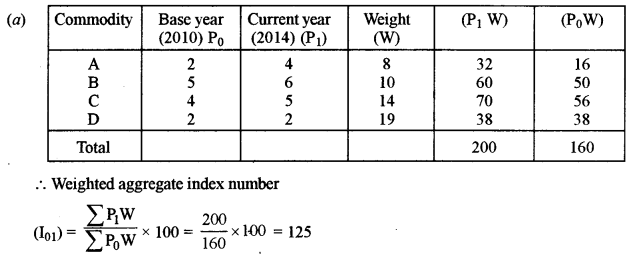
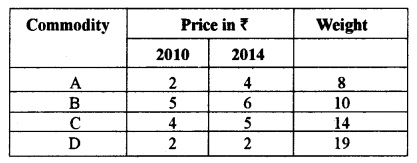
(a) Calculate the index number for the year 2014, with 2010 as the base year by the weighted aggregate method from the following data: [5]

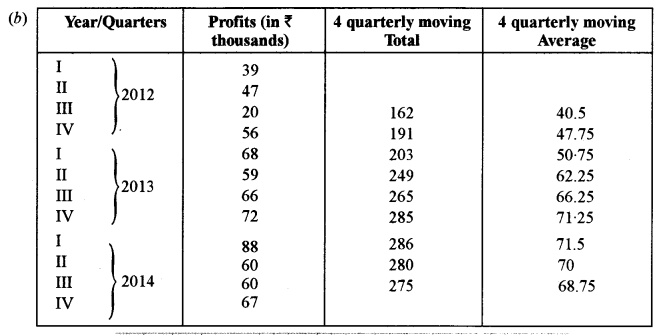
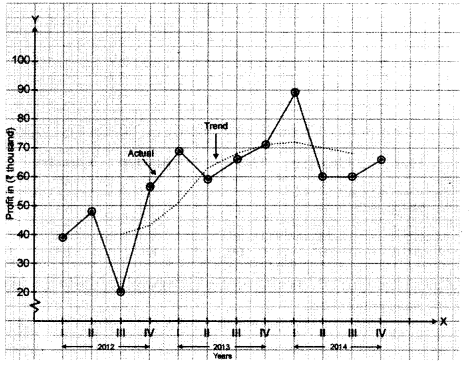
(b) The quarterly profits of a small scale industry (in thousands of rupees) is as follows:

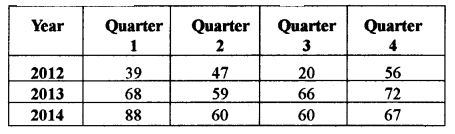
Calculate four quarterly moving averages. Display these and the original figures graphically on the same graph sheet.
Solution: