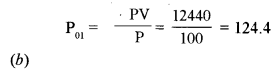ISC Maths Question Paper 2012 Solved for Class 12

ISC Maths Previous Year Question Paper 2012 Solved for Class 12

Time Allowed: 3 Hours
Maximum Marks: 100

(Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.)

• • The Question Paper consists of three sections A, B and C.
  • Candidates are required to attempt all questions from Section A and all questions either from Section B or Section C.
  • Section A: Internal choice has been provided in three questions of four marks each and two questions of six marks each.

• Section B: Internal choice has been provided in two questions of four marks each.
• Section C: Internal choice has been provided in two questions of four marks each.
• All working, including rough work, should be done on the same sheet as, and adjacent to the rest of the answer.
• The intended marks for questions or parts of questions are given in brackets [ ].
• Mathematical tables and graph papers are provided.

Section – A
(All questions are compulsory in this part)

Question 1.
(i) Solve for x if \(\left(\begin{array}{c}{x^{2}} \\ {y^{2}}\end{array}\right)+2\left(\begin{array}{l}{2 x} \\ {3 y}\end{array}\right)=3\left(\frac{7}{-3}\right)\) [3]
(ii) Prove that \(\sec ^{2}\left(\tan ^{-1} 2\right)+\csc ^{2}\left(\cot ^{-1} 3\right)=15\) [3]
(iii) Find the equation of the hyperbola whose Transverse and Conjugate axes are the x and y axes respectively, given that the length of conjugate axis is 5 and distance between the foci is 13. [3]
(iv) From the equations of the two regression lines, 4x + 3y + 7 = 0 and 3x + 4y + 8 = 0, find: [3]
(a) Mean of x and y.
(b) Regression coefficients.
(c) Coefficient of correlation.
(v) Evalulate: \(\int e^{x}(\tan x+\log \sec x) d x\) [3]
(vi) Evaluate: [3]

(vii) Find the locus of the complex number, Z = x + iy given \(\left|\frac{x+i y-2 i}{x+i y+2 i}\right|=\sqrt{2}\) [3]
(viii) Evaluate: \(\int_{1}^{2} \frac{\sqrt{x}}{\sqrt{3-x}+\sqrt{x}} d x\) [3]
(ix) Three persons A, B and C shoot to hit a target. If in trials, A hits the target 4 times in 5 shots, B hits 3 times in 4 shots and C hits 2 times in 3 trials. Find the probability that: [3]
(a) Exactly two persons hit the target.
(b) At least two persons hit the target.
(x) Solve the differential equation: [3]
(xy² + x)dx + (x²y + y) dy = 0
Solution:

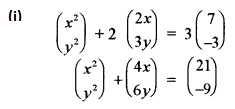
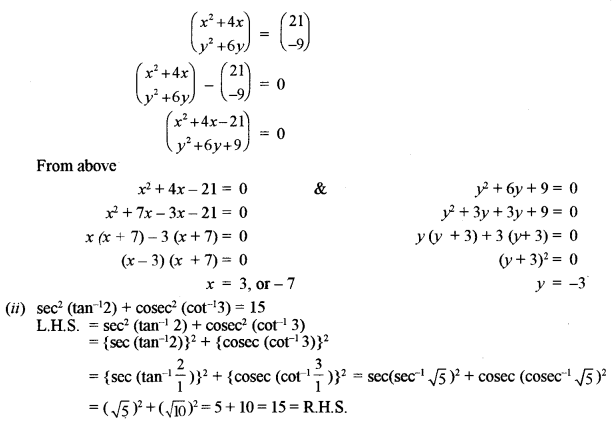
Question 2.
(a) Using properties of determinants, prove that: [5]
\(\left|\begin{array}{ccc}{a} & {a+b} & {a+b+c} \\ {2 a} & {3 a+2 b} & {4 a+3 b+2 c} \\ {3 a} & {6 a+3 b} & {10 a+6 b+3 c}\end{array}\right|=a^{3}\)
(b) Find the product of the matrices A and B where: [5]
\(A=\left(\begin{array}{ccc}{-5} & {1} & {3} \\ {7} & {1} & {-5} \\ {1} & {-1} & {1}\end{array}\right), B=\left(\begin{array}{lll}{1} & {1} & {2} \\ {3} & {2} & {1} \\ {2} & {1} & {3}\end{array}\right)\)
Hence, solve the following equations by matrix method:
x + y + 2z = 1
3x + 2y + z = 7
2x + y + 3z = 2
Solution:

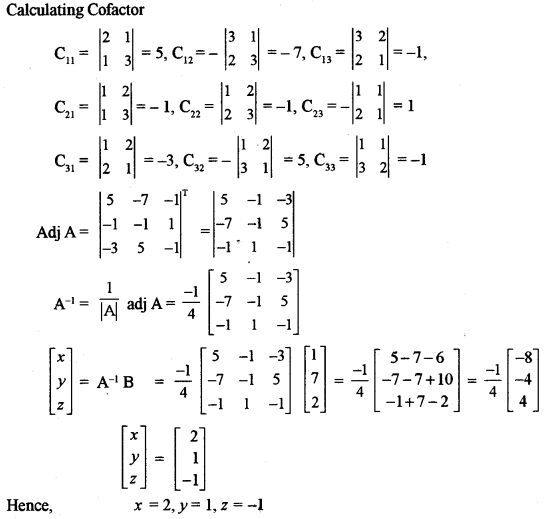
Question 3.
(a) Prove that: \(\cos ^{-1} \frac{63}{65}+2 \tan ^{-1} \frac{1}{5}=\sin ^{-1} \frac{3}{5}\) [5]
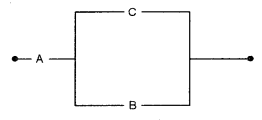
(b) (i) Write the Boolean expression corresponding to the circuit given below: [5]

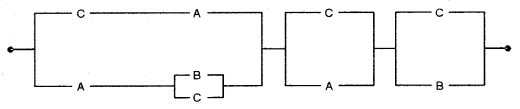
(ii) Simplify the expression using laws of Boolean Algebra and construct the simplified circuit.
Solution:

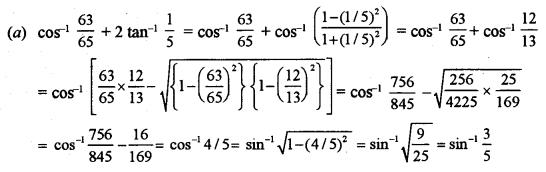
(b) (i) The statement using the given switching circuits is as:
CA + A(B + C) (C + A) (C + B) ….. (i)
using laws of Boolean Algebra, we have
CA + A(B + C) (C + A) (C + B) = (CA + AB + AC) (C + A) (C + B)
= (AC + AB + AC) (C + A) (C + B)
= ACC + ACA + ABC + ABA (C + B)
= AC + AC + ABC + AB (C + B)
= AC + ABC + ABC + AB
= AC + ABC + AB
= AC + AB (1 + C)
= AC + AB (1)
= AC + AB
= A(C + B)
Hence, the simplified switching network can be shown as in the figure.

Question 4.
(a) Verify Rolle’s theorem for the function: [5]
\(f(x)=\log \left\{\frac{x^{2}+a b}{(a+b) x}\right\}\) in the interval [a, b] where, 0 ∉ [a, b].
(b) Find the equation of the ellipse with its centre at (4, -1) focus at (1, -1) and given that it passes through (8, 0). [5]
Solution:
(a) Given
\(f(x)=\log \left(\frac{x^{2}+a b}{x(a+b)}\right) \log \left(x^{2}+a b\right)-\log x-\log (a+b)\)
Algorithmic function is differentiable and so continuous on .its domain. Therefore f(x) is continuous on [a, b] and differentiable on (a, b)
f(a) = f(b)

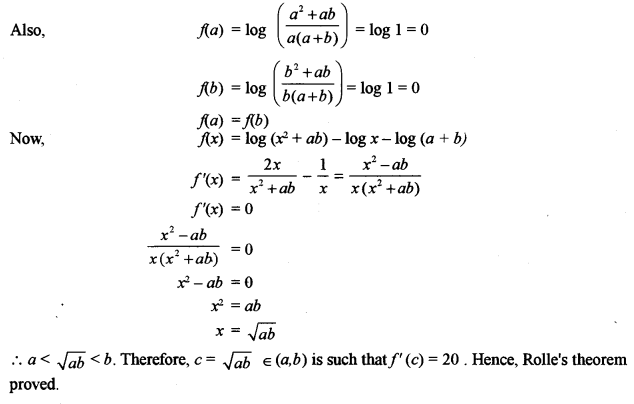
(b) Coordinate of the centre and focus are the same.
Therefore both lie on y = -1 & hence the major axis of the ellipse is parallel to the x-axis. & minor axis is parallel to the y-axis.
Let 2a & 2b be the length of major & minor axes respectively. Then the equation of the ellipse is

Question 5.
(a) If e^y (x + 1) = 1, then show that: [5]
\(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\)
(b) A printed page is to have a total area of 80 sq. cm with a margin of 1 cm at the top and on each side and a margin of 1.5 cm at the bottom. What should be the dimensions of the page so that the printed area will be maximum? [5]
Solution:

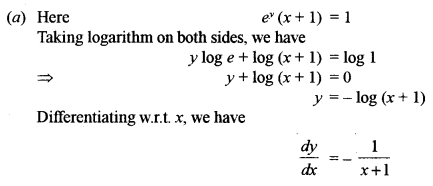
Question 6.
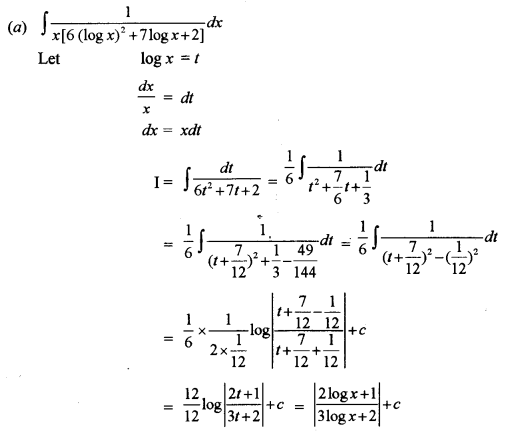
(a) Evaluate \(\int \frac{d x}{x\left\{6(\log x)^{2}+7 \log x+2\right\}}\) [5]
(b) Find the area of the region bounded by the curve x = 4y – y² and the y-axis. [5]
Solution:

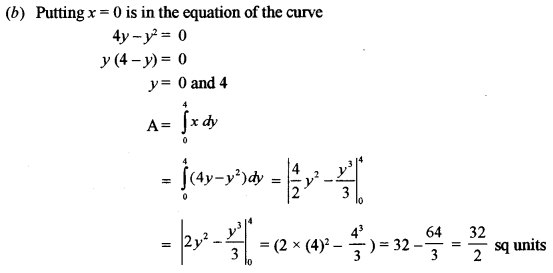
Question 7.
(a) Ten candidates received percentage marks in two subjects as follows: [5]

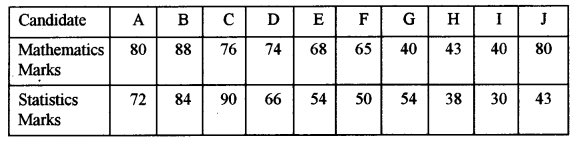
Calculate Spearman’s rank correlation coefficient and interpret your result.
(b) The following results were obtained with respect to two variables x and y: [5]
Σx = 30, Σy = 42, Σxy = 199, Σx² = 184, Σy² = 318, Σn = 6
Find the following:
(i) The regression coefficients.
(ii) Correlation coefficient between x and y.
(iii) Regression equation ofy on x.
(iv) The likely value ofy when x = 10.
Solution:
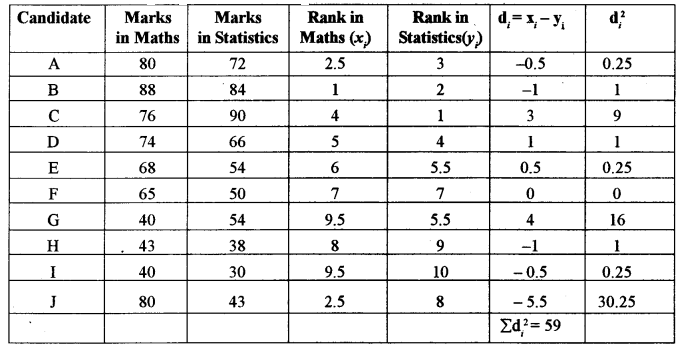
(a) In the case of Mathematics:
88 is scored by 1 student, so we assign rank 1 to it.
Again, 80 is scored by the two students So we assign common rank \(\frac{2+3}{2}=2.5\) to each of them.
And 76 is scored by only one thus we assign rank 4 to him.
74 is scored by only one, so we assign rank 5 to him.
68 is scored by only one so, we assign rank 6 to him.
65 is scored by only one so, we assign rank 7 to him.
43 is scored by only one so, we assign rank 8 to him.
40 is scored by two persons so, we assign common rank \(\frac{9+10}{2}=9.5\) to each of them.
In Statistics
90 is scored by only one thus we assign rank 1 to him.
84 is scored by only one thus we assign rank 2 to him.
72 is scored by only one thus we assign rank 3 to him.
66 is scored by only one thus we assign rank 4 to him.
54 is scored by two candidates thus we assign common rank \(\frac{5+6}{2}=5.5\) to both of them.
50 is scored by only one thus we assign rank 7 to him.
43 is scored by only one thus we assign rank 8 to him.
38 is scored by only one thus we assign rank 9 to him.
30 is scored by only one thus we assign rank 10 to him.

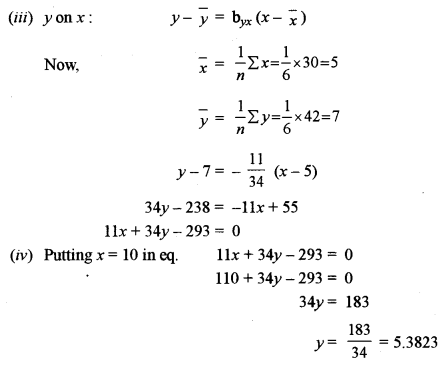
Question 8.
(a) A bag contains 8 red and 5 white balls. Two successive draws of 3 balls are made at random from the bag without replacements. Find the probability that the first draw yields 3 white balls and the second draw 3 red balls. [5]
(b) A box contains 30 bolts and 40 nuts. Half of the bolts and half of the nuts are rusted. If two items are drawn at random from the box, what is the probability that either both are rusted or both are bolts? [5]
Solution:
(a) A = Drawing 3 white balls in the first draw.
B = Drawing 3 red balls in the second draw.
Required Probability = P (A∩B) = P(A) . P(B/A)

Question 9.
(a) Using De Moivre’s theorem prove that: [5]

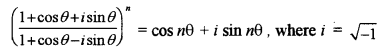
(b) Solve the differential equation: [5]

Solution:

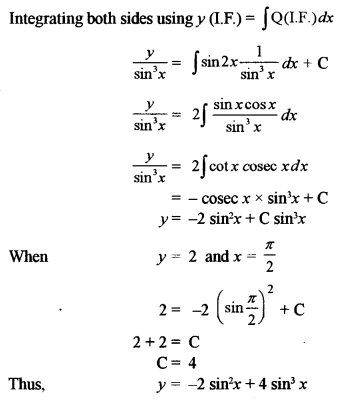
Section – B

Question 10.
(a) For any three vectors \(\vec{a}, \vec{b}, \vec{c}\) prove: [5]
\([\vec{a}-\vec{b} \quad \vec{b}-\vec{c} \quad \vec{c}-\vec{a}]=0\)
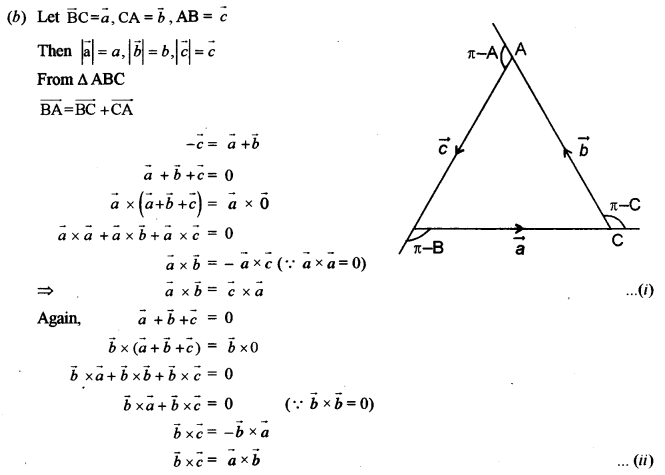
(b) In any triangle ABC, prove by vector method: [5]
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)
Solution:

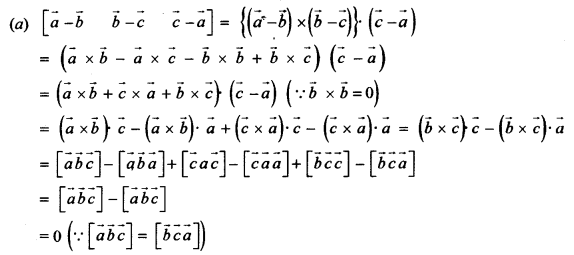
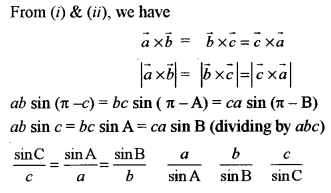
Question 11.
(a) Find the shortest distance between the lines: [5]

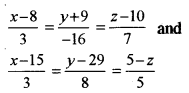
(b) Find the equation of the plane passing through the line of intersection of the planes x + 2y + 3z – 5 = 0 and 3x – 2y – z + 1 = 0 and cutting off equal intercepts on the x and z axes. [5]
Solution:

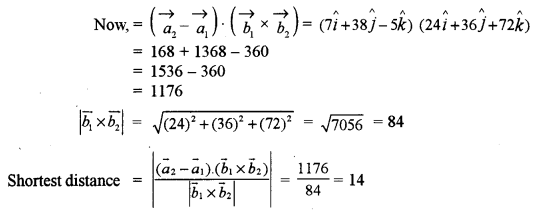
Question 12.
(a) In a class of 75 students, 15 are above average, 45 are average and the rest below-average achievers. The probability that an above-average achieving student fails is 0.005, that an average achieving student fails is 0.05 and the probability of a below-average achieving student failing is 0.15. If a student is known to have passed, what is the probability that he is a below-average achiever? [5]
(b) The probability that a bulb produced by a factory will fuse in 100 days of use is 0.05. Find the probability that out of 5 such bulbs, after 100 days of use: [5]
(i) None fuse.
(ii) Not more than one fuses.
(iii) More than one fuses.
(iv) At least one fuses.
Solution:
(a) Let E₁: event that student is above average
E₂: event that student is average
E₃: event that student is below average
A: event that student is known to have passed

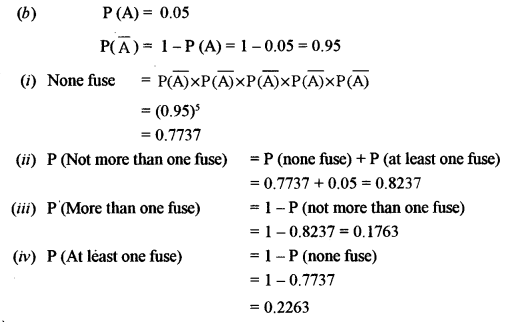
Section – C

Question 13.
(a) Two tailors P and Q earn ₹ 150 and ₹ 200 per day respectively. P and stitch 6 shirts and 4 trousers a day, while Q can stitch 10 shirts and 4 trousers per day. How many days should each work produce at least 60 shirts and 32 trousers at minimum labour cost? [5]
(b) A machine costs ₹ 97,000 and its effective life is estimated to be 12 years. If scrap realises ₹ 2,000 only, what amount should be retained out of profits at the end of each year to accumulate at compound interest of 5% per annum in order to buy a new machine after 12 years? (use 1.05¹² = 1.769). [5]
Solution:
(a) Let the tailor P work for x days and then tailor work for y days respectively.
Minimize Z = 150x + 200y
Subject to the constraints
6x + 10y ≥ 60
⇒ 3x + 5y ≥ 30 …..(i)
4x + 4y ≥ 32
⇒ x + y ≥ 8
and x ≥ 0, y ≥ 0
Solving eq. (i) and (ii), we have

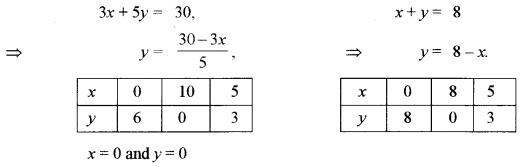
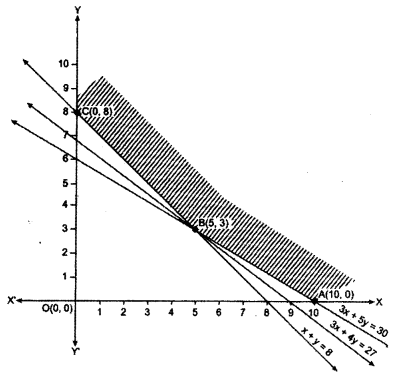
The lines are shown on the graph paper and the feasible region (Unbounded convex) is shown shaded in the fig.
The comer points are A (10, 0), B (5, 3) and C (0, 8)
At the comer point the value of Z = 150x + 200y
At A (10, 0), Z = 150 × 10 + 200 × 0 = 1500
At B (5, 3), Z = 150 × 5 + 200 × 3 = 750 + 600 = 1350
At C (0, 8), Z = 150 × 0 + 200 × 8 = 1600
As the feasible region is unbounded, we draw the graph of the half-plane
150x + 200y < 1350
3x + 4y < 27
There is no point common with the feasible region, therefore, Z has minimum value. Minimum value of Z is ₹ 1350 and it occurs at the point B (5, 3).
Hence, the labour cost in ₹ 1350 when P works for 5 days and Q works for 3 days.

(b) Cost = ₹ 97, 000
Scrap value = ₹ 2000
n = 12
\(i=\frac{5}{100}=0.05\)
Remaining amount = (97000 – 2000) = ₹ 95,000

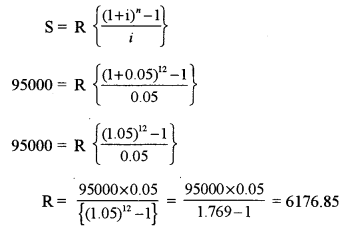
Question 14.
(a) Abill of ₹ 1,000 drawn on 7th May, 2011 for six months was discounted on 29th August, 2011 for cash payment of ₹ 988. Find the rate of interest charged by the bank.
(b) If total cost function is given by C = a + bx + cx², where x is the quantity of output. Show that:
\(\frac{d}{d x}(\mathrm{AC})=\frac{1}{x}(\mathrm{MC}-\mathrm{AC})\), where MC is the marginal cost and AC is the average cost.
Solution:
(a) Due date of the bill is 29th Nov.
Date of discounting is 29th Aug.
No. of days from date of discounting to due date
= 2(Aug) + 30 (Sept) + 31 (Oct) + 10 (Nov) = 73

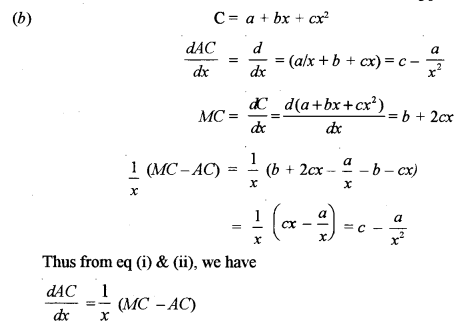
Question 15.
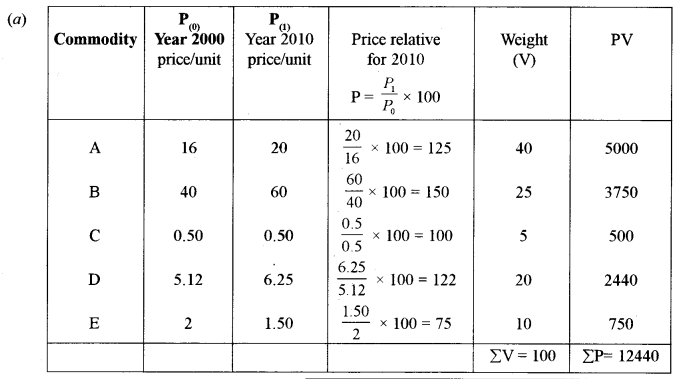
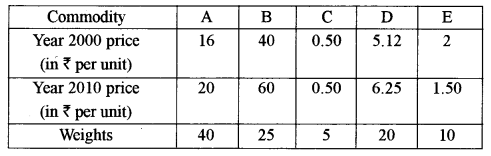
(a) Find the consumer price index number for the year 2010 using the year 2000 as the base year by using the method of weighted aggregates: [5]

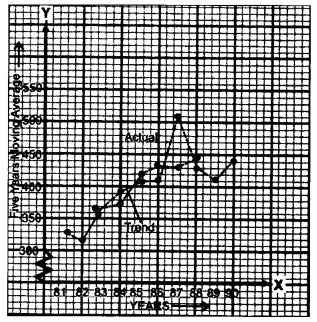
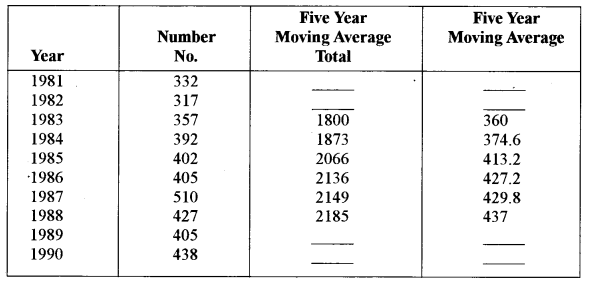
(b) Calculate the 5 yearly moving averages of the number of students in a college from the following data and plot them on a graph paper: [5]

Solution:

ISC Class 12 Maths Previous Year Question Papers