ISC Maths Question Paper 2011 Solved for Class 12

ISC Maths Previous Year Question Paper 2011 Solved for Class 12

Time Allowed: 3 Hours
Maximum Marks: 100

(Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.)

• The Question Paper consists of three sections A, B and C.
• Candidates are required to attempt all questions from Section A and all questions either from Section B or Section C.
• Section A: Internal choice has been provided in three questions of four marks each and two questions of six marks each.
• Section B: Internal choice has been provided in two questions of four marks each.
• Section C: Internal choice has been provided in two questions of four marks each.
• All working, including rough work, should be done on the same sheet as, and adjacent to the rest of the answer.
• The intended marks for questions or parts of questions are given in brackets [ ].
• Mathematical tables and graph papers are provided.

Section – A
(All questions are compulsory in this part)

Question 1.
(i) If \(A=\left[\begin{array}{ll}{3} & {-2} \\ {4} & {-2}\end{array}\right]\), find x such that A² = xA – 2I. Hence find A^-1. [3]
(ii) Find the values of k, if the equation 8x² – 16xy + ky² – 22x + 34y = 12 represents an elhpse. [3]
(iii) Solve for x: sin (2 tan^-1x) = 1 [3]
(iv) Two regression lines are represented by 2x + 3y – 10 = 0 and 4x + y – 5 = 0. Find the line of regression of y on x. [3]
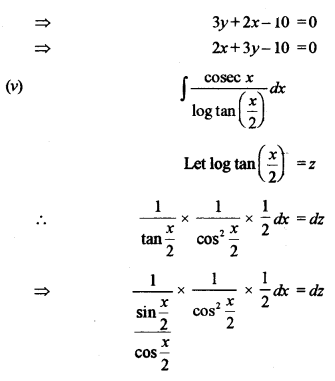
(v) Evaluate: [3]
\(\int \frac{\csc x}{\log \tan \left(\frac{x}{2}\right)} d x\)
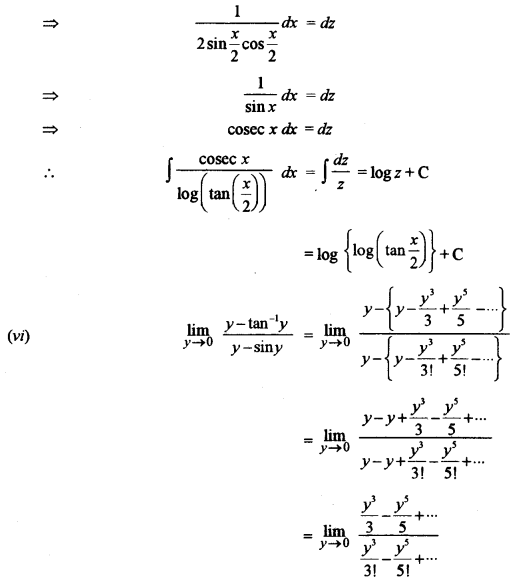
(vi) Evaluate: [3]
\(\lim _{y \rightarrow 0} \frac{y-\tan ^{-1} y}{y-\sin y}\)
(vii) Evaluate: [3]
\(\int_{0}^{1} \frac{x e^{x}}{(1+x)^{2}} d x\)
(viii) Find the modulus and argument of the complex number \(\frac{2+i}{4 i+(1+i)^{2}}\) [3]
(ix) A word consists of 9 different alphabets, in which there are 4 consonants and 5 vowels. Three alphabets are chosen at random. What is the probability that more than one vowel will be selected? [3]
(x) Solve the differential equation: [3]
\(\frac{d y}{d x}=e^{x+y}+x^{2} e^{y}\)
Answer:

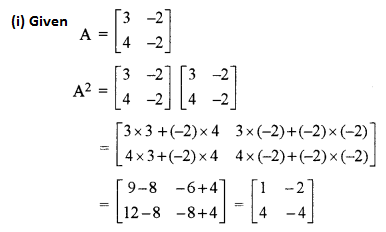
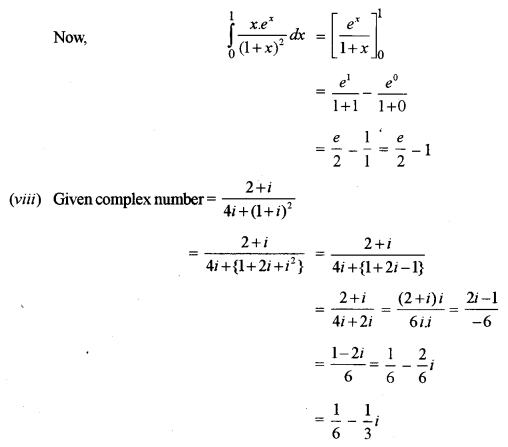
Question 2.
(a) Using properties of determinants, show that pα² + 2qα + r = 0, given that p, q and r are not in GP and [5]

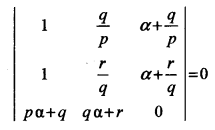
(b) Solve the following system of equations using matrix method: [5]

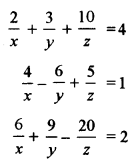
Answer:

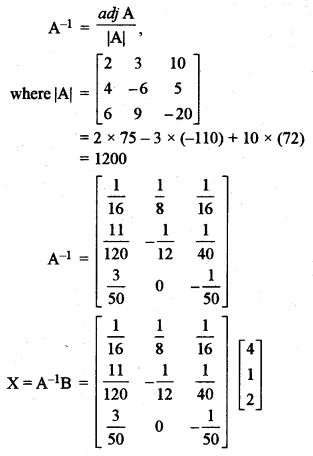
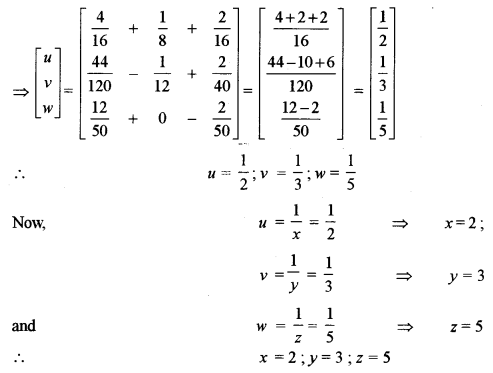
Question 3.
(a) Prove that: [5]
\(2 \tan ^{-1} \frac{1}{5}+\cos ^{-1} \frac{7}{5 \sqrt{2}}+2 \tan ^{-1} \frac{1}{8}=\frac{\pi}{4}\)
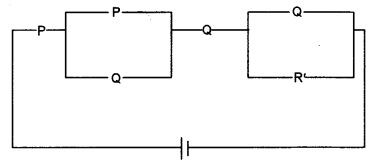
(b) P, Q and R represent switches in ‘ON position’ and P’, Q’ and R’ represent switches in ‘OFF position’. Construct a switching circuit representing the polynomial: [5]
P(P + Q)Q(Q + R’)
Use Boolean Algebra to show that the above circuit is equivalent to a switching circuit in which when P and Q are in ‘ON position’, the light is on.
Answer:


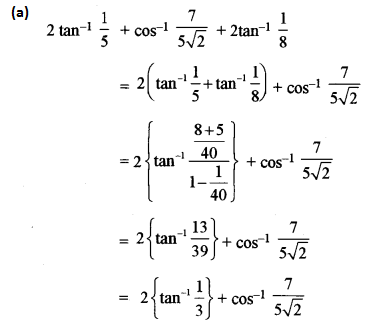
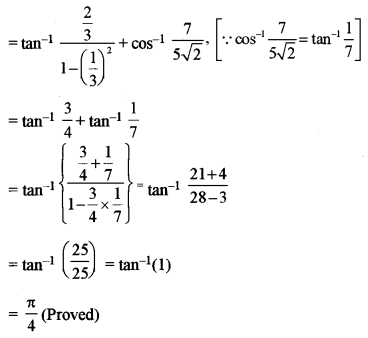
(b) P, Q, R represent switches in ON position and P’, Q’, R’ represent in OFF position.
Given polynomial is
P(P + Q) Q (Q + R’) = (PP + PQ) (QQ + QR’)
= (P + PQ) (Q + QR’)
= P(1 + Q)Q(1 + R’)
= P.1.Q.1
= PQ

Question 4.
(a) Verify Lagrange’s mean value theorem for the function f(x) = sin x – sin 2x in the interval [0, π]. [5]
(b) Find the equation of the hyperbola whose foci are (0, ±13) and the length of the conjugate axis is 20. [5]
Answer:

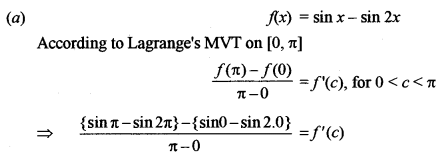
Question 5.
(a) Evaluate: [5]
\(\int \frac{x^{2}-5 x-1}{x^{4}+x^{2}+1} d x\)
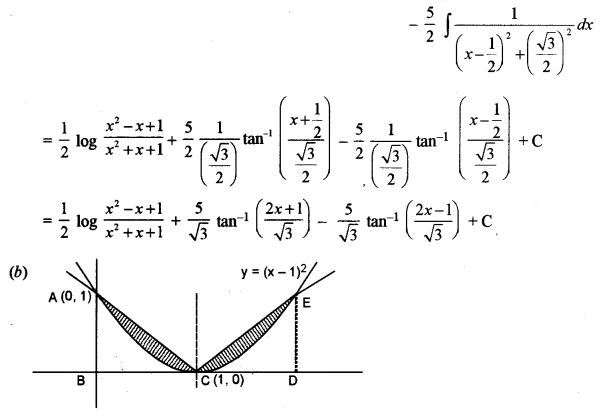
(b) Draw a rough sketch of the curves y = (x – 1)² and y = |x – 1|. Hence, find the area of the region bounded by these curves.
Answer:

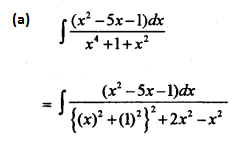
Question 6.
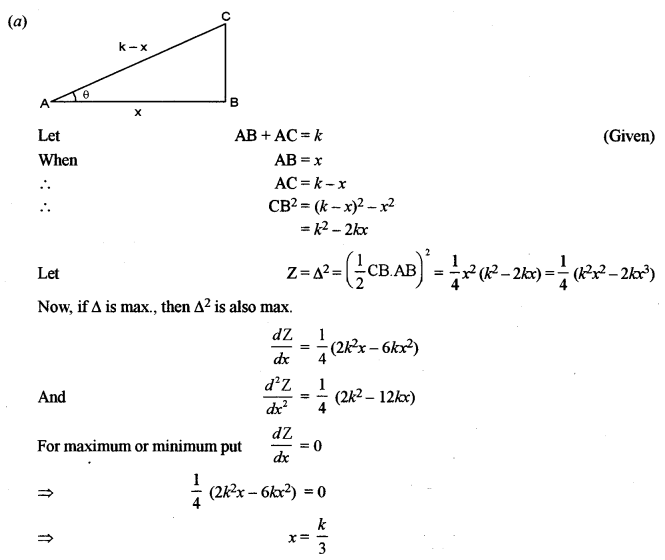
(a) If the sum of the lengths of the hypotenuse and a side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between them is \(\frac{\pi}{3}\) [5]
(b) If y = x^x, prove that: [5]
\(\frac{d^{2} y}{d x^{2}}-\frac{1}{y}\left(\frac{d y}{d x}\right)^{2}-\frac{y}{x}=0\)
Answer:

Question 7.
(a) The following observations are given:
(1, 4), (2, 8), (3, 2), (4, 12) (5, 10), (6, 14), (7, 16), (8, 6), (9, 18)
Estimate the value of y when the value of x is 10 and also estimate the value of x when the value of y = 5. [5]
(b) Compute Karl Pearson’s Coefficient of Correlation between sales and expenditures of a firm for six months. [5]

Answer:

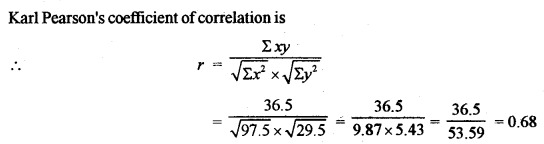
Question 8.
(a) A purse contains 4 silver and 5 copper coins. A second purse contains 3 silver and 7 copper coins. If a coin is taken out at random from one of the purses, what is the probability that it is a copper coin? [5]
(b) Aman arid Bhuvan throws a pair of dice alternately. In order to win, they have to get a sum of 8. Find their respective probabilities of winning if Aman starts the game. [5]
Answer:
(a) Let E₁ = selecting the first purse, E₂ selecting the second purse and A = coin drawn is silver.

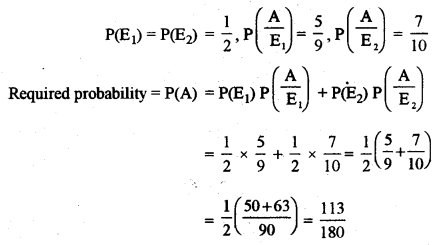
Question 9.
(a) Using De Moivre’s theorem, find the value of: [5]
\((1+i \sqrt{3})^{6}+(1-i \sqrt{3})^{6}\)
(b) Solve the following differential equation for a particular solution: [5]
\(y-x \frac{d y}{d x}=x+y \frac{d y}{d x}, \text { when } y=0 \text { and } x=1\)
Answer:

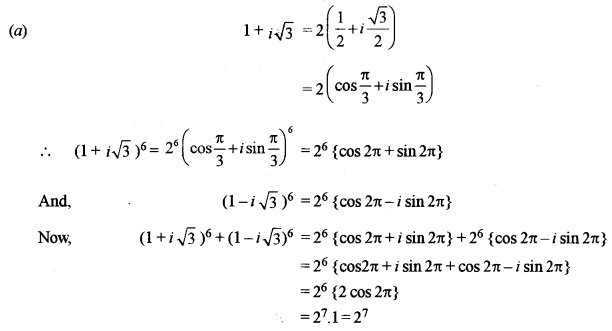
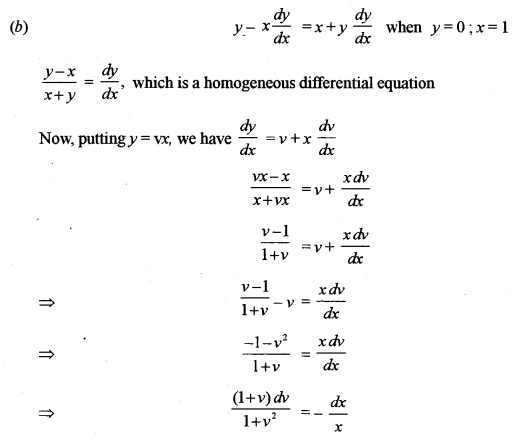
Section – B

Question 10
(a) Prove that: [5]
\([\vec{a}+\vec{b} \vec{b}+\vec{c} \vec{c}+\vec{a}]=2[\vec{a} \vec{b} \vec{c}]\)
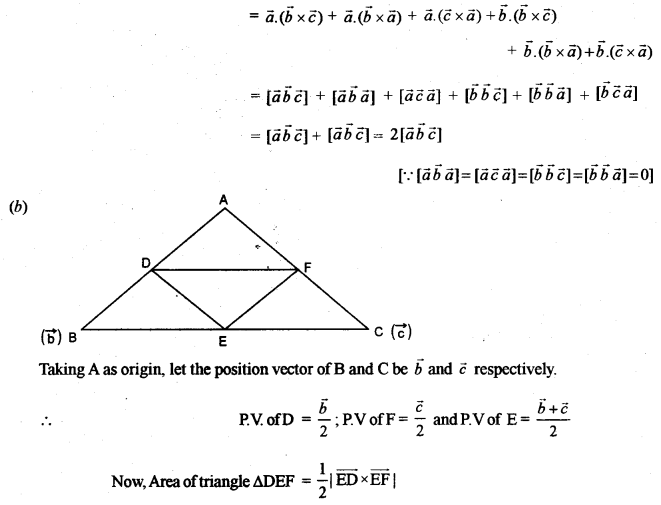
(b) If D, E, F are mid-points of the sides of a triangle ABC, prove by vector method that:
Area of ∆DEF = \(\frac { 1 }{ 4 }\) (Area of ∆ABC). [5]
Answer:

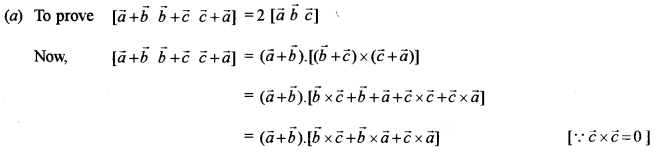
Question 11.
(a) Find the vector equation of the line passing through the point (-1, 2, 1) and parallel to the line \(\vec{r}=2 \hat{i}+3 \hat{j}-\hat{k}+\lambda(\vec{i}-2 \hat{j}+\hat{k})\). Also, find the distance between these lines. [5]
(b) Find the equation of the plane passing through the points A (2, 1, -3), B (-3, -2, 1) and C(2, 4, -1). [5]
Answer:
(a) \(\vec{r}=2 \hat{i}+3 \hat{j}-\hat{k}+\lambda(\vec{i}-2 \hat{j}+\hat{k})\) …(i)
The given fine is parallel to the vector \(\hat{i}-2 \hat{j}+\hat{k}\) and the required line is parallel to given line So, required line is parallel to the vector \(\hat{i}-2 \hat{j}+\hat{k}\)
It is given that the required line passes through the point (-1, 2, 1)
The equation of the required line is

(b) Let the equation of the plane passing through the point A(2, 1, -3) be
A (x – 2) + B(y – 1) + C(z + 3) = 0 ….. (i)
Points B (-3, -2,1) and C (2, 4, -1) lies on the plane.
⇒ A(-3 – 2) + B (-2 – 1) + C(1 + 3) = 0
⇒ -5A – 3B + 4C = 0 ……(ii)
And A(2 – 2) + B(4 – 1) + C(-1 + 3) = 0
⇒ A.0 + 3B + 2C = 0 ….(iii)
Now, eliminating A, B, C from (i), (ii) and (iii), we have

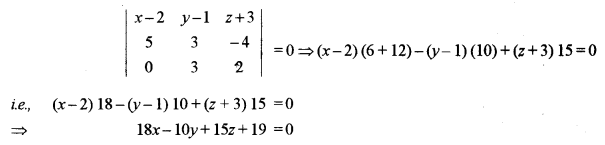
Question 12.
(a) A box contains 4 red and 5 black marbles. Find the probability distribution of the red marbles in a random draw of three marbles. Also find the mean and standard deviation of the distribution. [5]
(b) Bag A contains 2 white, 1 black and 3 red balls, Bag B contains 3 white, 2 black and 4 red balls and Bag C contains 4 white, 3 black and 2 red balls. One Bag is chosen at random and 2 balls are drawn at random from that Bag. If the randomly drawn balls happen to be red and black, what is the probability that both balls come from Bag B? [5]
Answer:
(a) The box contains 4 red and 5 black marbles
3 marbles are drawn.
Probability of one red marble drawn is

(b) Let E₁, E₂ and E₃ the following events
E₁ = Bag A chosen; E₂ = Bag B chosen; E₃ = Bag C chosen.
\(P\left(E_{1}\right)=P\left(E_{2}\right)=P\left(E_{3}\right)=\frac{1}{3}\)
Now, the probability of drawing a red and a black ball from bag A is,

Section – C

Question 13.
(a) The price of a tape recorder is ₹ 1,661. A person purchases it by making a cash payment of ₹ 400 and agrees to pay the balance with due interest in 3 half-yearly equal instalments. If the dealer charged interest at the rate of 10% per annum compounded half-yearly, find the value of the instalment. [5]
(b) A manufacturer manufactures two types of tea-cups, A and B. Three machines are needed for manufacturing the tea-cups. The time in minutes required for manufacturing each cup on the machines is given below:

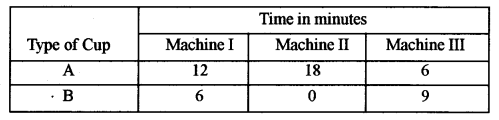
Each machine is available for a maximum of six hours per day. If the profit on each cup of type A is ₹ 1.50 and that on each cup of type B is ₹ 1.00, find the number of cups of each type that should be manufactured in a day to get maximum profit. [5]
Answer:
(a) The price of a tape recorder is ₹ 1661.
The man purchases it by ₹ 400 cash down payment.
Due amount = 1661 – 400 = ₹ 1261

Question 14.
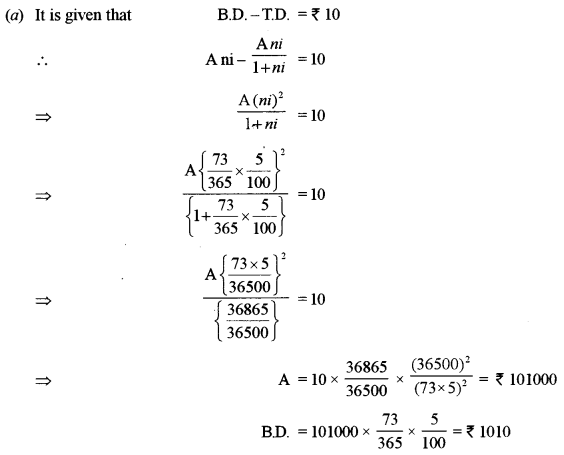
(a) If the difference between Banker’s discount and True discount of a bill for 73 days at 5% per annum is ₹ 10, find
(i) the amount of the bill
(ii) Banker’s discount. [5]
(b) Given that the total cost function for x units of a commodity is: [5]
\(C(x)=\frac{x^{3}}{3}+3 x^{2}-7 x+16\)
(i) Find the Marginal Cost (MC)
(ii) Find the Average Cost (AC)
(iii) Prove that: Marginal Average Cost (MAC) = \(\frac{x(MC)-C(x)}{x^{2}}\)
Answer:

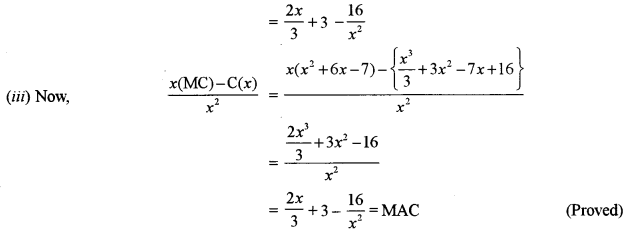
Question 15.
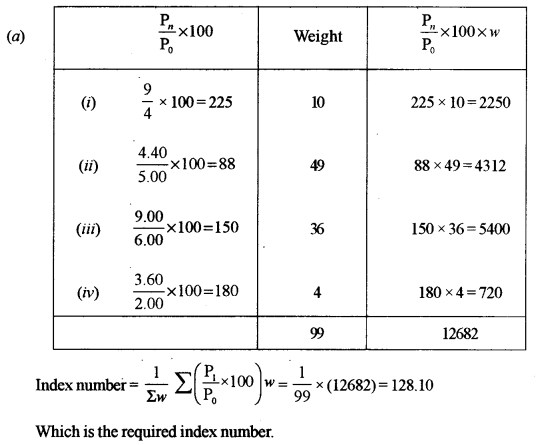
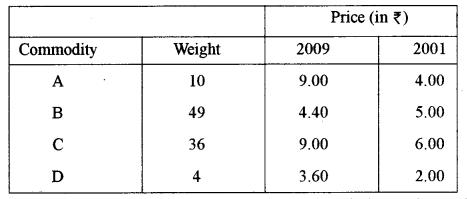
(a) The price quotations of four different commodities for 2001 and 2009 are as given below. Calculate the index number for 2009 with 2001 as the base year by using a weighted average of price relative method.

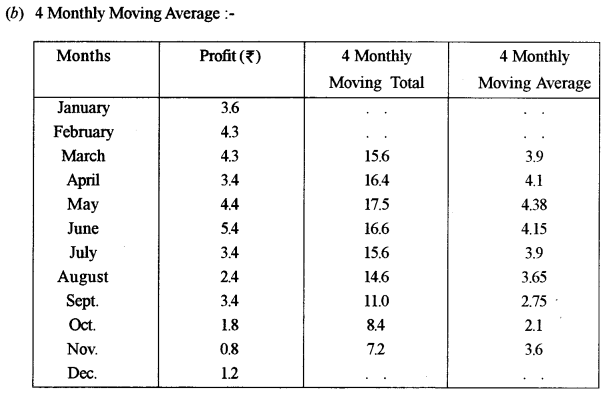
(b) The profit Of a soft drink firm (in thousands of ₹) during each month of the year is as given below:

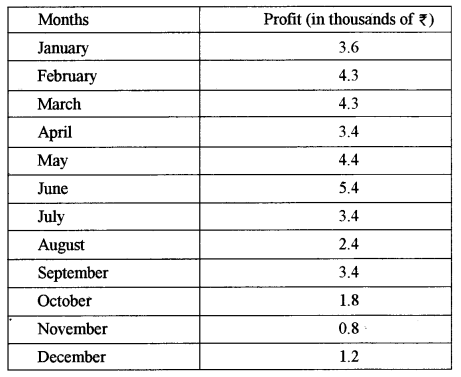
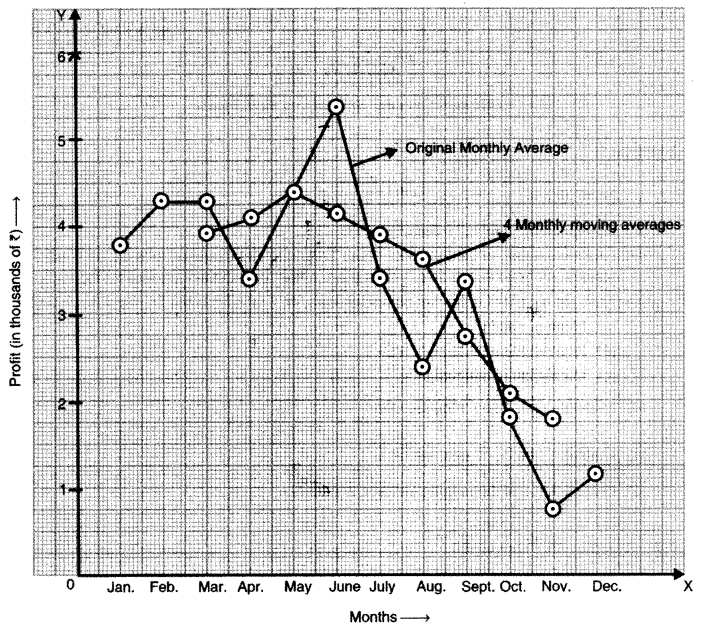
Calculate four monthly moving averages and plot these and the original data on a graph sheet.
Answer:

ISC Class 12 Maths Previous Year Question Papers