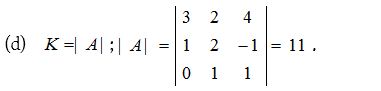Inverse of a Matrix using Minors, Cofactors and Adjugate

Inverse of a Matrix using Minors, Cofactors and Adjugate

Minors and Cofactors

Minor of an element:
If we take the element of the determinant and delete (remove) the row and column containing that element, the determinant left is called the minor of that element. It is denoted by M_ij.

Similarly, we can find the minors of other elements. Using this concept the value of determinant can be
∆ = a₁₁M₁₁ – a₁₂M₁₂ + a₁₃M₁₃
or, ∆ = – a₂₁M₂₁ + a₂₂M₂₂ – a₂₃M₂₃
or, ∆ = a₃₁M₃₁ – a₃₂M₃₂ + a₃₃M₃₃

Cofactor of an element:
The cofactor of an element a_ij (i.e. the element in the i^th row and j^th column) is defined as (–1)^i+j times the minor of that element. It is denoted by C_ij or A_{ij or} F_ij.
C_ij = (–1)^i+j M_ij.

where C₁₁ = (–1)¹⁺¹ M₁₁ = +M₁₁ , C₁₂ = (–1)¹⁺² M₁₂ = –M₁₂ and C₁₃ = (–1)¹⁺³ M₁₃ = +M₁₃
Similarly, we can find the cofactors of other elements.

Adjugate (also called Adjoint) of a Square Matrix

Let A = [a_ij] be a square matrix of order n and let C_ij be cofactor a_ij of in A. Then the transpose of the matrix of cofactors of elements of A is called the adjoint of A and is denoted by adj A
Thus, adj A = [C_ij]^T ⇒ (adj A)_ij = C_ji = cofactor of a_ij in A.

Properties of adjoint matrix:
If A, B are square matrices of order n and is corresponding unit matrix, then

1. A(adj A)=|A|, I_n =(adj A)A
   (Thus A (adj A) is always a scalar matrix)
2. |adj A|= |A|^n-1
3. adj(adj A) = |A|^n-2 A
4. adj(adj A) =|A|^{(n-1)^2}
5. adj(A^T) = (adj A)^T
6. adj(AB) = (adj B)(adj A)
7. adj(A^m) = (adj A)^m, m ∈ N
8. adj(kA) = k^n-1(adj A), k ∈ R
9. adj(I_n) = I_n
10. adj(0) = 0
11. A is symmetric ⇒ adj A is also symmetric.
12. A is diagonal ⇒ adj A is also diagonal.
13. A is triangular ⇒ adj A is also triangular.
14. A is singular ⇒ |adj A|= 0

Adjoint of a Square Matrix Problems with Solutions

1.

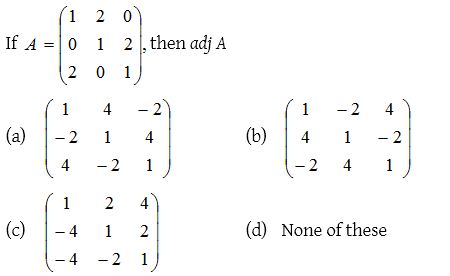
Solution:

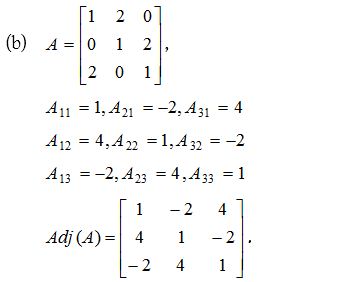
2.

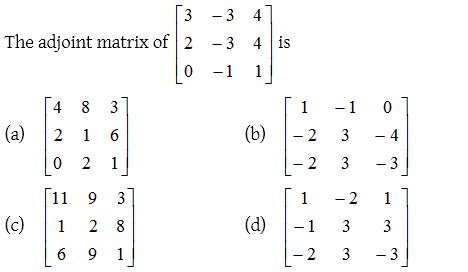
Solution:

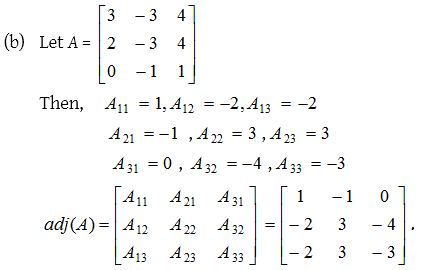
Inverse of a Matrix

A non-singular square matrix of order n is invertible if there exists a square matrix B of the same order such that AB = I_n =BA .
In such a case, we say that the inverse of A is B and we write A^-1 = B. The inverse of A is given by

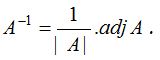
The necessary and sufficient condition for the existence of the inverse of a square matrix A is that |A| ≠ 0.

Properties of inverse matrix:
If A and B are invertible matrices of the same order, then

1. (A^-1)^-1 = A
2. (A^T) ^-1 =(A^-1)^T
3. (AB) ^-1 = B^-1A^-1
4. (A^k)^-1 = (A^-1)^k, k ∈ N [In particular (A²)^-1 =(A^-1)²]
5. adj(A^-1) = (adj A)^-1
6. 
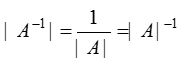
7. A = diag (a₁a₂…a_n) ⇒ A^-1 = diag(a₁^-1a₂^-1…a_n^-1)
8. A is symmetric ⇒ A^-1 is also symmetric.
9. A is diagonal, |A| ≠ 0 ⇒ A^-1 is also diagonal.
10. A is a scalar matrix ⇒ A^-1 is also a scalar matrix.
11. A is triangular, |A| ≠ 0 ⇒ A^-1 is also triangular.
12. Every invertible matrix possesses a unique inverse.
13. Cancellation law with respect to multiplication.
    If A is a non-singular matrix i.e., if |A|≠ 0 ,then A^-1 exists and AB = AC ⇒ A^-1(AB) = A^-1(AC)
    ⇒ (A^-1A)B =(A^-1A)C
    ⇒ IB = IC ⇒ B=C
    ∴ AB=AC ⇒ B = C ⇔|A|≠ 0.

Inverse of a Matrix Problems with Solutions

1.

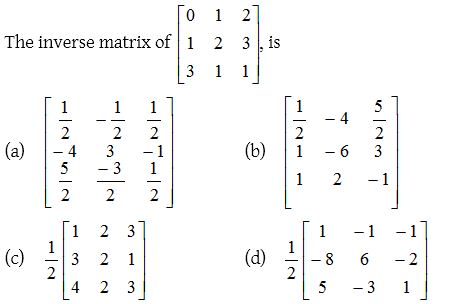
Solution:

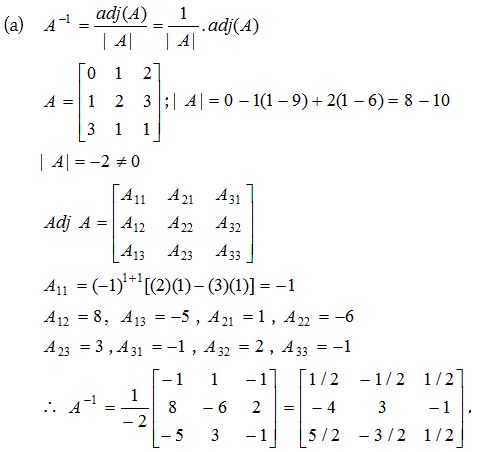
2.

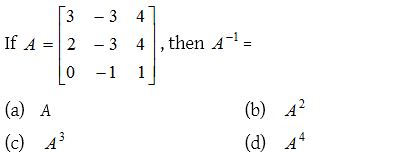
Solution:

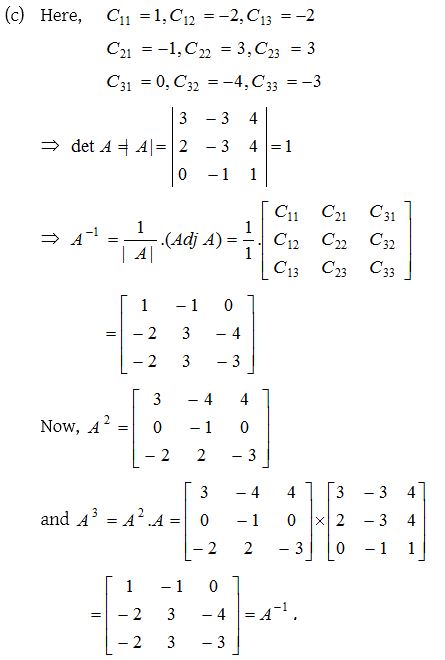
3.

Solution: